Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc

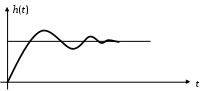
Рис. 16. Переходная характеристика колебательного звена

Если   0, то получаем колебательное звено.

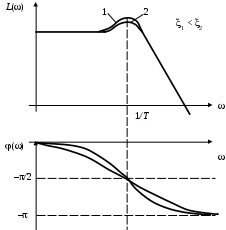
ЛАЧХ и ЛФЧХ колебательного звена представляют собой семейство кривых (рис. 17), где  выступает как параметр.

Увеличение логарифмической характеристики в области сопрягающей частоты имеет место, если  < 0,707.

Предельный случай – это консервативное звено  = 0. При этом передаточная функция имеет вид

.



а)

б)

Рис. 17. Частотные характеристики колебательного звена

а) ЛАЧХ; б) ЛФЧХ

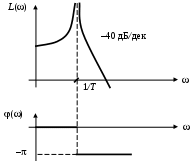
Логарифмические характеристики представлены на рис. 18.


а)

б)

Рис. 18. Частотные характеристики консервативного звена

а) ЛАЧХ; б) ЛФЧХ

5. Интегрирующее звено.

ДУ звена имеет вид .

Передаточная функция равна .

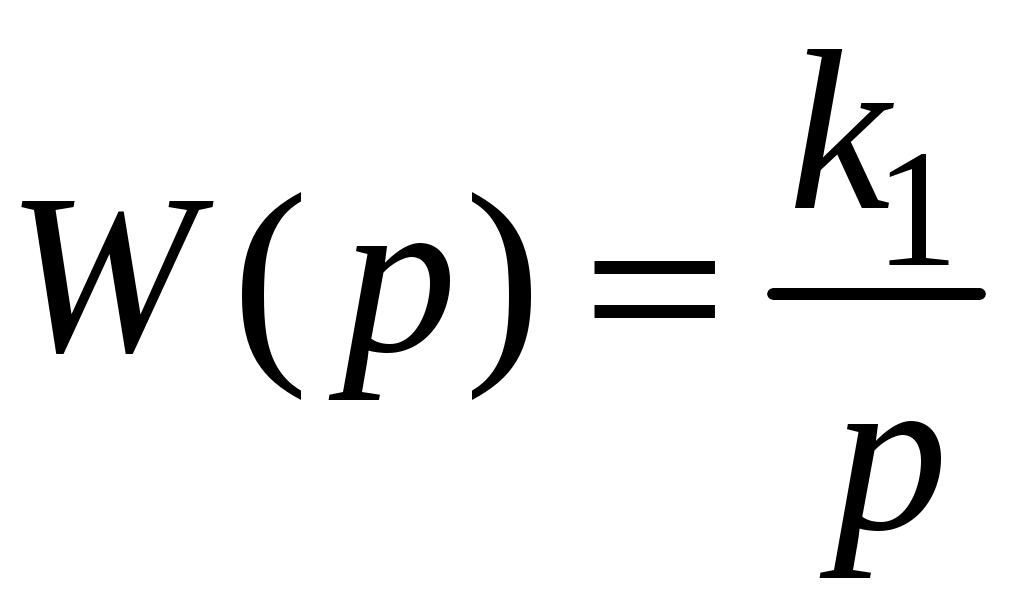Графики весовой функции (t) =k₁ и переходной характеристики h(t) = k₁t представлены на рис. 19.




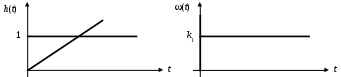
а) б)

Рис. 19. Интегрирующее звено

а) переходная характеристика; б) весовая функция

Анализ графиков показывает, что звено является неустойчивым, т. к. при ограниченном входном воздействии 1(t) выходной сигнал неограниченно нарастает.

Частотные характеристики представлены на рис.20.



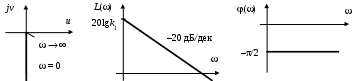
а) б) в)

Рис. 20. Частотные характеристики интегрирующего звена

а) годограф; б) ЛАЧХ; в) ЛФЧХ

;

.

6. Дифференцирующее звено.

Звено описывается следующими соотношениями

;

;

---

;



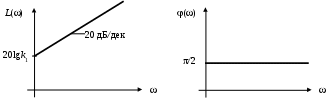
Логарифмические характеристики представлены на рис. 21.


а) б)

Рис. 21. Частотные характеристики дифференцирующего звена

а) ЛАЧХ; б) ЛФЧХ

---

6. Построение передаточных функций САУ

Анализ САУ с помощью передаточных функций начинается с построения структурной схемы.

Структурная схема – это изображение звеньев со связями между ними. Для звеньев указываются их передаточные функции. В теории САУ существует три вида соединения звеньев.

1. Последовательное.

С 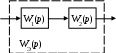труктурная схема такого соединения представлена на рис. 22.
Рис. 22. Последовательное соединение звеньев САУ

Если при соединении звеньев не изменяется ДУ каждого звена, то эквивалентная передаточная функция равна

W_Э(p) = W₁(p)W₂(p).

2. Параллельное.

Структурная схема такого соединения имеет вид (рис. 23).

W_Э(p) = W₁(p) + W₂(p).



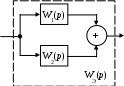
Рис 23. Параллельное соединение звеньев САУ

3. Обратная связь.

Такое соединение имеет следующую структурную схему (рис. 24).



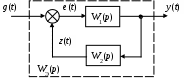
Рис. 24. Соединение в виде обратной связи

Получить выражение для W_Э(p) можно из следующих соотношений:

e(t) = g(t)  z(t);

z(t) = y(t)  W₂(p);

y(t) = e(t)  W₁(p);

.

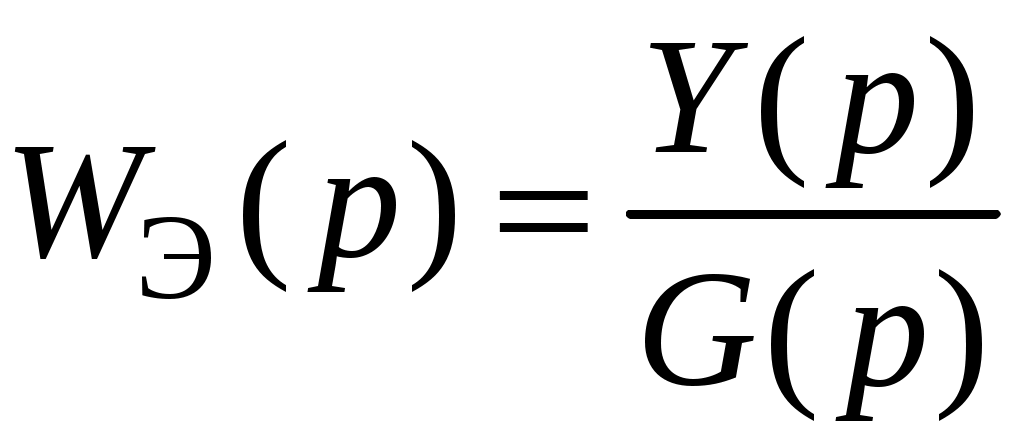Получим .

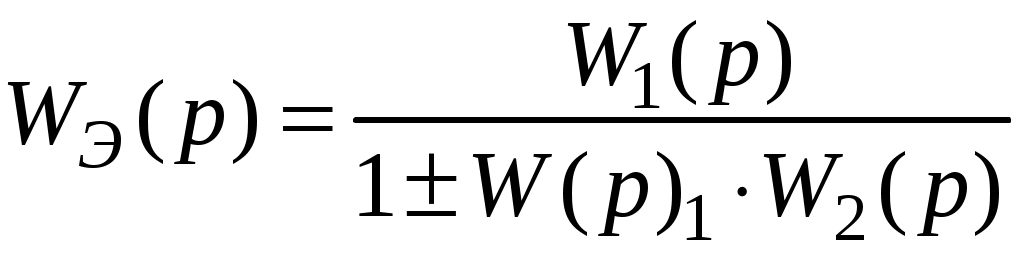Существуют определенные правила преобразования структурных схем. Основное условие заключается в том, чтобы обеспечить неизменность действия сигналов в эквивалентных точках структурной схемы.

1. Перенос сумматора (рис. 25).

2. Перенос узла (рис. 26).


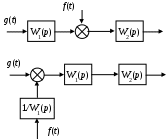
Рис. 25. Перенос сумматора в структурной схеме САУ



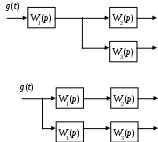
Рис. 26. Перенос узла в структурной схеме САУ

7. Составление исходных дифференциальных
уравнений САУ

---

Как уже отмечалось выше, ДУ получаются на основании физической природы объекта. Затем при необходимости производится их линеаризация.

При этом к системе могут быть приложены некоторые воздействия:

1) задающее воздействиеg(t), которое определяет требуемый закон изменения выходной величины;

2) возмущающее воздействие f(t).

Если действуют несколько входных сигналов, то используется принцип суперпозиции.

ДУ можно составить как относительно выходной регулируемой величины, так и относительно сигнала ошибкиx(t).

Дифференциальное уравнение относительно ошибки в общем виде имеет следующий вид.

,

где D(p), Q(p), P(p) – полиномы, причем D называется характеристическим полиномом.

;

. (2)

Структурная схема САУ при этом имеет следующий вид (рис. 27), сопоставимый с видом САУ, описанным в разделе Основные понятия и определения (см. рис. 1).




Рис. 27. Структура САУ

ПУ – преобразующее устройство;

ИЭ – исполнительный элемент;

РО – регулируемый объект;

u(t) – регулирующее (управляющее) воздействие.

Рассмотрим первоначально разомкнутую (без обратной связи) САУ. Математические соотношения при этом имеют вид:

;

,

гдеW₀(р) – передаточная функция по регулирующему воздействию u(t);

W_f(р) – передаточная функция по возмущающему воздействию.

В теории САУ широко используется понятие передаточной функции разомкнутой системы:

---

;

.

Рассмотрим замкнутую систему. Для этого нужно использовать уравнение замыкания (2). Выражение для выходного сигнала в этом случае будет иметь вид:

,

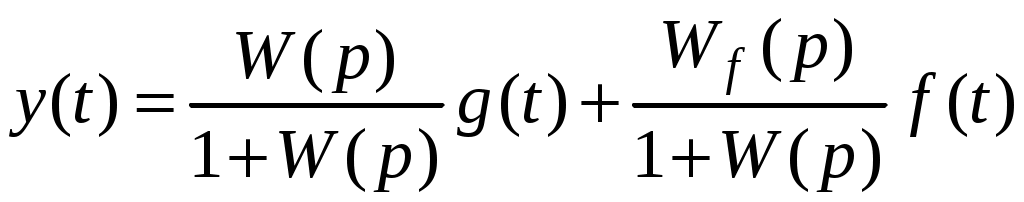а для ошибки САУ:

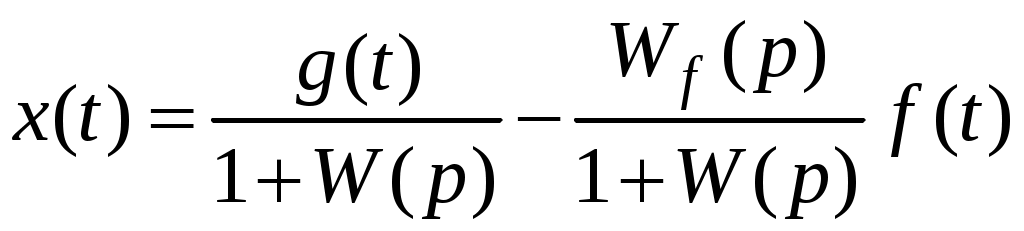, (3)

Анализ двух последних выражений позволяет определить следующие виды передаточных функций замкнутой САУ:

1) 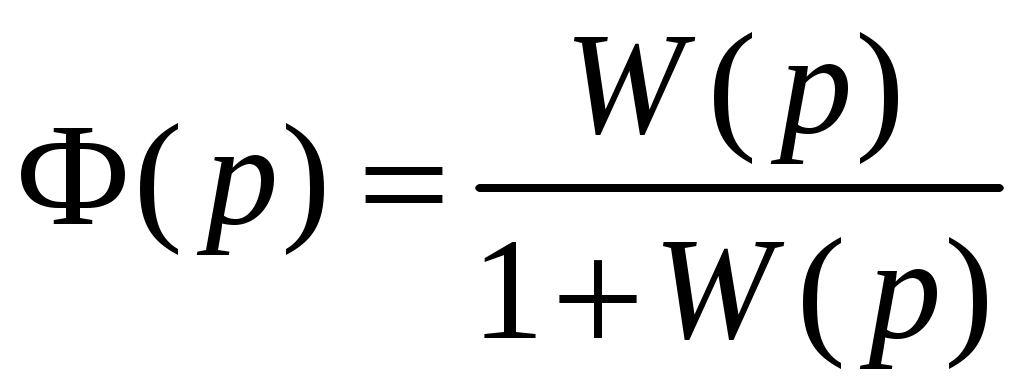– передаточная функция замкнутой системы;

2) 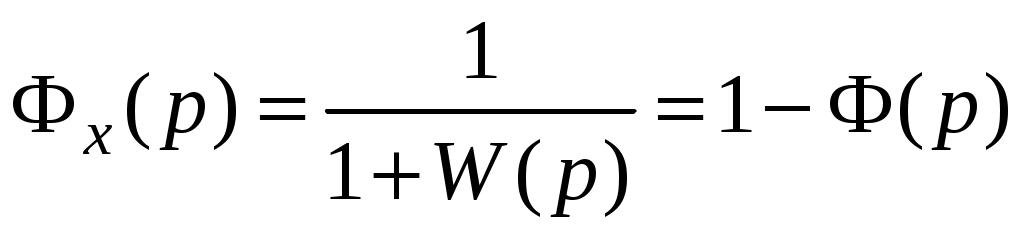– передаточная функция замкнутой системы по ошибке.

Эти функции можно представить и через изображения сигналов, поступающих и проходящих через САУ , .

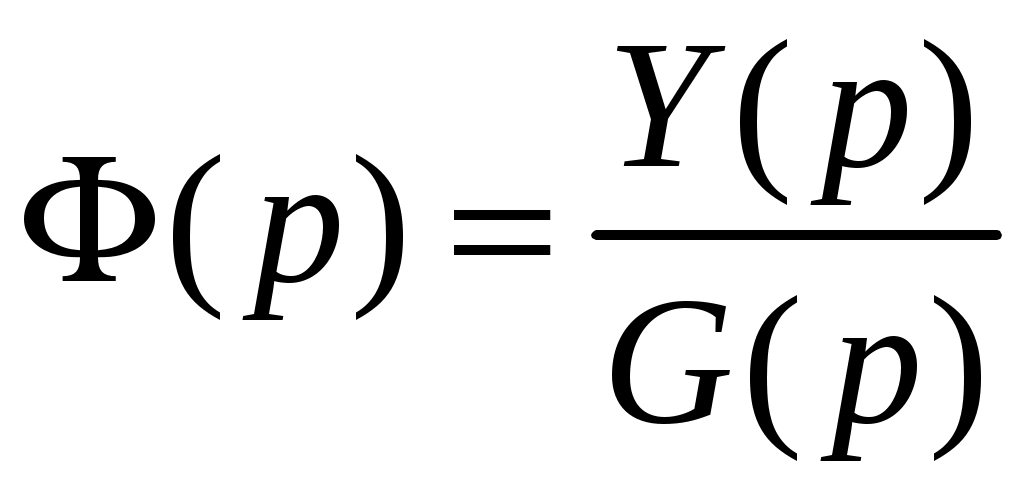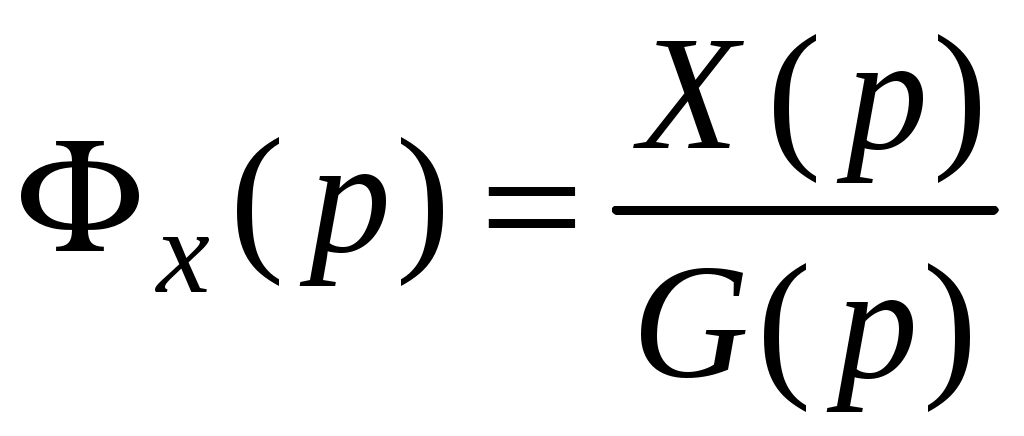Передаточную функцию разомкнутой системы можно представить в виде дробно-рациональной функции.

Характеристический полином D(p) может быть найден как знаменатель передаточной функции замкнутой системы 1 + W(p).

Важное значение в теории САУ имеет характеристическое
уравнение

D(p) = 0; 1 + W(p) = 0.

---