Файл: Курс лекций по дисциплине Эконометрика.doc

Часто эконометрист сталкивается с ситуацией, когда к уже имеющейся выборке он хочет присоединить небольшую дополнительную порцию данных, но не знает, можно ли считать выборки регрессионно однородными.

Если необходимо выяснить, можно ли использовать одну и ту же модель для двух разных выборок данных или следует оценивать отдельные регрессии для каждой выборки, то можно воспользоваться тестом Чоу.

Рассмотрим модели:

(4.14)

(4.15)

Мы хотим проверить гипотезу

H₀: ,

которая содержательно означает, что для двух имеющихся выборок из n₁ и n₂ наблюдений можно использовать одну и ту же регрессионную модель, т.е. выборки можно объединить.

Процедура Чоу для статистической проверки гипотезы H₀ суть:

1. Строим МНК оценки регрессии (4.14) и вычисляем сумму квадратов остатков, которую обозначим . Строим МНК оценки регрессии (4.15) и вычисляем сумму квадратов остатков, которую обозначим .

2. Строим МНК оценки регрессии по объединенной (общей) выборке, содержащей в себе все наблюдения (числом n₁+n₂) обеих выборок и вычисляем сумму квадратов остатков, которую обозначим e_r.

3. Критическая статистика F вычисляется по формуле:



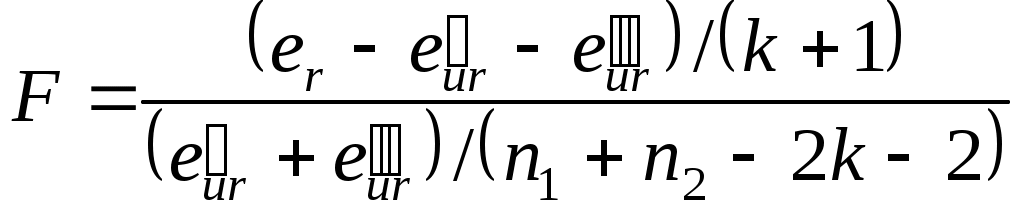
и имеет распределение Фишера с (k+1) и (n₁+n₂2k2) степенями свободы. Если F > F_, то нулевая гипотеза отвергается, и в этом случае мы не можем объединить две выборки в одну.
5. Временные ряды
5.1.Специфика временных рядов

---

Часто исследователь имеет дело с данными в виде временных рядов.

Совокупность наблюдений анализируемой величины , произведенных в последовательные моменты времени , называется временным рядом.

Иначе говоря, временной ряд – это упорядоченная во времени последовательность наблюдений.

Среди временных рядов выделяют одномерные, полученные в результате наблюдения одной, фиксированной характеристики исследуемого объекта, и, многомерные временные ряды как результат наблюдений нескольких характеристик одного исследуемого объекта в течение ряда моментов времени.

По времени наблюдения временные ряды делятся на дискретные и непрерывные. Дискретные ряды, в свою очередь, разделяются на ряды с равноотстоящими и произвольными моментами наблюдения.

Временные ряды бывают детерминированными и случайными: первые получены как значения некоторой неслучайной функции, а вторые - как реализации случайной величины.

Стохастические временные ряды подразделяются на стационарные и нестационарные. Ряд y(t) называется стационарным (в узком смысле), если среднее, дисперсия и ковариации y(t) не зависят от t.

В дальнейшем, если не оговорено иначе, будем рассматривать одномерные, дискретные с равноотстоящими моментами наблюдений случайные временные ряды.

Природа временных рядов существенно отличается от природы пространственных данных, что проявляется в весьма специфических свойствах временных рядов. В своей работе исследователь должен учитывать эти особенности, основные из которых отображены в таблице 5.1.

Таблица 5.1

Особенности временных рядов

Характеристики наблюдений	Тип данных
	Пространственные данные	Временные ряды
Порядок	Не существенен	Существенен
Статистическая независимость	Независимы	Не являются статистически независимыми
Функция распределения	Распределены одинаково	Распределены неодинаково
Количество	Как правило, большое	Как правило, небольшое
Наличие автокорреляции	Встречается нечасто	Встречается часто

---

Значения элементов временного ряда формируются под воздействием ряда факторов, среди которых выделяют:

• 
  долговременные, формирующие в длительной перспективе общую тенденцию анализируемого признака. Эта тенденция описывается с помощью некоторой функции, называемой трендом (Т);
  
• 
  сезонные, формирующие периодически повторяемые в определенное время года колебания анализируемого признака (S);
  
• 
  циклические, формирующие изменения анализируемого в результате воздействия циклов экономической, демографической или астрофизической природы (С);
  
• 
  случайные, не поддающиеся учету и регистрации, как результат воздействия случайных, внешних факторов (U).
  

Первые три составляющие часто объединяют в одну детерминированную и рассматривают модель ряда в виде y_t=f(t)+u_t, t. Изменение уровня f(t) со временем называют при этом трендом.

Предметом анализа временного ряда является выделение и изучение указанных компонент ряда, как правило в рамках одной из моделей ряда: либо аддитивной Y=T+C+S+U, либо мультипликативной Y=TCSU.

Некоторые составляющие могут отсутствовать в тех или иных рядах.

В результате анализа временного ряда необходимо определить, какие из неслучайных составляющих присутствуют в разложении ряда, построить для них хорошие оценки, подобрать модель, описывающую поведение остатков и оценить ее параметры.
5.2. Проверка гипотезы о существовании тренда
Для выявления факта наличия или отсутствия неслучайной составляющей f(t), то есть для проверки гипотезы о существовании тренда - Н₀: Еy(t)=a=const, используют следующие критерии.

I. Критерий серий. Упорядочим члены ряда по возрастанию: y₁, y₂, ..., y_t, ..., y_n. Определим медиану ряда:



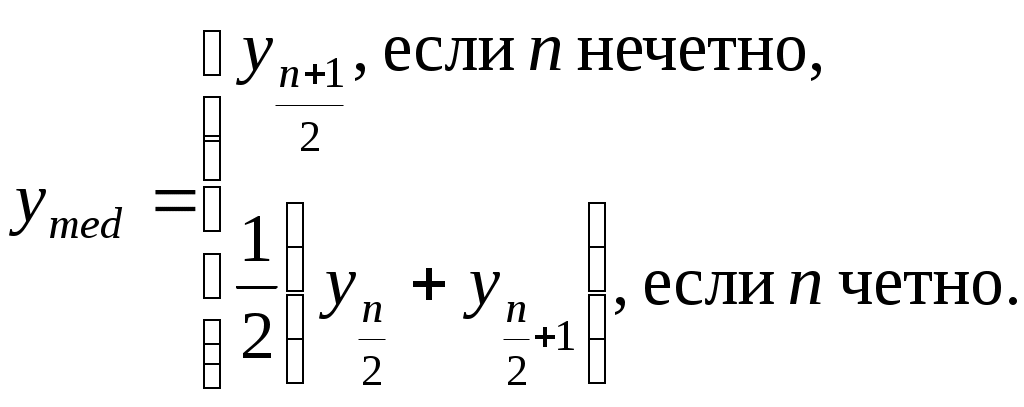
Образуем последовательность плюсов и минусов, соответствующую исходному ряду, по правилу: если y_t>y_med, то y_t соответствует плюс, если y_t<y_med, то – минус. Под серией понимается последовательность подряд идущих плюсов и подряд идущих минусов. Подсчитаем общее число серий  и протяженность самой длинной серии .

---

Если хотя бы одно из неравенств:



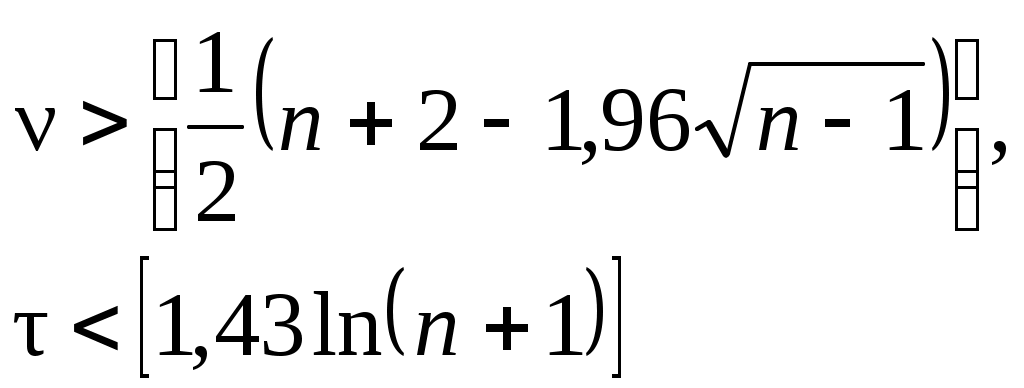
окажется нарушенным, то гипотеза Н₀ отвергается с вероятностью ошибки , заключенной между 0,05 и 0,0975.

II. Критерий "восходящих" и "нисходящих" серий. Аналогично предыдущему критерию исследуется последовательность плюсов и минусов. Правило построения последовательности: если y_t+1-y_t>0, то y_t соответствует плюс, если y_t+1-y_t<0, то – минус (если подряд идут несколько равных наблюдений, то во внимание принимается одно из них).

Если хотя бы одно из неравенств:



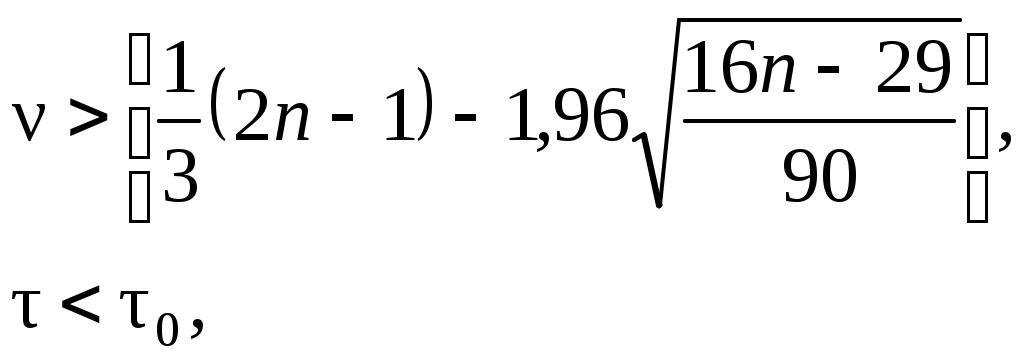
окажется нарушенным, то гипотеза Н₀ отвергается с вероятностью ошибки , заключенной между 0,05 и 0,0975. Величина ₀ определяется в зависимости от n:

n	n26	26<n153	153<n1170
0	0=5	0=6	0=7

III. Критерий квадратов последовательных разностей (критерий Аббе). Если есть основания полагать, что разброс наблюдений y_t относительно своих средних значений подчиняется нормальному закону распределения вероятностей, то применяется критерий Аббе - см. [1], с. 801-802.
5.3. Аналитическое выравнивание временных рядов, оценка параметров уравнения тренда
Метод обработки временных рядов, целями которого является устранение случайных колебаний и построение аналитической функции, характеризующей зависимость уровней ряда от времени – тренда, называется аналитическим выравниванием временного ряда.

Суть метода аналитического выравнивания состоит в том, чтобы заменить фактические уровни временного ряда на теоретические . Расчет осуществляется по некоторому формализованному уравнению, принятому за математическую модель тренда. Для построения трендов чаще всего применяют такие функции, как:

---

• 
  линейная: ;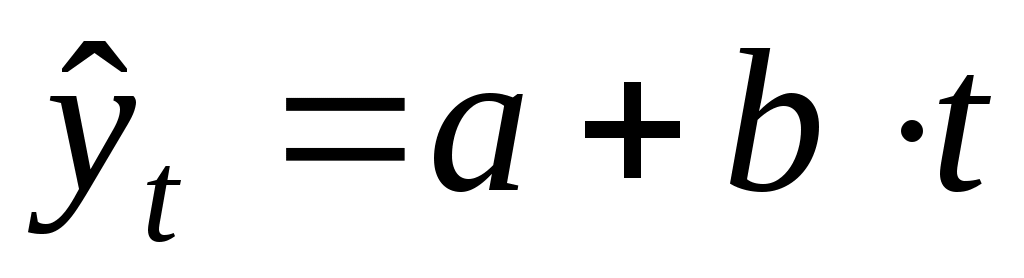
  
• 
  степенная: ;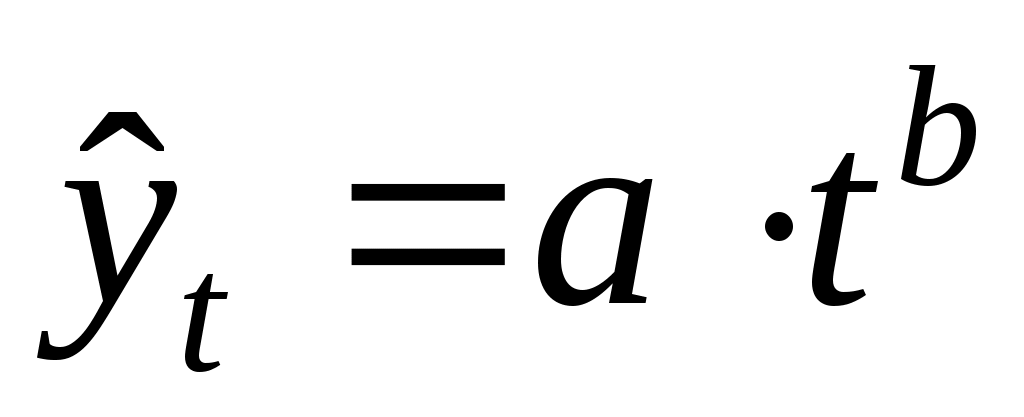
  
• 
  гиперболическая: ;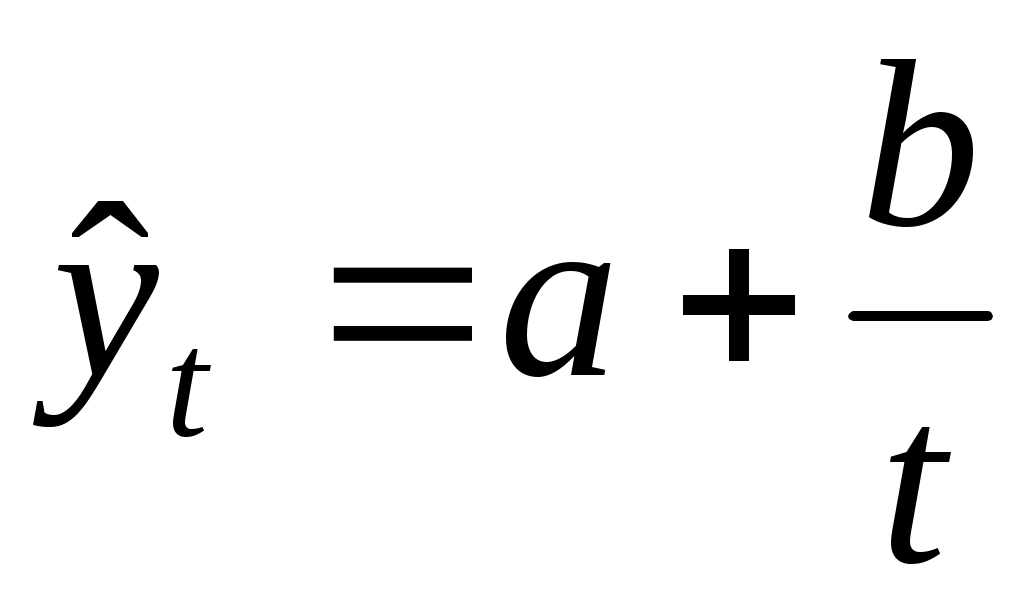
  
• 
  экспоненциальная: ;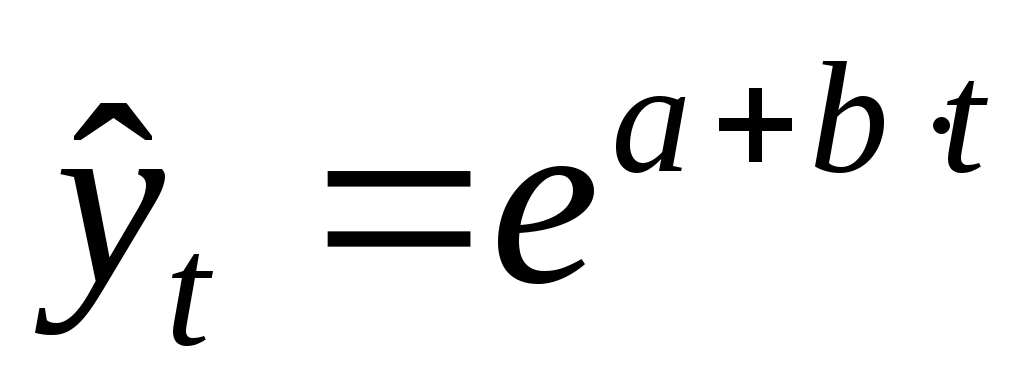
  
• 
  полиномы второго и более высоких порядков: .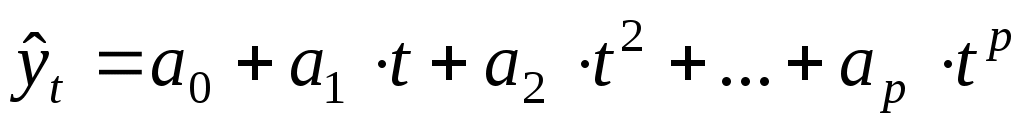
  

Расчет параметров тренда производится методом МНК. В качестве зависимой переменной выступают фактические уровни ряда , а независимой переменной является время . Заметим, что для нелинейных трендов необходима процедура линеаризации, аналогичная рассмотренной в разделе 3.

Выбор функции тренда может быть осуществлен несколькими способами. Наиболее простым считается тот, в ходе которого анализируют цепные абсолютные приросты (первые разности уровней ряда) , абсолютные ускорения уровней ряда (вторые разности ряда) и цепные коэффициенты роста .

Если примерно одинаковы , то ряд имеет линейный тренд, если же примерно постоянны , то для описания тенденции временного ряда следует выбрать параболу второго порядка, и, если примерно равны , необходимо использовать экспоненциальную или степенную функции.

Пример 1.⁹ Рассчитаем параметры уравнения тренда по следующим данным:

Таблица 5.2

Темпы роста номинальной месячной заработной платы (за 10 месяцев 1999г., % к уровню декабря 1998г.)

Месяц	Темп роста номинальной заработной платы	Месяц	Темп роста номинальной заработной платы
Январь	82,9	Июнь	121,6
Февраль	87,3	Июль	118,6
Март	99,4	Август	114,1
Апрель	104,8	Сентябрь	123,0
Май	107,2	Октябрь	127,3

---