 163  2(20) = 8; клетка на пересечении второй строки и третьего столбца:

«3»	2
4	3

33  42 = 1;

клетка на пересечении третьей строки и третьего столбца:

«3»	2
	
4	5

53  42 = 7;

клетка на пересечении четвертой строки и третьего столбца:

«3»	2
	
- 20	- 18

 183  (20)2 = 14;

клетка на пересечении второй строки и четвертого столбца:

«3»		20
4		40

403  420 = 40;

клетка на пересечении третьей строки и четвертого столбца:

«3»		20
		
4		24

243  420 = 8;

клетка на пересечении четвертой строки и четвертого столбца:

«3»		20
		
- 20		0

03  (20) 20= 400.

Таким образом, получаем следующую таблицу:

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	2 2	«3» 1	2 2	20 20
y2	x5	6 10	4 -4	3 1	40 40
y3	x6	2 -2	4 -4	5 7	24 -8
cj		- 16 -8	- 20 20	- 18 -14	0 400

---

7. Построение новой симплекс-таблицы.

Правила построения новой симплекс-таблицы

Изменяют базисные переменные: меняют местами переменные из разрешающей строки и разрешающего столбца. Элементы из нижних клеток предыдущей симплекс-таблицы делят на верхний разрешающий элемент и записывают на соответствующие места в верхние клетки новой симплекс-таблицы.

Если в новой таблице в строке есть отрицательные элементы, то следует сделать следующий шаг симплекс-метода. (Нецелесообразно выбирать за разрешающую строку – те же строки, что и на предыдущих шагах).

Если в новой таблице в строке нет отрицательных элементов, а в столбце свободных членов остались отрицательные элементы, то строка с отрицательным значением 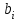выбирается за разрешающую, и выполняется следующий шаг симплекс-метода.

Если в строке есть нулевой элемент, то это признак альтернативного оптимума для ПЗЛП. Для нахождения альтернативного решения выполняется еще один шаг симплекс-метода: Столбец с нулевым элементом в строке выбирается за разрешающий. Находят неотрицательные отношения столбца свободных членов к соответствующим элементам разрешающего столбца. Из полученных отношений выбирают минимальное неотрицательное отношение – это разрешающая строка, разрешающий элемент найден. Затем выполняют еще один шаг симплекс-метода.

Если в столбце 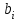есть нулевой элемент, то это признак альтернативного оптимума для ДЗЛП. Для нахождения альтернативного решения выполняется еще один шаг симплекс-метода. При этом строка с нулевым элементом в столбце 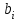выбирается за разрешающую.

Переходим к следующей симплекс-таблице. При этом в первую строку включается пара переменных х₂

---

, у₅, соответствующих разрешающему столбцу, а во второй столбец вводится пара переменных х₄, у₁, соответствующая разрешающей строке. Верхние части клеток заполняются элементами, полученными в результате деления соответствующих (стоящих на аналогичном месте) элементов из предыдущей таблицы в нижних частях клеток на разрешающий элемент «3»:

	yбаз	y4	y1	y6
yсв	xсв xбаз	- x1	- x4	- x3	bi
y5	x2	2/3	1/3	2/3	20/3
y2	x5	10/3	-4/3	1/3	40/3
y3	x6	-2/3	-4/3	7/3	-8/3
cj		-8/3	20/3	-14/3	400/3

Решение ПЗЛП на втором шаге двойственного симплекс-метода также выписывается по строкам: = (0, 20/3, 0, 0, 40/3, 8/3), = 400/3, решение ДЗЛП выписывается по столбцам: 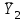= (20/3, 0, 0, 8/3, 0, 14/3), 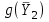= 400/3. Данное решение также не оптимальное, поскольку в строке

---

еще остались отрицательные элементы. Необходимо продолжить поиск оптимального решения.

В строке выбираем отрицательный элемент «8/3». Над ним выбираем положительный, предпочтительнее «10/3», поскольку первая строка была выбрана на предыдущем шаге метода, следовательно, вторая строка – разрешающая (выделена жирным шрифтом):

	yбаз	y4	y1	y6
yсв	xсв xбаз	- x1	- x4	- x3	bi
y5	x2	2/3	1/3	2/3	20/3
y2	x5	«10/3»	-4/3	1/3	40/3
y3	x6	-2/3	-4/3	7/3	-8/3
cj		-8/3	20/3	-14/3	400/3
					-

---

Находим максимальное отношение среди отношений элементов в строке целевой функции к соответствующим элементам разрешающей строки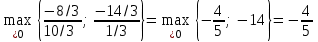

. Разрешающий столбец – первый, поскольку максимальное отношение соответствует ему.

Разрешающий элемент «10/3» находится на пересечении разрешающей строки и разрешающего столбца.

Заполнение нижних частей клеток осуществляется аналогично рассмотренному выше. Получаем следующую таблицу:

	yбаз	y4	y1	y6
yсв	xсв xбаз	- x1	- x4	- x3	bi
y5	x2	2/3 -2/3	1/3 2	2/3 2	20/3 40/3
y2	x5	«10/3» 1	-4/3 -4/3	1/3 1/3	40/3 40/3
y3	x6	-2/3 2/3	-4/3 -16/3	7/3 8	-8/3 0
cj		-8/3 8/3	20/3 56/3	-14/3 44/3	400/3 1440/3

Переходим к следующей симплекс-таблице. При этом во вторую строку включается пара переменных х₁, у₄, соответствующих разрешающему столбцу, а в первый столбец вводится пара переменных

---

Смотрите также файлы

• Повышение конкурентоспособности организации на рынке гигиенических продуктов (на примере ооо Эссити).pdf

• Практических заданий по дисциплине жанры мультимедиа.docx

• Задачи представленной работы, способствующие достижению цели.docx

• 1. Данные, определенным образом организованные, имеющие смысл, значение и ценность для своего потребителя и необходимые для принятия им решений, а также реализации других функций и действий, это .docx

• Частное профессиональное образовательное учреждение Гуманитарный колледж Эдельвейс задание.docx