Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 185
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х5 выводится из базисных переменных. На пересечении разрешающих строки и столбца находится разрешающий элемент «4»:
Переходим к третьему шагу симплекс-метода.
Заполним симплекс-таблицу третьего шага для варианта 0. Вместо переменной х5 вводим в базис переменную х1, в целевой функции ей соответствует коэффициент 16, который вносится в соответствующую клетку столбца сi. Аналогично предыдущему шагу заполняем ключевую строку, столбцы базисных переменных и остальные клетки:
Поскольку все оценки положительные j, то полученное опорное решение является оптимальным: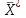 = (4, 4, 0, 0, 0, 0), а максимальное значение целевой функции равно
= (4, 4, 0, 0, 0, 0), а максимальное значение целевой функции равно 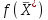 = 144.
= 144.
Учитывая соответствие переменных взаимно двойственных задач, можно выписать оптимальное решение двойственной задачи. Значения соответствующих переменных берут из последней строки последней симплекс-таблицы:
Таким образом,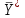
= (0, 3/2, 7/2, 0, 0, 4), поскольку y1x4, y2x5, y3x6, y4x1, y5x2, y6x3. Значение целевой функции = 144.
= 144.
Экономический смысл всех переменных, участвующих в решении
Экономический смысл переменных, участвующих в решении отражен в таблице
Экономический смысл переменных:
x1*, x2*, x3* -основные переменные - оптимальный план производства;
x4*, x5, x6* - дополнительные переменные - остатки ресурсов;
y1, y2, y3 -основные переменные - скрытые цены ресурсов;
y4, y5, y6 -дополнительные переменны – превышение затрат на ресурсы над ценой реализации (возможный убыток от производства продукции).
Наличие пары нулевых переменных x4* = 0 и y1 = 0 свидетельствует, что двойственная задача имеет альтернативные решения.
Анализ решения ПЗЛП
Подставим оптимальные значения переменных x* в исходную систему ограничений ПЗЛП:
1) 2х1 + 3х2 + 2х3 20
24 + 34 + 20 = 20
20 = 20, следовательно, х4 = 0, ресурс Р1 используется полностью;
2) 6х1 + 4х2 + 3х3 40
64 + 44 + 30 = 40
40 = 40, следовательно, х5 = 0, ресурс Р2 используется полностью;
3) 2х1 + 4х2 + 5х3 24
24 + 44 + 50 = 24
24 = 24, следовательно, х6 = 0, ресурс Р3 используется полностью.
Анализ решения ДЗЛП
Подставим оптимальные значения переменных у* в исходную систему ограничений ПЗЛП:
1) 2у1 + 6у2 + 2у3 16
20 + 6(3/2) + 2(7/2) = 16
16 = 16, следовательно, у4 = 0, убытки от производства первого вида продукции П1, которая вошла в оптимальный план производства отсутствуют;
2) 3у1 + 4у2 + 4у3 20
30 + 4(3/2) + 4(7/2) = 20
20 = 20, следовательно, у5 = 0, убытки от производства второго вида продукции П2, которая вошла в оптимальный план производства отсутствуют;
3) 2у1 + 3у2 + 5у3 18
20 + 3(3/2) + 5(7/2) = 22
22 18 на 4, следовательно, у6 = 4, убытки от производства третьего вида продукции П3, которая не вошла в оптимальный план производства, в случае ее производства будут составлять 4 ден. ед. с каждого изделия третьего вида.
4. Расчет границ изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана
Ресурсы, которые используются полностью, называются дефицитными. Признаком дефицитности ресурсов является отличие от нуля соответствующей данному ресурсу двойственной переменной и равенство нулю соответствующей дополнительной переменной.
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 |  | min |
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | bi/ hij | |
| 0 | x4 | 1/2 | 0 | -7/4 | 1 | 0 | -3/4 | 2 | 2/(1/2) |
| 0 | x5 | «4» | 0 | -2 | 0 | 1 | -1 | 16 | 16/4 |
| 20 | х2 | 1/2 | 1 | 5/4 | 0 | 0 | 1/4 | 6 | 6/(1/2) |
| j | -6 | 0 | 7 | 0 | 0 | 5 | 120 | - | |
Переходим к третьему шагу симплекс-метода.
Заполним симплекс-таблицу третьего шага для варианта 0. Вместо переменной х5 вводим в базис переменную х1, в целевой функции ей соответствует коэффициент 16, который вносится в соответствующую клетку столбца сi. Аналогично предыдущему шагу заполняем ключевую строку, столбцы базисных переменных и остальные клетки:
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 |  | min | ||||||||
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | bi/ hij | |||||||||
| 0 | x4 | 0 | 0 | -3/2 | 1 | -1/8 | -5/8 | 0 | | ||||||||
| 16 | x1 | 1 | 0 | -1/2 | 0 | 1/4 | -1/4 | 4 | | ||||||||
| 20 | х2 | 0 | 1 | 3/2 | 0 | -1/8 | 3/8 | 4 | | ||||||||
| j | 0 | 0 | 4 | 0 | 3/2 | 7/2 | 144 | - | |||||||||
Поскольку все оценки положительные j, то полученное опорное решение является оптимальным:
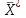 = (4, 4, 0, 0, 0, 0), а максимальное значение целевой функции равно
= (4, 4, 0, 0, 0, 0), а максимальное значение целевой функции равно 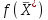 = 144.
= 144.Учитывая соответствие переменных взаимно двойственных задач, можно выписать оптимальное решение двойственной задачи. Значения соответствующих переменных берут из последней строки последней симплекс-таблицы:
| сi | сj | 16 | 20 | 18 | 0 | 0 | 0 |  |
| Базисные переменные (БП) | х1 | х2 | х3 | х4 | х5 | х6 | bi | |
| 0 | x4 | 0 | 0 | -3/2 | 1 | -1/8 | -5/8 | 0 |
| 16 | x1 | 1 | 0 | -1/2 | 0 | 1/4 | -1/4 | 4 |
| 20 | х2 | 0 | 1 | 3/2 | 0 | -1/8 | 3/8 | 4 |
| j | 0 | 0 | 4 | 0 | 3/2 | 7/2 | 144 | |
| yi | y4 | y5 | y6 | y1 | y2 | y3 | 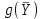 | |
Таким образом,
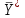
= (0, 3/2, 7/2, 0, 0, 4), поскольку y1x4, y2x5, y3x6, y4x1, y5x2, y6x3. Значение целевой функции
 = 144.
= 144.Экономический смысл всех переменных, участвующих в решении
Экономический смысл переменных, участвующих в решении отражен в таблице
| Компоненты оптимального решения ПЗЛП | |||||
| План производства | Остатки ресурсов, единиц | ||||
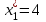  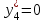 | 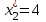  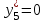 | 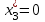  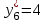 | 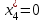  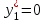 | 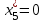  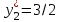 | 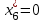  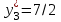 |
| Превышение затрат на ресурсы над ценой реализации (возможный убыток от производства продукции) | Объективно обусловленные оценки ресурсов (теневые, условные, скрытые цены ресурсов) | ||||
| Компоненты оптимального решения ДЗЛП | |||||
Экономический смысл переменных:
x1*, x2*, x3* -основные переменные - оптимальный план производства;
x4*, x5, x6* - дополнительные переменные - остатки ресурсов;
y1, y2, y3 -основные переменные - скрытые цены ресурсов;
y4, y5, y6 -дополнительные переменны – превышение затрат на ресурсы над ценой реализации (возможный убыток от производства продукции).
Наличие пары нулевых переменных x4* = 0 и y1 = 0 свидетельствует, что двойственная задача имеет альтернативные решения.
Анализ решения ПЗЛП
Подставим оптимальные значения переменных x* в исходную систему ограничений ПЗЛП:
1) 2х1 + 3х2 + 2х3 20
24 + 34 + 20 = 20
20 = 20, следовательно, х4 = 0, ресурс Р1 используется полностью;
2) 6х1 + 4х2 + 3х3 40
64 + 44 + 30 = 40
40 = 40, следовательно, х5 = 0, ресурс Р2 используется полностью;
3) 2х1 + 4х2 + 5х3 24
24 + 44 + 50 = 24
24 = 24, следовательно, х6 = 0, ресурс Р3 используется полностью.
Анализ решения ДЗЛП
Подставим оптимальные значения переменных у* в исходную систему ограничений ПЗЛП:
1) 2у1 + 6у2 + 2у3 16
20 + 6(3/2) + 2(7/2) = 16
16 = 16, следовательно, у4 = 0, убытки от производства первого вида продукции П1, которая вошла в оптимальный план производства отсутствуют;
2) 3у1 + 4у2 + 4у3 20
30 + 4(3/2) + 4(7/2) = 20
20 = 20, следовательно, у5 = 0, убытки от производства второго вида продукции П2, которая вошла в оптимальный план производства отсутствуют;
3) 2у1 + 3у2 + 5у3 18
20 + 3(3/2) + 5(7/2) = 22
22 18 на 4, следовательно, у6 = 4, убытки от производства третьего вида продукции П3, которая не вошла в оптимальный план производства, в случае ее производства будут составлять 4 ден. ед. с каждого изделия третьего вида.
4. Расчет границ изменения дефицитных ресурсов, в пределах которых не изменится структура оптимального плана
Ресурсы, которые используются полностью, называются дефицитными. Признаком дефицитности ресурсов является отличие от нуля соответствующей данному ресурсу двойственной переменной и равенство нулю соответствующей дополнительной переменной.