Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 492

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕУчебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.Пособие состоит из четырех разделов: Введение в теорию вероятностей. Основные понятия и термины статистики. Статистические методы обработки экспериментальных данных. Компьютерная обработка данных анализа в специализированной программе EasyStatistics. Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей. Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами. Каждый раздел содержит список вопросов и заданий для самопроверки.Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙЗакономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.Понятие о случайном событииОпыт, эксперимент, на­блюдение явления называются испытанием. Испытаниями, напри­мер, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).Результат, исход испытания называется событием. Для обозначения событий используются большие буквы ла­тинского алфавита: А, В, С и т. д.Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появле­ние четного числа очков. События Аи В совместимые.Два события называются несовместимы­ми, если появление одного из них исключает появление другого в одном и том же испытании.Испытание: однократное бросание монеты. Собы­тие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.Несовместимость более чем двух событий означает их попарную несовместимостьИспытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпа­дение одного очка, двух, трех и т. д. Эти события являются несов­местимыми..Два события А и В называются проти­воположными, если в данном испытании они несовместимы и одно из них обязательно происходит.Событие, противоположное событию А, обозначают через А.Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В или А = В.Событие называется достоверным, если в данном испытании оно является единственно возможным его ис­ходом, и невозможным, если в данном испытании оно заведомо не может произойти.Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.Достоверное и невозможное события в данном испытании являются противоположными.Событие А называется случайным, если оно объективно может наступить или не наступить в данном испы­тании.Выпадение шести очков при броса­нии игральной кости — случайное событие. Оно может наступить, но может и не наступить в данном испытании.Прорастание девяноста восьми зерен пшеницы из ста — случайное событие. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.Классическое определение вероятностиВсякое испыта­ние влечет за собой некоторую совокупность исходов — резуль­татов испытания, т. е. событий. Во многих случаях возможно пере­числить все события, которые могут быть исходами данного испы­тания.Говорят, что совокупность событий обра­зует полную группу событий для данного испытания, если его ре­зультатом обязательно становится хотя бы одно из них.События Ul, U2, ..., Un , образующие полную группу попарно несовместимых и равновозможных собы­тий, будем называть элементарными событиями.Вернемся к опыту с подбрасыванием игральной кости. Пусть Ui — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U1, U2, …, U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметрич­ной, то события U1, U2, …, U6 являются и равновозможными, т. е. элементарными.Событие А называется благоприят­ствующим событию В, если наступление события А влечет за собой наступление события В.Пусть при бросании игральной кости события U2, U4 и U6 — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного очка; собы­тия U2, U4 и U6 благоприятствуют событию А.Классическое определение вероятностиВероятностью Р (А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба и событие В — выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно со­бытие — само А, т. е. здесь m = 1. Поэтому Р(А) = 0,5.Найти вероятность того, что при бросании иг­ральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятст­вующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому .Из приведенного классического определения вероятности вы­текают следующие ее свойства.1. Вероятность достоверного события равна единице.Действительно, достоверному событию должны благоприят­ствовать все n элементарных событий, т. е. m = n и, следовательно, P(A)=1.2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприят­ствовать ни одно из элементарных событий, т. е. m = 0, откуда P(A)=0.3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n , значит, 0 <= Р (А)<= 1.Относительная частота.Статистическое определение ве­роятности.Классическое определение вероятности не являет­ся пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.В таких случаях используется так называемое статистическое определение вероятности.Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной часто­той (или просто частотой) события А, а отношение называется относительной частотой события А.При транспортировке из 10 000 арбузов испор­тилось 26. Здесь m= 26 — абсолютная частота испорченных ар­бузов, а P*(A)=0,0026 относительная.Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(A) принимает зна­чения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относитель­ная частота Р*(А) приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500;0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5Статистическое определение вероят­ностиВероятностью события А в данном испытании называется число Р (А), около которого группируются значения относительной частоты при больших n.По официальным данным шведской статистики, относительные частоты рождения девочек по месяцам 2007 г. харак­теризуются следующими числами (расположены в порядке сле­дования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты группируются около числа 0,482.Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Геометрическая вероятностьДо этого мы рассматривали возможные эксперименты, в которых реализуется конечное множество событий. Однако существует большое количество задач, для которых такое предположение не является справедливым. При решении таких задач предполагается, что множество реализуемых событий может быть представлено в виде некоторой геометрической фигуры, а конкретное событие соответствует точке заданной части этой фигуры. В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме больше P(Ω) = 1.Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.Мишень имеет форму окружности. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены. Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем P=0,5Студент и студентка договариваются о встрече на заданном промежутке времени Т. Тот, кто приходит первым ожидает другого в течение времени tВ качестве множества элементарных событий рассмотри квадрат, состоящий из точек (x,y), 0<=x<=T, 0<=y<=T, где x и у время прихода его и ее.Благоприятсвующие события образуют точки, для которых |x-y|<t, т.е. точки квадрата между прямыми y=x-t, y=x+t. Площадь получающейся фигуры равна T2-(T-t)2, а площадь всего квадрата – Т2. Отсуда искомая вероятность Свойства вероятностейСложение вероятностей несовместимых событийСуммой событий А и В называется собы­тие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.Стрельба двух стрелков (каждый де­лает по одному выстрелу). Событие А — попадание в мишень пер­вым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень по крайней мере одним стрелком.Произведением событий А и В назы­вается событие С = АВ, состоящее в том, что в результате испыта­ния произошло и событие А, и событие В.Аналогично произведением конечного числа событий A1 А2, …, Ak называется событие А = А1 * A2 * ... * Ak, состоящее в том, что в результате испытания произошли все указанные события.В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.Из определения непосредственно следует, что АВ = ВА.Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:Р (А + В) = Р (А) + Р (В). Следствие. Сумма вероятностей противоположных собы­тий А и А равна единице:Р(А) + Р(А

Коэффициент сопряженности Чупрова. Дальнейшим обоб-щением четырехпольных таблиц являются многопольные таблицы, для которых сопряженность наиболее часто оценивается по формуле, предложенной русским статистиком А. А. Чупровым. Прежде чем приводить ее рассмотрим несколько реальных ситуаций, когда такая оценка может потребоваться. Известно, например, что окраска тюльпанов связана с наличием определенных пигментов. Может представлять интерес вопрос о том, с какими именно пигментами преимущественно связана та или иная окраска цветка. Или другой пример. Окружающая гнездо полярной крачки обстановка может представлять собой зеленые растения, растения и гальку, пестрые камешки и т. д. При этом можно наблюдать самые разные по качеству гнезда: от его отсутствия до очень хорошо сделанного. В этом случае желательно знать, связано ли качество гнезда с какой-то одной или несколькими характеристиками окружающей среды. Общим для этих и других подобных задач является то, что в распоряжении экспериментатора оказываются данные о некотором множестве объектов, обладающих двумя признаками, причем каждый из признаков может иметь несколько градаций. В этом случае , где m - число разновидностей явления Х; k - число разновидностей явления Y, n – общее число объектов (m*k). Независимо то того, что каждый из описательных признаков, несмотря на разницу в численности его разновидностей, можно свести к альтернативному - только с двумя разновидностями, довольно часто в практике возникает необходимость работать с описательными признаками более двух разновидностей. В таких случаях необходимо при вычислении коэффициента корреляции составлять так называемую корреляционную таблицу (где X1,X2,...Xn - обозначают разновидность одного признака, а Y1, Y2... Yn - разновидности другого).При наличии такой схемы коэффициент корреляции находят по формуле: , где - коэффициент связи, m- число разновидностей явления Х; k - число разновидностей явления Y.Данный метод пригоден также и для экспрессной оценки связи между количественными (например возраст) и качествен-ными (например брак) параметрами.На практике (особенно в зоологии и ботанике) довольно часто встречаются другие меры измерения связи.



 Теоретически, мы ожидаем, что частоты распределятся равновероятно, т.е.  частота распределится пропорционально между мальчиками и девочками. Построим таблицу теоретических частот. Для этого умножим сумму по строке на сумму по столбцу и разделим получившееся число на общую суму (n).

 

 
«Активный»
«Старательный»
«Дисциплинированный»
Итого:

Мальчики
(21 * 16)/48 = 7
(21 * 17)/48 = 7.44
(21 * 15)/48 = 6.56
21

Девочки
(27 * 16)/48 = 9
(27 * 17)/48 = 9.56
(27 * 15)/48 = 8.44
27

Итого:
16
17
15
n = 48

 

Итоговая таблица для вычислений будет выглядеть так:

Категория 1
Категория 2
Эмпирич.
Теоретич.
(Э-Т)2/Т

Мальчики
«Активный»
10
7
1,28

 
«Старательный»
5
7,44
0,8

 
«Дисциплини-рованный»
6
6,56
0,47

Девочки
«Активный»
6
9
1

 
«Старательный»
12
9,56
0,62

 
«Дисциплини-рованный»
9
8,44
0,04

 
 
 
 
Сумма: 4,21

 

В нашем случае хи-квадрат = 4,21; df= 2.

По таблице критических значений критерия находим: при df= 2 и уровне ошибки 0,05 критическое значение χ2  =  5,99.

Полученное значение меньше критического, а значит принимается нулевая гипотеза. Вывод: учителя не придают значение полу ребенка при написании ему характеристики.
Сравнение долей

Для сравнения частот применяется Т-критерий Стьюдента для долей



Точный тест Фишера
Точный метод Фишера—Ирвина (критерий Фишера—Ирвина, точный метод Фишера) применяется для проверки нулевой гипотезы о том, отобраны ли две исследуемые бинарные (дихотомические) выборки из генеральных совокупностей с одинаковой частотой встречаемости изучаемого эффекта. Рассматриваемый метод предназначен для обработки так называемых четырехпольных (четырехклеточных) таблиц, или таблиц «2 х 2».

Таблицы 2х2 или четырехпольные таблицы имеют вид

 
Есть эффект
Нет эффекта
 

1 группа
a
b
a+b

2 группа
c
d
c+d

 
a+c
b+d
a+b+c+d

где a,b,c,d - наблюдаемые частоты

a+b, c+d - суммы частот по строкам

a+c, b+d - суммы частот по колонкам

a+b+c+d - общее число наблюдений
В результате вычислений получается точное значение уровня значимости нулевой гипотезы. Вычисление производится по формуле:


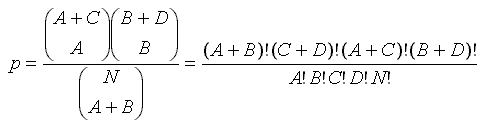
Допустим имеется таблица "2х2" следующего вида:

2
3

6
4

Подсчитываем маргинальные частоты для данной таблицы:

2
3
5

6
4
10

8
7
15

p=(2+3)!*(6+4)!*(2+6)!*(3+4)!/((2+3+6+4)!*2!*3!*6!*4!)=0,326

Для вычисления одностороннего значения уровня значимости необходимо найти сумму всех вероятностей для комбинаций данной таблицы со значениями от 0 до вероятности данной таблицы (0,326).


Для вычисления двустороннего значения уровня значимости необходимо найти сумму всех вероятностей для комбинаций данной таблицы со значениями меньше или равными данной таблицы (0,326).

Минимальная маргинальная частота равна 5, поэтому для данной таблицы возможно (5+1) комбинаций с заданными маргинальными частотами.


0
5
p=(0+5)!*(8+2)!*(0+8)!*(5+2)!/((0+8+5+2)!*0!*8!*5!*2!)=0,007

8
2










1
4
p=(1+4)!*(7+7)!*(1+7)!*(4+7)!/((1+4+7+7)!*1!*4!*7!*7!)=0,093

7
7










2
3
p=(2+3)!*(6+4)!*(2+6)!*(3+4)!/((2+3+6+4)!*2!*3!*6!*4!)=0,326

6
4










3
2
p=(3+2)!*(5+5)!*(3+5)!*(2+5)!/((3+2+5+5)!*3!*2!*5!*5!)=0,392

5
5










4
1
p=(4+1)!*(4+6)!*(4+4)!*(1+6)!/((4+1+4+6)!*4!*1!*4!*6!)=0,163

4
6










5
0
p=(5+0)!*(3+7)!*(5+3)!*(0+7)!/((5+0+3+7)!*5!*0!*3!*7!)=0,019

3
7


Таким образом уровень значимости для односторонней гипотезы составляет:

P=0,326 +0,093 + 0,007 = 0,426
а для двусторонней гипотезы:
P=0,326 + 0,093 + 0,007 + 0,163 + 0,019 = 0,608

Сравнение более двух независимых групп

Однофакторный дисперсионный анализ Фишера
Дисперсионный анализ — это статистический метод оценки связи между факторными и результативным признаками в различных группах, отобранный случайным образом, основанный на определении различий (разнообразия) значений признаков. В основе дисперсионного анализа лежит анализ отклонений всех единиц исследуемой совокупности от среднего арифметического. В качестве меры отклонений берется дисперсия (В)— средний квадрат отклонений. Отклонения, вызываемые воздействием факторного признака (фактора) сравниваются с величиной отклонений, вызываемых случайными обстоятельствами. Если отклонения, вызываемые факторным признаком, более существенны, чем случайные отклонения, то считается, что фактор оказывает существенное влияние на результативный признак.

Для того, чтобы вычислить дисперсию значения отклонений каждой варианты (каждого зарегистрированного числового значения признака) от среднего арифметического возводят в квадрат. Тем самым избавляются от отрицательных знаков. Затем эти отклонения (разности) суммируют и делят на число наблюдений, т.е. усредняют отклонения. Таким образом, получают значения дисперсий.

Важным методическим значением для применения дисперсионного анализа является правильное формирование выборки. В зависимости от поставленной цели и задач выборочные группы могут формироваться случайным образом независимо друг от друга (контрольная и экспериментальная группы для изучения некоторого показателя, например, влияние высокого артериального давления на развитие инсульта). Такие выборки называются независимыми.

Нередко результаты воздействия факторов исследуются у одной и той же выборочной группы (например, у одних и тех же пациентов) до и после воздействия (лечение, профилактика, реабилитационные мероприятия), такие выборки называются зависимыми.

Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным (одномерный анализ). При изучении влияния более чем одного фактора используют многофакторный дисперсионный анализ (многомерный анализ).


Факторные признаки — это те признаки, которые влияют на изучаемое явление.

Результативные признаки — это те признаки, которые изменяются под влиянием факторных признаков.

Условия применения дисперсионного анализа:

Задачей исследования является определение силы влияния одного (до 3) факторов на результат или определение силы совместного влияния различных факторов (пол и возраст, физическая активность и питание и т.д.).

Изучаемые факторы должны быть независимые (несвязанные) между собой. Например, нельзя изучать совместное влияние стажа работы и возраста, роста и веса детей и т.д. на заболеваемость населения.

Подбор групп для исследования проводится рандомизированно (случайный отбор). Организация дисперсионного комплекса с выполнением принципа случайности отбора вариантов называется рандомизацией (перев. с англ. — random), т.е. выбранные наугад.

Можно применять как количественные, так и качественные (атрибутивные) признаки.

При проведении однофакторного дисперсионного анализа рекомендуется (необходимое условие применения):

  1. Нормальность распределения анализируемых групп или соответствие выборочных групп генеральным совокупностям с нормальным распределением.

  2. Независимость (не связанность) распределения наблюдений в группах.

  3. Наличие частоты (повторность) наблюдений.

Сначала формулируется нулевая гипотеза, то есть предполагается, что исследуемые факторы не оказывают никакого влияния на значения результативного признака и полученные различия случайны.

Затем определяем, какова вероятность получить наблюдаемые (или более сильные) различия при условии справедливости нулевой гипотезы.

Если эта вероятность мала, то мы отвергаем нулевую гипотезу и заключаем, что результаты исследования статистически значимы. Это еще не означает, что доказано действие именно изучаемых факторов (это вопрос, прежде всего, планирования исследования), но все же маловероятно, что результат обусловлен случайностью.

При выполнении всех условий применения дисперсионного анализа, разложение общей дисперсии математически выглядит следующим образом:

Doбщ. = Dфакт + D ост.,

Doбщ. - общая дисперсия наблюдаемых значений (вариант), характеризуется разбросом вариант от общего среднего. Измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Общее разнообразие складывается из межгруппового и внутригруппового;

Смотрите также файлы