Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 491

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕУчебно-методическое пособие знакомит студентов с основными понятиями о теории вероятностей, случайных процессах, статистическом оценивании и проверке гипотез, статистических методах обработки экспериментальных данных, математических методах, принятых в биологических исследованиях.Пособие состоит из четырех разделов: Введение в теорию вероятностей. Основные понятия и термины статистики. Статистические методы обработки экспериментальных данных. Компьютерная обработка данных анализа в специализированной программе EasyStatistics. Введение в теорию вероятностей дает представление о случайных событиях, вероятности и ее свойствах, случайных величинах и основных теоретических распределениях случайных величин.При изучении второго раздела разбираются понятия о совокупности и выборке, классификации признаков, дается представление о схемах научного эксперимента и научных гипотезах, достоверности и надежности результатов.Третий раздел знакомит со статистическими методами описания групп, способами их сравнения в зависимости от характера распределения исходных данных. Большое внимание уделено корреляционно-регрессионному анализу, лежащему в основе многомерных методов анализа. Разбираются широко распространенные в биологических исследованиях методы оценки динамики, цикличности и классификации. При описании каждого метода описываются условия, необходимые для проведения статистической обработки, и возможные трудности в интерпретации полученных показателей. Четвертый раздел посвящен практическому применению методов статистической обработки данных с помощью специализированной программы «Статистическая обработка медико-биологических данных» (EasyStatistics). Данная программа разработана автором пособия (Роспатент №2003612171) и предназначена для статистической обработки данных биологических и медицинских исследований и, в первую очередь, нацелена на выполнение курсовых и дипломных работ студентами. В то же время это не замена уже существующим мощным статистическим пакетам, таким как Statistica, а скорее дополнение, помогающее оценить возможности манипулирования данными и принципы работы с основными статистическими методами. Каждый раздел содержит список вопросов и заданий для самопроверки.Пособие также содержит список учебно-методических материалов, рекомендуемых для самостоятельной работы студентов.РАЗДЕЛ I. ВВЕДЕНИЕ В ТЕОРИЮ ВЕРОЯТНОСТЕЙЗакономерности, которым подчиняются случайные события, изучаются в разделах математики, которые называются теорией вероятностей и математической статистикой.Понятие о случайном событииОпыт, эксперимент, на­блюдение явления называются испытанием. Испытаниями, напри­мер, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).Результат, исход испытания называется событием. Для обозначения событий используются большие буквы ла­тинского алфавита: А, В, С и т. д.Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.Испытание: однократное бросание игральной кости. Событие А — появление четырех очков. Событие В— появле­ние четного числа очков. События Аи В совместимые.Два события называются несовместимы­ми, если появление одного из них исключает появление другого в одном и том же испытании.Испытание: однократное бросание монеты. Собы­тие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.Несовместимость более чем двух событий означает их попарную несовместимостьИспытание: однократное бросание игральной кости. Пусть события А1, А2, А3, А4, А5, А6 соответственно выпа­дение одного очка, двух, трех и т. д. Эти события являются несов­местимыми..Два события А и В называются проти­воположными, если в данном испытании они несовместимы и одно из них обязательно происходит.Событие, противоположное событию А, обозначают через А.Испытание: бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т. е. А = В или А = В.Событие называется достоверным, если в данном испытании оно является единственно возможным его ис­ходом, и невозможным, если в данном испытании оно заведомо не может произойти.Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.Достоверное и невозможное события в данном испытании являются противоположными.Событие А называется случайным, если оно объективно может наступить или не наступить в данном испы­тании.Выпадение шести очков при броса­нии игральной кости — случайное событие. Оно может наступить, но может и не наступить в данном испытании.Прорастание девяноста восьми зерен пшеницы из ста — случайное событие. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.Классическое определение вероятностиВсякое испыта­ние влечет за собой некоторую совокупность исходов — резуль­татов испытания, т. е. событий. Во многих случаях возможно пере­числить все события, которые могут быть исходами данного испы­тания.Говорят, что совокупность событий обра­зует полную группу событий для данного испытания, если его ре­зультатом обязательно становится хотя бы одно из них.События Ul, U2, ..., Un , образующие полную группу попарно несовместимых и равновозможных собы­тий, будем называть элементарными событиями.Вернемся к опыту с подбрасыванием игральной кости. Пусть Ui — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U1, U2, …, U6 образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметрич­ной, то события U1, U2, …, U6 являются и равновозможными, т. е. элементарными.Событие А называется благоприят­ствующим событию В, если наступление события А влечет за собой наступление события В.Пусть при бросании игральной кости события U2, U4 и U6 — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного очка; собы­тия U2, U4 и U6 благоприятствуют событию А.Классическое определение вероятностиВероятностью Р (А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба и событие В — выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно со­бытие — само А, т. е. здесь m = 1. Поэтому Р(А) = 0,5.Найти вероятность того, что при бросании иг­ральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятст­вующих элементарных событий 3 (выпадение 2, 4 и 6). Поэтому .Из приведенного классического определения вероятности вы­текают следующие ее свойства.1. Вероятность достоверного события равна единице.Действительно, достоверному событию должны благоприят­ствовать все n элементарных событий, т. е. m = n и, следовательно, P(A)=1.2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприят­ствовать ни одно из элементарных событий, т. е. m = 0, откуда P(A)=0.3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0 < m < n , значит, 0 <= Р (А)<= 1.Относительная частота.Статистическое определение ве­роятности.Классическое определение вероятности не являет­ся пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.В таких случаях используется так называемое статистическое определение вероятности.Пусть произведено n испытаний, при этом некоторое событие А наступило m раз. Число m называется абсолютной часто­той (или просто частотой) события А, а отношение называется относительной частотой события А.При транспортировке из 10 000 арбузов испор­тилось 26. Здесь m= 26 — абсолютная частота испорченных ар­бузов, а P*(A)=0,0026 относительная.Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(A) принимает зна­чения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относитель­ная частота Р*(А) приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.Было проведено 10 серий бросаний монеты, по 1000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500;0,497; 0,494; 0,484. Эти частоты группируются около числа 0,5Статистическое определение вероят­ностиВероятностью события А в данном испытании называется число Р (А), около которого группируются значения относительной частоты при больших n.По официальным данным шведской статистики, относительные частоты рождения девочек по месяцам 2007 г. харак­теризуются следующими числами (расположены в порядке сле­дования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473. Эти частоты группируются около числа 0,482.Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Геометрическая вероятностьДо этого мы рассматривали возможные эксперименты, в которых реализуется конечное множество событий. Однако существует большое количество задач, для которых такое предположение не является справедливым. При решении таких задач предполагается, что множество реализуемых событий может быть представлено в виде некоторой геометрической фигуры, а конкретное событие соответствует точке заданной части этой фигуры. В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме больше P(Ω) = 1.Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω.Мишень имеет форму окружности. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены. Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем P=0,5Студент и студентка договариваются о встрече на заданном промежутке времени Т. Тот, кто приходит первым ожидает другого в течение времени tВ качестве множества элементарных событий рассмотри квадрат, состоящий из точек (x,y), 0<=x<=T, 0<=y<=T, где x и у время прихода его и ее.Благоприятсвующие события образуют точки, для которых |x-y|<t, т.е. точки квадрата между прямыми y=x-t, y=x+t. Площадь получающейся фигуры равна T2-(T-t)2, а площадь всего квадрата – Т2. Отсуда искомая вероятность Свойства вероятностейСложение вероятностей несовместимых событийСуммой событий А и В называется собы­тие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.Стрельба двух стрелков (каждый де­лает по одному выстрелу). Событие А — попадание в мишень пер­вым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С = А + В, состоящее в попадании в мишень по крайней мере одним стрелком.Произведением событий А и В назы­вается событие С = АВ, состоящее в том, что в результате испыта­ния произошло и событие А, и событие В.Аналогично произведением конечного числа событий A1 А2, …, Ak называется событие А = А1 * A2 * ... * Ak, состоящее в том, что в результате испытания произошли все указанные события.В условиях предыдущего примера произведением событий А и В будет событие С = АВ, состоящее в попадании в мишень двух стрелков.Из определения непосредственно следует, что АВ = ВА.Вероятность суммы двух несовместимых событий А и В равна сумме вероятностей этих событий:Р (А + В) = Р (А) + Р (В). Следствие. Сумма вероятностей противоположных собы­тий А и А равна единице:Р(А) + Р(А

Коэффициент сопряженности Чупрова. Дальнейшим обоб-щением четырехпольных таблиц являются многопольные таблицы, для которых сопряженность наиболее часто оценивается по формуле, предложенной русским статистиком А. А. Чупровым. Прежде чем приводить ее рассмотрим несколько реальных ситуаций, когда такая оценка может потребоваться. Известно, например, что окраска тюльпанов связана с наличием определенных пигментов. Может представлять интерес вопрос о том, с какими именно пигментами преимущественно связана та или иная окраска цветка. Или другой пример. Окружающая гнездо полярной крачки обстановка может представлять собой зеленые растения, растения и гальку, пестрые камешки и т. д. При этом можно наблюдать самые разные по качеству гнезда: от его отсутствия до очень хорошо сделанного. В этом случае желательно знать, связано ли качество гнезда с какой-то одной или несколькими характеристиками окружающей среды. Общим для этих и других подобных задач является то, что в распоряжении экспериментатора оказываются данные о некотором множестве объектов, обладающих двумя признаками, причем каждый из признаков может иметь несколько градаций. В этом случае , где m - число разновидностей явления Х; k - число разновидностей явления Y, n – общее число объектов (m*k). Независимо то того, что каждый из описательных признаков, несмотря на разницу в численности его разновидностей, можно свести к альтернативному - только с двумя разновидностями, довольно часто в практике возникает необходимость работать с описательными признаками более двух разновидностей. В таких случаях необходимо при вычислении коэффициента корреляции составлять так называемую корреляционную таблицу (где X1,X2,...Xn - обозначают разновидность одного признака, а Y1, Y2... Yn - разновидности другого).При наличии такой схемы коэффициент корреляции находят по формуле: , где - коэффициент связи, m- число разновидностей явления Х; k - число разновидностей явления Y.Данный метод пригоден также и для экспрессной оценки связи между количественными (например возраст) и качествен-ными (например брак) параметрами.На практике (особенно в зоологии и ботанике) довольно часто встречаются другие меры измерения связи.



Dфакт - факторная (межгрупповая) дисперсия, характеризуется различием средних в каждой группе и зависит от влияния исследуемого фактора, по которому дифференцируется каждая группа. Например, в группах различных по этиологическому фактору клинического течения пневмонии средний уровень проведенного койко-дня неодинаков — наблюдается межгрупповое разнообразие.

D ост. - остаточная (внутригрупповая) дисперсия, которая характеризует рассеяние вариант внутри групп. Отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неуточненных факторов и не зависящую от признака — фактора, положенного в основание группировки. Вариация изучаемого признака зависит от силы влияния каких-то неучтенных случайных факторов, как от организованных (заданных исследователем), так и от случайных (неизвестных) факторов.

Поэтому общая вариация (дисперсия) слагается из вариации, вызванной организованными (заданными) факторами, называемыми факториальной вариацией и неорганизованными факторами, т.е. остаточной вариацией (случайной, неизвестной).

Для выборки объема n выборочная дисперсия вычисляется как сумма квадратов отклонений от выборочного среднего, деленная на n-1 (объем выборки минус единица). Таким образом, при фиксированном объеме выборки n дисперсия есть функция суммы квадратов (отклонений), обозначаемая, для краткости, SS (от английского Sum of Squares - Сумма квадратов). Далее слово выборочная мы часто опускаем, прекрасно понимая, что рассматривается выборочная дисперсия или оценка дисперсии. В основе дисперсионного анализа лежит разделение дисперсии на части или компоненты. Рассмотрим следующий набор данных:


 
Группа 1
Группа 2

Наблюдение 1
2
6

Наблюдение 2
3
7

Наблюдение 3
1
5

Среднее
2
6

Сумма квадратов (СК)
2
2

Общее среднее
4

Общая сумма квадратов
28


Средние двух групп существенно различны (2 и 6 соответственно). Сумма квадратов отклонений внутри каждой группы равна 2. Складывая их, получаем 4. Если теперь повторить эти вычисления без учета групповой принадлежности, то есть, если вычислить SS исходя из общего среднего этих двух выборок, то получим величину 28. Иными словами, дисперсия (сумма квадратов), основанная на внутригрупповой изменчивости, приводит к гораздо меньшим значениям, чем при вычислении на основе общей изменчивости (относительно общего среднего). Причина этого, очевидно, заключается в существенной разнице между средними значениями, и это различие между средними и объясняет существующее различие между суммами квадратов.


 
SS
ст.св.

MS
F
p

Эффект
24.0
1
24.0
24.0
.008

Ошибка
4.0
4
1.0
 
 

Как видно из таблицы, общая сумма квадратов SS = 28 разбита на компоненты: сумму квадратов, обусловленную внутригрупповой изменчивостью (2+2=4; см. вторую строку таблицы) и сумму квадратов, обусловленную различием средних значений между группами (28-(2+2)=24; см первую строку таблицы). Заметим, что MS в этой таблице есть средний квадрат, равный SS, деленная на число степеней свободы (ст.св).

В рассмотренном выше простом примере вы могли бы сразу вычислить t-критерий для независимых выборок. Полученные результаты, естественно, совпадут с результатами дисперсионного анализа.

Однако, ситуации, когда некоторое явление полностью описывается одной переменной, чрезвычайно редки. Например, если мы пытаемся научиться выращивать большие помидоры, следует рассматривать факторы, связанные с генетической структурой растений, типом почвы, освещенностью, температурой и т.д. Таким образом, при проведении типичного эксперимента приходится иметь дело с большим количеством факторов. Основная причина, по которой использование дисперсионного анализа предпочтительнее повторного сравнения двух выборок при разных уровнях факторов с помощью серий t-критерия, заключается в том, что дисперсионный анализ существенно более эффективен и, для малых выборок, более информативен.


Предположим, что в рассмотренном выше примере анализа двух выборок мы добавим еще один фактор, например, Пол. Пусть каждая группа теперь состоит из 3 мужчин и 3 женщин. План этого эксперимента можно представить в виде таблицы:

 
Экспериментальная группа 1
Экспериментальная группа 2

Мужчины
2
6

 
3
7

 
1
5

Среднее
2
6

Женщины
4
8

3
5
9

1
3
7

Среднее
4
8

До проведения вычислений можно заметить, что в этом примере общая дисперсия имеет, по крайней мере, три источника:

  1. случайная ошибка (внутригрупповая дисперсия),

  2. изменчивость, связанная с принадлежностью к экспериментальной группе

  3. изменчивость, обусловленная полом объектов наблюдения.


Отметим, что существует еще один возможный источник изменчивости - взаимодействие факторов, который мы обсудим позднее). Что произойдет, если мы не будем включать пол как фактор при проведении анализа и вычислим обычный t-критерий? Если мы будем вычислять суммы квадратов, игнорируя пол (т.е. объединяя объекты разного пола в одну группу при вычислении внутригрупповой дисперсии и получив при этом сумму квадратов для каждой группы равную SS =10 и общую сумму квадратов SS = 10+10 = 20), то получим большее значение внутригрупповая дисперсии, чем при более точном анализе с дополнительным разбиением на подгруппы по полу (при этом внутригрупповые средние будут равны 2, а общая внутригрупповая сумма квадратов равна SS = 2+2+2+2 = 8).

Итак, при введении дополнительного фактора: пол, остаточная дисперсия уменьшилась. Это связано с тем, что среднее значение для мужчин меньше, чем среднее значение для женщин, и это различие в средних значениях увеличивает суммарную внутригрупповую изменчивость, если фактор пола не учитывается. Управление дисперсией ошибки увеличивает чувствительность (мощность) критерия.


На этом примере видно еще одно преимущество дисперсионного анализа по сравнению с обычным t-критерием для двух выборок. Дисперсионный анализ позволяет изучать каждый фактор, управляя значениями других факторов. Это, в действительности, и является основной причиной его большей статистической мощности (для получения значимых результатов требуются меньшие объемы выборок). По этой причине дисперсионный анализ даже на небольших выборках дает статистически более значимые результаты, чем простой t-критерий.


Критерий Краскела-Уоллиса
Критерий Краскела-Уоллиса - это непараметрическая альтернатива одномерному (межгрупповому) дисперсионному анализу. Он используется для сравнения трех или более выборок, и проверяет нулевые гипотезы, согласно которым различные выборки были взяты из одного и того же распределения, или из распределений с одинаковыми медианами. Таким образом, интерпретация критерия Краскела-Уоллиса в основном сходна с параметрическим одномерным дисперсионным анализом, за исключением того, что этот критерий основан скорее на рангах, чем на средних.

Сравнение двух зависимых групп
Парный Т критерий Стьюдента
В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:



где di=xi-yi — разности между соответствующими значениями переменной X и переменной У, а d - среднее этих разностей;

Sd вычисляется по следующей формуле:



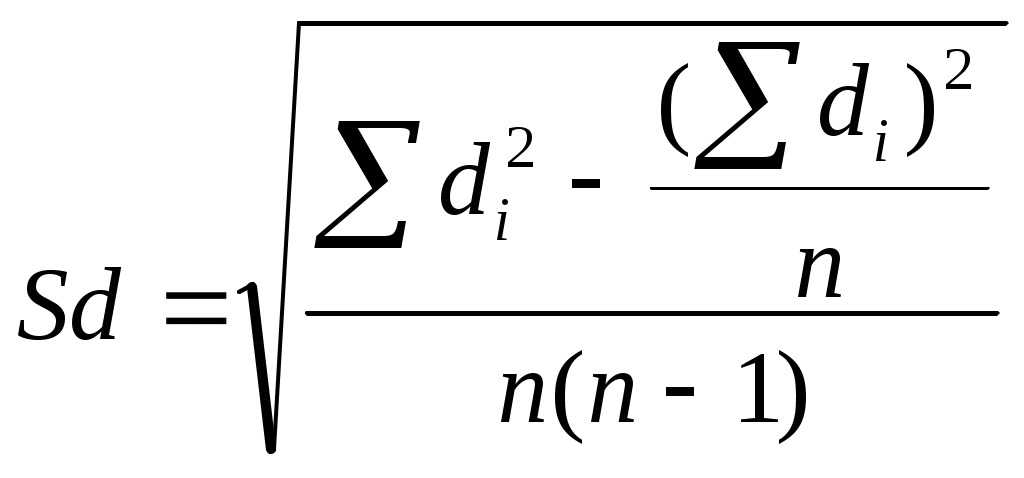
Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок.

Если tэмп
Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест.





До эксперимента
После эксперимента
d
d2

1
14
18
4
16

2
20
19
-1
1

3
15
22
7
49

4
11
17
6
36

5
16
24
8
64

6
13
21
8
64

7
16
25
9
81

8
19
26
7
49

9
15
24
9
81

10
9
15
6
36

Сумма
148
211
63
477


d=63/10=6,3


=6,678
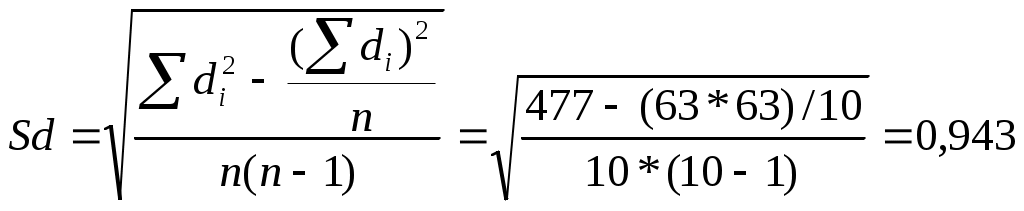
Число степеней свободы: k=10-1=9 и по таблице приложения находим tкрит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтернативной гипотезы (H1) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.

В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Н0 отклоняется и принимается гипотеза Н1

Смотрите также файлы