Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 496
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РАЗДЕЛ III. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
В данной таблице приведены основные методы, использующиеся в биологических исследованиях, в зависимости от задач исследователя. В следующих главах мы постараемся подробно описать области применения, способ расчета и интерпретацию получаемых результатов.
Проверка гипотезы о законе распределения
Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими.
Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически - формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения
Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению. Может проводиться и сравнение частостей.
Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о биномиальном распределении, распределении Пуассона и т.д. Причина частого обращения к нормальному распределению в том, что в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из них не имеет преобладающего влияния. Закон нормального распределения лежит в основе многих теорем математической статистики, применяемых для оценки репрезентативности выборок, при измерении связей и т. д.
Итак, пусть имеется вариационный ряд. Предположим, что признак Х распределен по некоторому вероятностному закону Р.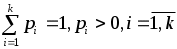
По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты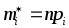 . Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
. Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
χ2 Пирсона
Критерий согласия χ2 разработан достаточно хорошо и поэтому используется достаточно часто. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.
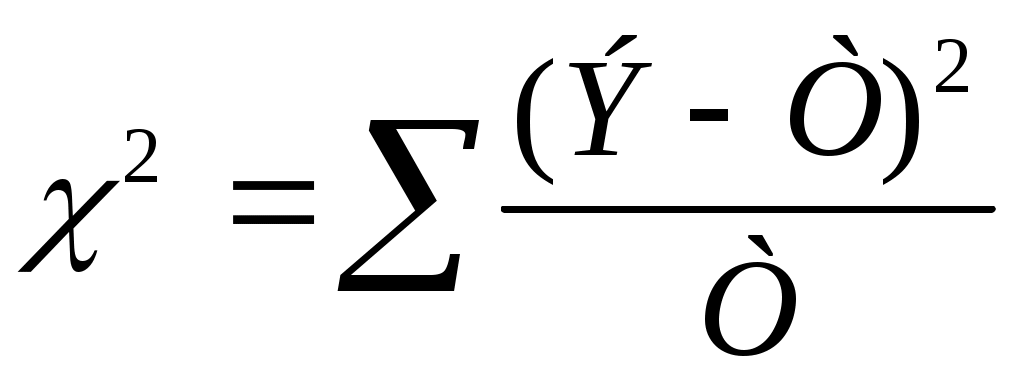
Если все эмпирические частоты равны соответствующим теоретическим частотам, то χ2
равно нулю. Очевидно, что чем больше отличаются эмпирические и теоретические частоты, тем χ2 больше; если расхождение несущественно, то χ2 должно быть малым.
Гипотезы -
Н0: Различия между двумя распределениями недостоверны.
H1: Различия между двумя распределениями достоверны.
Существуют табличные значения (см. приложение) для соответствующего числа степеней свободы К и уровня значимости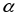 . По таблице находятся
. По таблице находятся 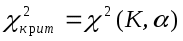 K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.
K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.
λ - критерий Колмогорова-Смирнова
Назначение критерия
Критерий λпредназначен для сопоставления двух распределений:
а) эмпирического с теоретическим, например, равномерным или нормальным;
б) одного эмпирического распределения с другим эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если в методе χ2 мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Гипотезы -
Н0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
H1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λ включается эта разность. Чем больше эмпирическое значение λ, тем более существенны различия.
Описательные статистики
Концепция сжатия экспериментальных данных
Графическое представление всей совокупности экспериментальных данных позволяет многими способами осмыслить длинные ряды наблюдений. Тем не менее, построение графиков и таблиц представляет собой только первый шаг при статистическом анализе данных. Следующий шаг — представление результатов в компактной форме, удобной для хранения, сопоставления с другими данными и т. д. При
этом желательно, чтобы характерные особенности распределения численностей выражались небольшим числом показателей.
Графические представления распределения численностей, рассмотренные нами ранее, очень существенно отличаются друг от друга. Однако у всех этих графиков существуют и общие характерные особенности, которые позволяют их сравнивать между coбой.
Прежде всего, видно, что все распределения группируются относительно некоторого центра. Для измерения положения этого центра существует группа показателей, носящих название мер центральной тенденции. К ним относятся средние (среднее арифметически среднее геометрическое, среднее гармоническое), мода и медиана.
Другой характерной особенностью распределений численностей является разброс экспериментальных значений относительно центра распределения. Количественная оценка этого разброса осуществляется с помощью мер рассеяния, важнейшими из которых являются размах, дисперсия, среднеквадратическое отклонение и коэффициент вариации.
Визуальный анализ графических изображений показывает, что некоторые распределения асимметричны, т. е. по обе стороны от центра расположено неравное количество значений, причем асимметрия может быть как право-, так и левосторонней. Наконец, графики некоторых распределений более заострены, а других — уплощены. Эти характерные особенности распределений экспериментальных данных — скошенность и островершинность — также могут быть описаны с помощью показателей асимметрии и эксцесса (островершинности).
Оказывается, что для описания практически любого встречающегося на практике распределения численностей достаточно этих четырех групп мер: показателей центральной тенденции, показателей рассеяния (вариации), показателей асимметрии, показателей эксцесса, вся совокупность которых получила название «статистик свертки».
Показатели центральной тенденции. Средние.
В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую группу одним (средним) числом.
В зависимости от того, как распределены исходные данные - в равно- или неравноинтервальный вариационный ряд, для их характеристики применяют разные средние величины. Именно при распределении собранных данных в неравноинтервальный вариационный ряд более подходящей обобщающей характеристикой изучаемого объекта служит так называемая плотность распределения, т. е. отношение частот или частостей к ширине классовых интервалов. Кроме того, числовыми характеристиками таких рядов могут служить средние из абсолютных или относительных показателей плотности распределения. Средняя плотность показывает, сколько единиц данной совокупности приходится в среднем на интервал, равный единице измерения учитываемого признака.
В качестве статистических характеристик равноинтервальных вариационных рядов применяют средние величины.
Средняя арифметическая. Этот показатель является центром распределения, вокруг которого группируются все варианты статистической совокупности. Средняя арифметическая может быть простой и взвешенной. Простую арифметическую определяют как сумму всех членов совокупности, деленную на их общее число.
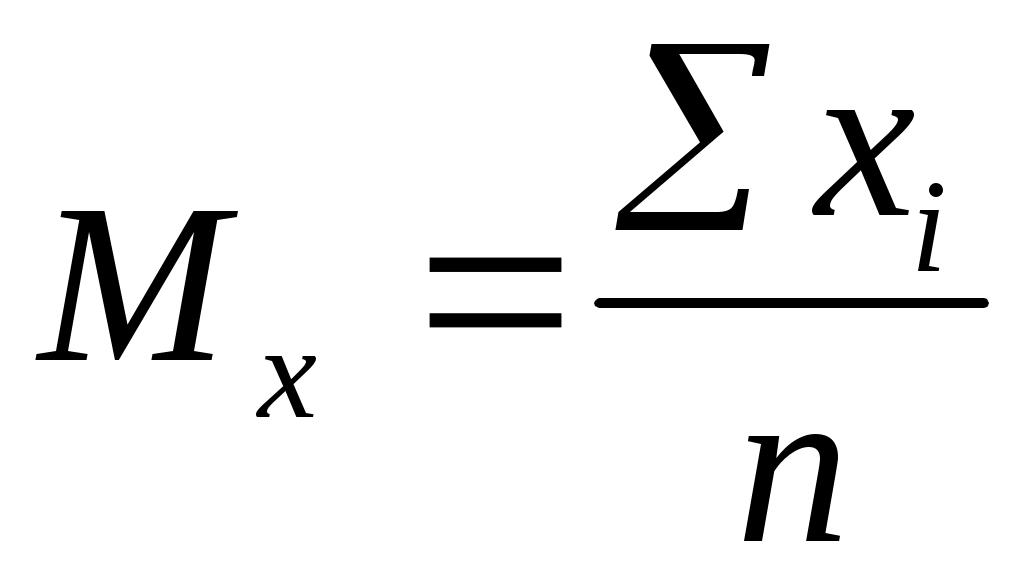
Когда отдельные варианты повторяются, среднюю арифметическую вычисляют по формуле: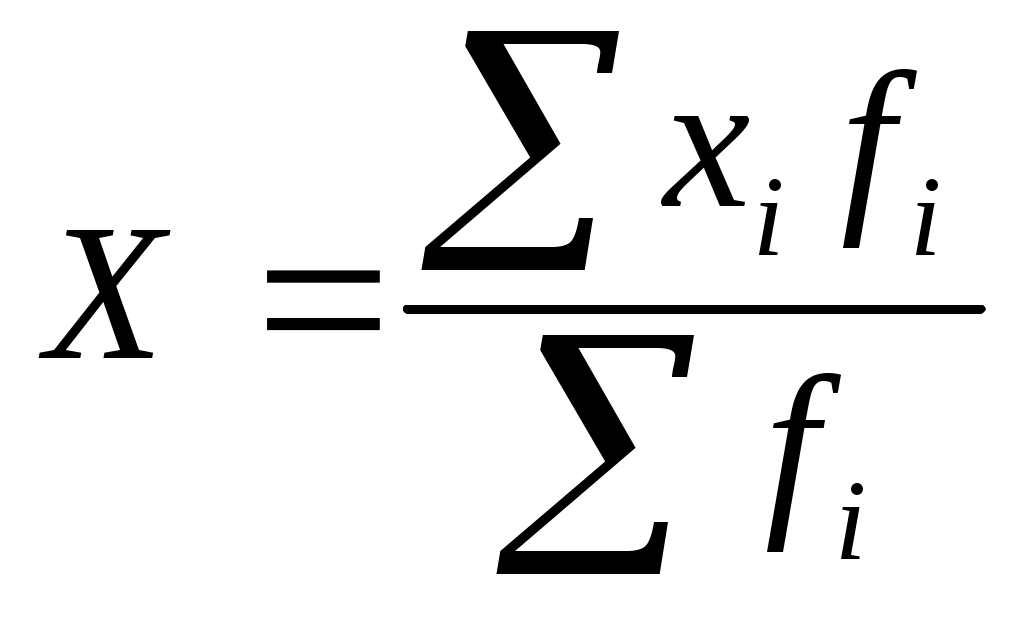 и называют взвешенной средней.
и называют взвешенной средней.
Имеется распределение учета численности косуль за апрель 2003г. Требуется вычислить среднее количество косуль за учет.
X=(7+20+12+12+15)/30=66/30=2.02.
В биологических науках среднюю арифметическую принято обозначать как М.
Средняя арифметическая обладает рядом важных свойств.
1. Если каждую варианту статистической совокупности уменьшить или увеличить на некоторое произвольно взятое положительное число, то и средняя уменьшится или увеличится на это число.
2. Если каждую варианту разделить или умножить на какое-то одно и то же число, то и средняя арифметическая изменится во столько же раз.
3. Сумма произведений отклонений вариант от их средней арифметической на соответствующие им частоты равна нулю.
4. Сумма квадратов отклонений вариант от их средней меньше суммы квадратов отклонений тех же вариант от любой другой величины.
Это свойство среднего имеет приложения в приближенных решениях задач следующего вида. Допустим, на основании достаточно обширного экспериментального материала известны средние характеристики одного и того вида животных или растений, занимающих разные экологические ниши. Экземпляры из разных мест обитания будут
| Задача | Количественные переменные, имеющие нормальное распределение | Количественные и порядковые переменные | Качественные переменные |
| Описательные статистики | MS или Mm | Me, 25 и 75 персентиль | % |
| Сравнение двух независимых выборок | Т критерий | U критерий Манна-Уитни | Тест Фишера, 2 |
| Сравнение более двух независимых выборок | Дисперсионный анализ Фишера | Дисперсионный анализ Краскел-Уоллиса | 2 |
| Сравнение двух зависимых выборок | Парный Т критерий | Критерий Вилкоксона | Тест Мак-Немара |
| Изучение взаимосвязи между признаками | Коэффициент корреляции Пирсона | Коэффициент корреляции Спирмена | 2 |
| Предсказать изменение одного значения, если было измерено другое значение | Простая линейная или нелинейная регрессия | Непараметрическая регрессия | Простая логистическая регрессия |
В данной таблице приведены основные методы, использующиеся в биологических исследованиях, в зависимости от задач исследователя. В следующих главах мы постараемся подробно описать области применения, способ расчета и интерпретацию получаемых результатов.
Проверка гипотезы о законе распределения
Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими.
Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически - формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения
Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению. Может проводиться и сравнение частостей.
Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о биномиальном распределении, распределении Пуассона и т.д. Причина частого обращения к нормальному распределению в том, что в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из них не имеет преобладающего влияния. Закон нормального распределения лежит в основе многих теорем математической статистики, применяемых для оценки репрезентативности выборок, при измерении связей и т. д.
Итак, пусть имеется вариационный ряд. Предположим, что признак Х распределен по некоторому вероятностному закону Р.
| х | х1 | х2 | .... | xk |
| р | p1 | p2 | ..... | pk |
По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты
χ2 Пирсона
Критерий согласия χ2 разработан достаточно хорошо и поэтому используется достаточно часто. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.
Если все эмпирические частоты равны соответствующим теоретическим частотам, то χ2
равно нулю. Очевидно, что чем больше отличаются эмпирические и теоретические частоты, тем χ2 больше; если расхождение несущественно, то χ2 должно быть малым.
Гипотезы -
Н0: Различия между двумя распределениями недостоверны.
H1: Различия между двумя распределениями достоверны.
Существуют табличные значения (см. приложение) для соответствующего числа степеней свободы К и уровня значимости
λ - критерий Колмогорова-Смирнова
Назначение критерия
Критерий λпредназначен для сопоставления двух распределений:
а) эмпирического с теоретическим, например, равномерным или нормальным;
б) одного эмпирического распределения с другим эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если в методе χ2 мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Гипотезы -
Н0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
H1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λ включается эта разность. Чем больше эмпирическое значение λ, тем более существенны различия.
Описательные статистики
Концепция сжатия экспериментальных данных
Графическое представление всей совокупности экспериментальных данных позволяет многими способами осмыслить длинные ряды наблюдений. Тем не менее, построение графиков и таблиц представляет собой только первый шаг при статистическом анализе данных. Следующий шаг — представление результатов в компактной форме, удобной для хранения, сопоставления с другими данными и т. д. При
этом желательно, чтобы характерные особенности распределения численностей выражались небольшим числом показателей.
Графические представления распределения численностей, рассмотренные нами ранее, очень существенно отличаются друг от друга. Однако у всех этих графиков существуют и общие характерные особенности, которые позволяют их сравнивать между coбой.
Прежде всего, видно, что все распределения группируются относительно некоторого центра. Для измерения положения этого центра существует группа показателей, носящих название мер центральной тенденции. К ним относятся средние (среднее арифметически среднее геометрическое, среднее гармоническое), мода и медиана.
Другой характерной особенностью распределений численностей является разброс экспериментальных значений относительно центра распределения. Количественная оценка этого разброса осуществляется с помощью мер рассеяния, важнейшими из которых являются размах, дисперсия, среднеквадратическое отклонение и коэффициент вариации.
Визуальный анализ графических изображений показывает, что некоторые распределения асимметричны, т. е. по обе стороны от центра расположено неравное количество значений, причем асимметрия может быть как право-, так и левосторонней. Наконец, графики некоторых распределений более заострены, а других — уплощены. Эти характерные особенности распределений экспериментальных данных — скошенность и островершинность — также могут быть описаны с помощью показателей асимметрии и эксцесса (островершинности).
Оказывается, что для описания практически любого встречающегося на практике распределения численностей достаточно этих четырех групп мер: показателей центральной тенденции, показателей рассеяния (вариации), показателей асимметрии, показателей эксцесса, вся совокупность которых получила название «статистик свертки».
Показатели центральной тенденции. Средние.
В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую группу одним (средним) числом.
В зависимости от того, как распределены исходные данные - в равно- или неравноинтервальный вариационный ряд, для их характеристики применяют разные средние величины. Именно при распределении собранных данных в неравноинтервальный вариационный ряд более подходящей обобщающей характеристикой изучаемого объекта служит так называемая плотность распределения, т. е. отношение частот или частостей к ширине классовых интервалов. Кроме того, числовыми характеристиками таких рядов могут служить средние из абсолютных или относительных показателей плотности распределения. Средняя плотность показывает, сколько единиц данной совокупности приходится в среднем на интервал, равный единице измерения учитываемого признака.
В качестве статистических характеристик равноинтервальных вариационных рядов применяют средние величины.
Средняя арифметическая. Этот показатель является центром распределения, вокруг которого группируются все варианты статистической совокупности. Средняя арифметическая может быть простой и взвешенной. Простую арифметическую определяют как сумму всех членов совокупности, деленную на их общее число.
Когда отдельные варианты повторяются, среднюю арифметическую вычисляют по формуле:
Имеется распределение учета численности косуль за апрель 2003г. Требуется вычислить среднее количество косуль за учет.
| Число косуль | 0 | 1 | 2 | 3 | 4 | 5 | Итого 30 |
| Число учетов | 3 | 7 | 10 | 4 | 3 | 3 | |
X=(7+20+12+12+15)/30=66/30=2.02.
В биологических науках среднюю арифметическую принято обозначать как М.
Средняя арифметическая обладает рядом важных свойств.
1. Если каждую варианту статистической совокупности уменьшить или увеличить на некоторое произвольно взятое положительное число, то и средняя уменьшится или увеличится на это число.
2. Если каждую варианту разделить или умножить на какое-то одно и то же число, то и средняя арифметическая изменится во столько же раз.
3. Сумма произведений отклонений вариант от их средней арифметической на соответствующие им частоты равна нулю.
4. Сумма квадратов отклонений вариант от их средней меньше суммы квадратов отклонений тех же вариант от любой другой величины.
Это свойство среднего имеет приложения в приближенных решениях задач следующего вида. Допустим, на основании достаточно обширного экспериментального материала известны средние характеристики одного и того вида животных или растений, занимающих разные экологические ниши. Экземпляры из разных мест обитания будут