ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 555
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
шипные (рис.4.1, а); коленчатые (рис.4.1, б); гибкие (рис.4.1, в); телескопические (рис.4.1, г); карданные (рис.4.1, д).
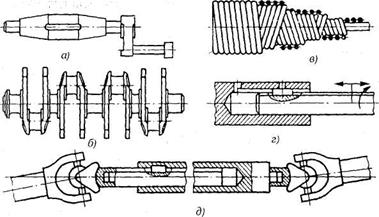
Рис.4.1. Типы валов: а — кривошипный вал; б — коленчатый вал; в — гибкий вал;
г — телескопический вал; д — карданный вал
Посадочные поверхности валов и осей под ступицы насаживаемых деталей называютцапфамии выполняют для валов работающих с подшипниками скольжения цилиндрическими, коническими, шаровыми или с буртами (рис.6). При этом принято называть промежуточные цапфы шейками, концевые — шипами(рис.5.2).
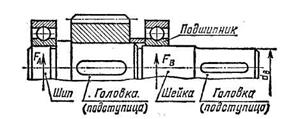
Рис. 5.2. Цапфы
Расчетные схемы валов и осей
Для расчета валов и осей на прочность и жесткость составляют расчетную схему. При переходе от конструкции к расчетной схеме производят схематизацию нагрузок, опор и формы вала.
При составлении расчетных схем принимают, что установленные на осях и валах детали передают им силы и моменты посередине свой ширины. В расчетах осей и валов на прочность и жесткость их собственный вес и вес расположенных на них деталей (за исключением маховиков), а также силы трения, возникающие в опорах, не учитываются.
На рис. 7.2 вал нагружен силами: окружной силой Ft, радиальной силой Fr, осевой силой Fa, силой от муфты FM.
Эти силы действуют в двух взаимно перпендикулярных плоскостях. Изобразим их в вертикальной и горизонтальной плоскости и приведем к оси вала.
После приведения сил к оси вала возникают изгибающий момент и крутящий момент . Здесь d - делительный диаметр колеса.
Строим эпюры изгибающих моментов в вертикальной My и горизонтальной плоскости Mx, эпюру суммарных изгибающих моментов M и эпюру крутящих моментов T.
Суммарный изгибающий момент определяется по зависимости
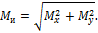
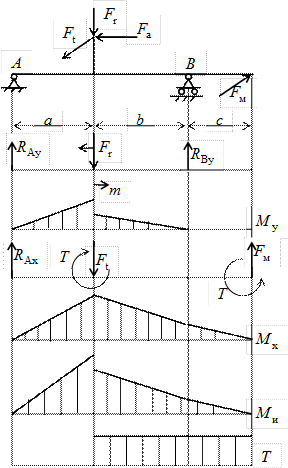
Рис.7.2. Пример расчетной схемы вала
Последовательность проектировочного расчета.
По конструкции узла (рис.9, а) составляют расчетную схему (рис.9, б), определяют силы, действующие на ось, строят эпюры изгибающих моментов; диаметр оси d определяют по формуле
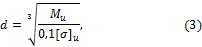
где Ми — максимальный изгибающий момент; — допускаемое напряжение изгиба.
Приближенный расчет валов на прочность
При этом методе расчета различие характера циклов изменения нормальных и касательных напряжений и их влияние на прочность не учитывают.
В зависимости от действия нагрузок возможны два случая приближенного расчета валов на прочность: расчет только на кручение и расчет на совместное действие кручения и изгиба.
Приближенный расчет выполняют как проектировочный, на основе которого ориентировочно устанавливают диаметры характерных сечений вала с последующим уточнением коэффициентов запаса прочности по выносливости (уточненный расчет см. ниже).
Расчет валов на кручение.
При этом расчете обычно определяют диаметр выходного конца вала или диаметр вала под подшипником (под опорой), который испытывает только кручение.
Исходя из условия прочности (1) выполняют проектировочный расчет

и проверочный расчет
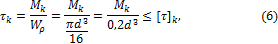
где d — расчетный диаметр вала; Мк— крутящий момент вопасном сечении вала; и — расчетное и допускаемое напряжения кручения в опасном сечении вала (для сталей 45 и Ст5 = 25 35 МПа).
Расчет валов на совместное действие кручения и изгиба.
Большинство валов работают на изгиб и кручение. Кроме этого некоторые участки вала под действием осевых сил могут дополнительно работать на растяжение или сжатие. Однако эти напряжения невелики по сравнению с [σ]
u и их обычно не учитывают.
Для расчета вала на сложное сопротивление необходимо знать величины Mu в опасных сечениях. С этой целью по предварительно принятому или рассчитанному диаметру вала намечают местоположение опор и составляют расчетную схему, определяют все силы, действующие на вал, строят эпюрыMuи Mk, намечают опасные сечения, а затем производят расчет вала.
Результирующие опорные реакции Ri и результирующие изгибающие моменты определяют по формулам:
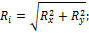
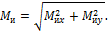
где Rx; Ry; Mux; Muy – соответственно опорные реакции и изгибающие моменты во взаимно перпендикулярных плоскостях.
Участок вала между опорами (под шестерней, колесом и т.п.) рассчитывают на совместное действие кручения и изгиба по эквивалентному моменту Мэкв.
Эквивалентный момент вычисляют обычно по формуле (при расчете по теории максимальных касательных напряжений):
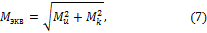
где Ми и Мк— изгибающий и крутящий моменты.
По аналогии с рассмотренными выше случаями расчета выполняют:
проектировочный расчет

и проверочный расчет
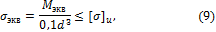
где — эквивалентное напряжение для расчетного сечения вала.
Получив расчетным путем размеры, с учетом технологии изготовления проектируют конструктивную форму вала.
Приближенный расчет на совместное действие кручения и изгиба для неответственных конструкций валов можно считать основным. Уточненный расчет на выносливость можно не производить, если соблюдается условие
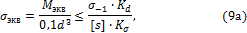
где — предел выносливости материала при изгибе (симметричный цикл); Kd— масштабный коэффициент; — эффективный коэффициент концентрации напряжений в опасном сечении
; [s] — допускаемый коэффициент запаса прочности по выносливости.
Уточненный расчет валов (осей) на выносливость
При расчете вращающихся осей и валов на выносливость учитывают все основные факторы, влияющие на усталостную прочность: характер изменения напряжений, статические и усталостные характеристики материалов, изменение предела выносливости вследствие концентрации напряжений и влияние абсолютных размеров осей или валов, состояние поверхности. Для учета всех этих факторов конструкция вала должна быть известна.
Усталостная прочность вала (оси) обеспечена, если соблюдается условие
где s и [s] — фактический (расчетный) и допускаемый коэффициенты запаса прочности для опасного сечения; (обычно [s] = 1,5...2,5; для валов передач [s]> 1,7...3).
При расчете на усталостную прочность необходимо установить характер цикла изменения напряжений. В большинстве случаев действительный цикл нагрузки машин в эксплуатационных условиях установить трудно. При расчете валов (осей) на усталостную прочность принимают, что напряжения изгиба изменяются по симметричному циклу (рис.12, а), а напряжения кручения — по пульсирующему (отнулевому) циклу (рис.12, б).
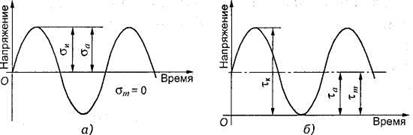
Рис.12. Циклы изменений напряжений в сечениях вала: а — симметричный цикл (напряжения изгиба);
б— отнулевой цикл (напряжения кручения)
Для опасных сечений определяют коэффициенты запаса сопротивления усталости и сравнивают их с допускаемыми. При одновременном действии напряжений изгиба и кручения коэффициент запаса сопротивления усталости определяют по формуле
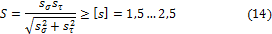
где – коэффициент запаса сопротивления усталости по нормальным напряжениям при изгибе
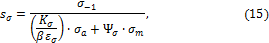
– коэффициент запаса сопротивления усталости по касательным напряжениям при кручении
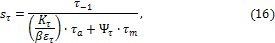
В этих формулах и – пределы выносливости соответственно при изгибе и при кручении при симметричном цикле изменения напряжений. Это характеристики материала, которые выбираются по справочникам или по приближенным формулам:
и – амплитуды переменных составляющих циклов напряжений;
и – средние напряжения циклов соответственно при изгибе и кручении.
Последовательность расчета валов и осей на усталостную прочность (выносливость).
1. Составляют расчетную схему.
2. Определяют силы, действующие на вал.
3. Определяют опорные реакции и строят эпюры изгибающих моментов в двух взаимно перпендикулярных плоскостях, после чего вычисляют суммарный изгибающий момент.
4. Определяют крутящие моменты и строят эпюру (для валов).
5. По формуле (9а) определяют эквивалентный момент Мэкв.
6. В соответствии с эпюрами моментов Мп, Мк иМэкв рассчитывают диаметры опасных сечений, подлежащих проверке на усталостную прочность.
7. Для каждого опасного сечения по формуле (13) определяют расчетные коэффициенты запаса прочности, а по формуле (14) оценивают выносливость.
8. При кратковременных перегрузках наиболее нагруженные сечения вала проверяют на статическую прочность (по теории энергии формоизменения):
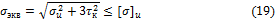
Расчет валов на колебания
Для большинства быстроходных валов причинами, вызывающими колебания являются силы от неуравновешенных масс деталей. При совпадении или кратности частоты возмущающей силы и частоты собственных колебаний вала наступает явление резонанса, при котором амплитуда колебаний вала резко возрастает и может достигнуть опасных значений. Соответствующие резонансу угловую скорость (ω) и частоту вращения (n) называют критическими (ωкр, nкр).
Различают следующие виды колебаний валов: поперечные или изгибные угловые или крутильные; и изгибно-крутильные. В курсе ДМ рассматривают только поперечные колебания, а остальные – в специальных курсах.

Рис.4.1. Типы валов: а — кривошипный вал; б — коленчатый вал; в — гибкий вал;
г — телескопический вал; д — карданный вал
Посадочные поверхности валов и осей под ступицы насаживаемых деталей называютцапфамии выполняют для валов работающих с подшипниками скольжения цилиндрическими, коническими, шаровыми или с буртами (рис.6). При этом принято называть промежуточные цапфы шейками, концевые — шипами(рис.5.2).

Рис. 5.2. Цапфы
Расчетные схемы валов и осей
Для расчета валов и осей на прочность и жесткость составляют расчетную схему. При переходе от конструкции к расчетной схеме производят схематизацию нагрузок, опор и формы вала.
При составлении расчетных схем принимают, что установленные на осях и валах детали передают им силы и моменты посередине свой ширины. В расчетах осей и валов на прочность и жесткость их собственный вес и вес расположенных на них деталей (за исключением маховиков), а также силы трения, возникающие в опорах, не учитываются.
На рис. 7.2 вал нагружен силами: окружной силой Ft, радиальной силой Fr, осевой силой Fa, силой от муфты FM.
Эти силы действуют в двух взаимно перпендикулярных плоскостях. Изобразим их в вертикальной и горизонтальной плоскости и приведем к оси вала.
После приведения сил к оси вала возникают изгибающий момент и крутящий момент . Здесь d - делительный диаметр колеса.
Строим эпюры изгибающих моментов в вертикальной My и горизонтальной плоскости Mx, эпюру суммарных изгибающих моментов M и эпюру крутящих моментов T.
Суммарный изгибающий момент определяется по зависимости

Рис.7.2. Пример расчетной схемы вала
Последовательность проектировочного расчета.
По конструкции узла (рис.9, а) составляют расчетную схему (рис.9, б), определяют силы, действующие на ось, строят эпюры изгибающих моментов; диаметр оси d определяют по формуле
где Ми — максимальный изгибающий момент; — допускаемое напряжение изгиба.
Приближенный расчет валов на прочность
При этом методе расчета различие характера циклов изменения нормальных и касательных напряжений и их влияние на прочность не учитывают.
В зависимости от действия нагрузок возможны два случая приближенного расчета валов на прочность: расчет только на кручение и расчет на совместное действие кручения и изгиба.
Приближенный расчет выполняют как проектировочный, на основе которого ориентировочно устанавливают диаметры характерных сечений вала с последующим уточнением коэффициентов запаса прочности по выносливости (уточненный расчет см. ниже).
Расчет валов на кручение.
При этом расчете обычно определяют диаметр выходного конца вала или диаметр вала под подшипником (под опорой), который испытывает только кручение.
Исходя из условия прочности (1) выполняют проектировочный расчет
и проверочный расчет
где d — расчетный диаметр вала; Мк— крутящий момент вопасном сечении вала; и — расчетное и допускаемое напряжения кручения в опасном сечении вала (для сталей 45 и Ст5 = 25 35 МПа).
Расчет валов на совместное действие кручения и изгиба.
Большинство валов работают на изгиб и кручение. Кроме этого некоторые участки вала под действием осевых сил могут дополнительно работать на растяжение или сжатие. Однако эти напряжения невелики по сравнению с [σ]
u и их обычно не учитывают.
Для расчета вала на сложное сопротивление необходимо знать величины Mu в опасных сечениях. С этой целью по предварительно принятому или рассчитанному диаметру вала намечают местоположение опор и составляют расчетную схему, определяют все силы, действующие на вал, строят эпюрыMuи Mk, намечают опасные сечения, а затем производят расчет вала.
Результирующие опорные реакции Ri и результирующие изгибающие моменты определяют по формулам:
где Rx; Ry; Mux; Muy – соответственно опорные реакции и изгибающие моменты во взаимно перпендикулярных плоскостях.
Участок вала между опорами (под шестерней, колесом и т.п.) рассчитывают на совместное действие кручения и изгиба по эквивалентному моменту Мэкв.
Эквивалентный момент вычисляют обычно по формуле (при расчете по теории максимальных касательных напряжений):
где Ми и Мк— изгибающий и крутящий моменты.
По аналогии с рассмотренными выше случаями расчета выполняют:
проектировочный расчет
и проверочный расчет
где — эквивалентное напряжение для расчетного сечения вала.
Получив расчетным путем размеры, с учетом технологии изготовления проектируют конструктивную форму вала.
Приближенный расчет на совместное действие кручения и изгиба для неответственных конструкций валов можно считать основным. Уточненный расчет на выносливость можно не производить, если соблюдается условие
где — предел выносливости материала при изгибе (симметричный цикл); Kd— масштабный коэффициент; — эффективный коэффициент концентрации напряжений в опасном сечении
; [s] — допускаемый коэффициент запаса прочности по выносливости.
Уточненный расчет валов (осей) на выносливость
При расчете вращающихся осей и валов на выносливость учитывают все основные факторы, влияющие на усталостную прочность: характер изменения напряжений, статические и усталостные характеристики материалов, изменение предела выносливости вследствие концентрации напряжений и влияние абсолютных размеров осей или валов, состояние поверхности. Для учета всех этих факторов конструкция вала должна быть известна.
Усталостная прочность вала (оси) обеспечена, если соблюдается условие
где s и [s] — фактический (расчетный) и допускаемый коэффициенты запаса прочности для опасного сечения; (обычно [s] = 1,5...2,5; для валов передач [s]> 1,7...3).
При расчете на усталостную прочность необходимо установить характер цикла изменения напряжений. В большинстве случаев действительный цикл нагрузки машин в эксплуатационных условиях установить трудно. При расчете валов (осей) на усталостную прочность принимают, что напряжения изгиба изменяются по симметричному циклу (рис.12, а), а напряжения кручения — по пульсирующему (отнулевому) циклу (рис.12, б).

Рис.12. Циклы изменений напряжений в сечениях вала: а — симметричный цикл (напряжения изгиба);
б— отнулевой цикл (напряжения кручения)
Для опасных сечений определяют коэффициенты запаса сопротивления усталости и сравнивают их с допускаемыми. При одновременном действии напряжений изгиба и кручения коэффициент запаса сопротивления усталости определяют по формуле
где – коэффициент запаса сопротивления усталости по нормальным напряжениям при изгибе
– коэффициент запаса сопротивления усталости по касательным напряжениям при кручении
В этих формулах и – пределы выносливости соответственно при изгибе и при кручении при симметричном цикле изменения напряжений. Это характеристики материала, которые выбираются по справочникам или по приближенным формулам:
и – амплитуды переменных составляющих циклов напряжений;
и – средние напряжения циклов соответственно при изгибе и кручении.
Последовательность расчета валов и осей на усталостную прочность (выносливость).
1. Составляют расчетную схему.
2. Определяют силы, действующие на вал.
3. Определяют опорные реакции и строят эпюры изгибающих моментов в двух взаимно перпендикулярных плоскостях, после чего вычисляют суммарный изгибающий момент.
4. Определяют крутящие моменты и строят эпюру (для валов).
5. По формуле (9а) определяют эквивалентный момент Мэкв.
6. В соответствии с эпюрами моментов Мп, Мк иМэкв рассчитывают диаметры опасных сечений, подлежащих проверке на усталостную прочность.
7. Для каждого опасного сечения по формуле (13) определяют расчетные коэффициенты запаса прочности, а по формуле (14) оценивают выносливость.
8. При кратковременных перегрузках наиболее нагруженные сечения вала проверяют на статическую прочность (по теории энергии формоизменения):
Расчет валов на колебания
Для большинства быстроходных валов причинами, вызывающими колебания являются силы от неуравновешенных масс деталей. При совпадении или кратности частоты возмущающей силы и частоты собственных колебаний вала наступает явление резонанса, при котором амплитуда колебаний вала резко возрастает и может достигнуть опасных значений. Соответствующие резонансу угловую скорость (ω) и частоту вращения (n) называют критическими (ωкр, nкр).
Различают следующие виды колебаний валов: поперечные или изгибные угловые или крутильные; и изгибно-крутильные. В курсе ДМ рассматривают только поперечные колебания, а остальные – в специальных курсах.