Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 234
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Табличные значения критерия Стьюдента
Уровень статистической значимости.
= 0,05.
Степень свободы
f = N(m-1) = 8*(5-1) = 32
Вывод. Табличное значение критерия Стьюдента tт= 2,04. Элемент b12x1x2; b13x1x2, статистически незначим, может быть исключен.
Функция отклика со статистически значимыми коэффициентами.
Y = b0+b1X1+ b2X2 + b3X3 - b23X2 X3+b123X1 X2X3
Y = 5,86+0,27X1+0,50X2+1,05X3 -0,036X2 X3 +0,233X1X2X3
Значения функции отклика для каждого опыта по новой функции отклика со статистически значимыми коэффициентами.
Подставив значения Х из матрицы планирования в функцию отклика и подсчитав, получим средние значения Y’ для каждого опыта.
| Номер опыта | Y’ | Yср |
| 1 | 9,31 | 4,60 |
| 2 | 10,32 | 4,75 |
| 3 | 11,50 | 4,37 |
| 4 | 11,58 | 5,52 |
| 5 | 12,60 | 5,60 |
| 6 | 12,67 | 6,48 |
| 7 | 12,40 | 7,76 |
| 8 | 13,41 | 7,77 |
Проверка адекватности новой функции отклика со статистически значимыми коэффициентами
Расчетное значение критерия Фишера.
Адекватность модели проверяют по критерию Фишера F- критерию, расчетное значение которого определяется по формуле:
Fp= S2ад/S2в ;
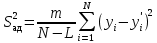 ;
;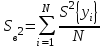 ,
,где S2
ад - дисперсия адекватности;
S2в - дисперсия воспроизводимости, характеризующая точность одного измерения, является средняя из всех построчных дисперсий;
L – число значимых коэффициентов
Для удобства составим таблицу разности Yср – Y’:
| Номер опыта | Ycp-Y’ |
| 1 | -4,704 |
| 2 | -5,571 |
| 3 | -7,124 |
| 4 | -6,052 |
| 5 | -6,989 |
| 6 | -6,186 |
| 7 | -4,634 |
| 8 | -5,641 |
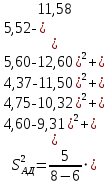
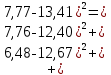 702,3
702,3S2в =
 = 0,0375.
= 0,0375.Fp =
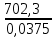 = 18728.
= 18728.Уровень значимости = 0,05.
Степень свободы адекватности:
Определяем число степеней свободы
fад = N-L= 8-6 = 2
Степень свободы воспроизводимости:
fв = N(m-1) = 8*(5-1) = 32.
Табличное значение критерия Фишера.
Fт = 3,3
Fp > Fт, следовательно полученная математическая модель с принятым уровнем статистической значимости не адекватна экспериментальным данным.
Функция отклика со статистически значимыми коэффициентами и натуральными факторами
Y = b0+b1X1+ b2X2 + b3X3 - b23X2 X3+b123X1 X2X3
Перейдем к натуральным факторам
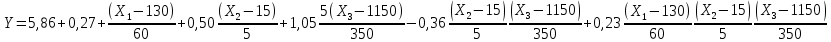
Заключение
В ходе практической работы была построена целевая функция, характеризующая зависимость износа долота от трёх факторов: количество оборотов ротора, осевая нагрузка на долото и плотность бурового раствора. За основу целевой функции была принята полиноминальная регрессионная модель.
В результате проведенной работы, полученная модель позволила получить средние значения Y’ практические равные Y, что означает ее правильность и означает, что работа выполнена верно.
Литература
-
Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399 с. -
Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479 с. -
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476 с. -
Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с. (электронный ресурс). -
Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976. -
Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983. -
Налимов В.В. Теория эксперимента. М.: Наука, 1971. -
Планирование и организация измерительного эксперимента / Е.Т. Володарский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987.