Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра нефтегазового дела

Контрольная работа

по дисциплине

«СТАТИСТИЧЕСКИЙ АНАЛИЗ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА»


Вариант №42


Выполнил:

студент группы НДбз-18-2

Носков В.А

Проверил преподаватель:

Шмаков А. К.


Иркутск 2022 г.

1 СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН
1.1. Статистический анализ одномерной последовательности случайных величин
Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин.
Задание:

1. 
   Подготовить исходные данные.
   
2. 
   Построить вариационный, статистический, группированный ряды.
   
3. 
   Построить гистограмму, полигон, кумуляту, огиву.
   
4. 
   Определить относительные частоты последовательности.
   
5. 
   Определить: среднее арифметическое (по вариационному ряду), средневзвешенное (по группированному ряду), моду, медиану, дисперсию (по группированному ряду); среднее квадратическое отклонение, коэффициент вариации.
   
6. 
   Рассчитать в программе Excel характеристики описательной статистики для заданной последовательности случайных величин.
   

1. 
   Исходные данные
   

В качестве исходных данных принято количество агрегатов в работе, таблица 1.1.
Таблица 1.1- Кпес. - песчанистость,

Ккар

карбонатность.

№ п.п. Ккар% Кпес. % 12 81 13,2 66 12 54 7 76 13 52 11 81 11 48 10 74 9 28 10 80 12 51 13 50 13 51 13 54 19 55 13 52 13 82 13 85 12 81 13,2 66 12 54 7 76 13 52 11 81 11 48

10 74 9 28 10 80 12 51 13 50 13 51 13 54 19 55 13 52 13 82 13 85 12 81 13,2 66 12 54 7 76 13 52 11 81 11 48 10 74 9 28 10 80 12 51 13 50 13 51 13 54 19 55

---

Средствами программы Excel рассчитаны характеристики описательной статистики заданной последовательности значений случайной величины, числовые значения которых приведены на рисунке 1.1.

Среднее	12,01176
Стандартная ошибка	0,343747
Медиана	12
Мода	13
Стандартное отклонение	2,454844
Дисперсия выборки	6,026259
Эксцесс	2,661977
Асимметричность	0,747956
Интервал	12
Минимум	7
Максимум	19
Сумма	612,6
Счет	51

Рисунок 1.1 – Характеристики описательной статистики случайной величины

2. 
   Вариационный ряд
   

Вариационный ряд – последовательность, записанная в возрастающем порядке

Для заданной последовательности случайных величин вариационный ряд показан в таблице 1.2.


Таблица 1.2- Карбонатность %.

№ п/п	Ккар%	№ п/п	Ккар%
1	12	27	9
2	13,2	28	10
3	12	29	12
4	7	30	13
5	13	31	13
6	11	32	13
7	11	33	19
8	10	34	13
9	9	35	13
10	10	36	13
11	12	37	12
12	13	38	13,2
13	13	39	12
14	13	40	7
15	19	41	13
16	13	42	11
17	13	43	11
18	13	44	10
19	12	45	9
20	13,2	46	10
21	12	47	12
22	7	48	13
23	13	49	13
24	11	50	13
25	11	51	19
26	10

---

Характеристики вариационного ряда:

• 
  максимальное значение ряда Х_max = 19;
  
• 
  минимальное значение ряда X_min = 7;
  
• 
  размах ряда определяется по формуле:
  

R = X_max – X_min = 19-7=12.

3.   1   2   3   4

---

Характеристики статистических рядов


Статистический ряд – перечень вариант и соответствующих им частот или относительных частот.

1. 
   Группированный статистический ряд
   

Группированный статистический ряд - ряд, в который, группируются значения с одинаковыми величинами.

Группированный статистический ряд для заданных исходных данных приведен в табл. 1.3.

Таблица 1.3 - Группированный статистический ряд

Хi	ni
7	3
9	3
10	6
11	6
12	9
13	18
13,2	3
19	3

Графическое представление статистических характеристик группированного ряда
Гистограмма для группированного ряда.

Гистограмма - представляет собой столбиковую диаграмму частот.

Гистограмма по заданным значениям группированного ряда показана на рисунке 1.2.



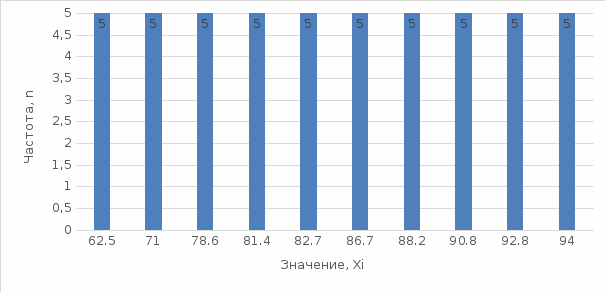
Рисунок 1.2 - Гистограмма для группированного ряда
Полигон для группированного ряда

Полигон – один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.

Полигон для группированного ряда показан на рисунке 1.3.



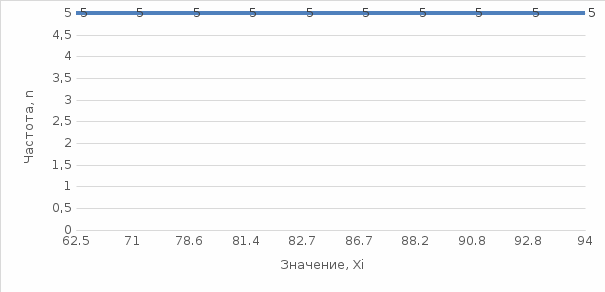
Рисунок 1.3 – Полигон для группированного ряда
Кумулята для группированного ряда.

Кумулята – один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и накопленных частот этих интервалов.

Кумулята для группированного показан на рисунке 1.4.

---

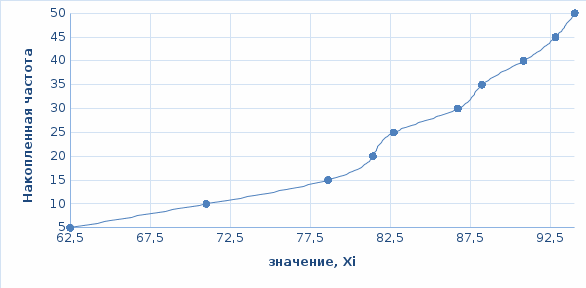
Рисунок 1.4 – Кумулята для группированного ряда
Огива для группированного ряда.

Огива – строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.

Огива для группированного ряда показана на рисунке 1.5.


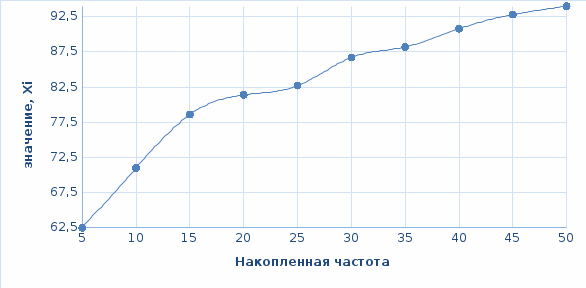
Рисунок 1.5 – Огива для группированного ряда
Статистические характеристики группированного ряда
Объем выборки группированного ряда.

Объем выборки – это количество элементов случайной величины, которые подлежат изучению.

Объём выборки определяется по формуле:
N= ,
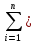где ni – частоты i-го интервала, а n – число значений в ряде.
При заданных значениях ряда получим:
N= 5+5+5+5+5+5+5+5+5+5=51.
Относительная частота.

Относительна частота - отношение частоты повторения конкретного значения случайной величины, относительно объема выборки.

Относительна частота определяется по формуле:
W = ni/n,
где ni – частота i-го интервала (всего 8); n – общий объем выборки.
Для первого значения ряда получим:
W = 3/51 = 0,059.
Значения относительных частот приведены в таблице 1.4.
Таблица 1.4- Относительные частоты для группированного ряда

Частота повторений	Сумма n	Относительная частота W	Сумма относительной частоты
3	51	0,059	1
3		0,059
6		0,118
6		0,118
9		0,176
18		0,353
3		0,059
3		0,059

Среднее арифметическое группированного ряда.

Среднее арифметическое ряда - разновидность среднего значения. Определяется как число

---