Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 233
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, равное сумме всех чисел группированного ряда, делённой на их количество (объем выборки).
Среднее арифметическое ряда определяется по формуле:
Xср=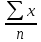 ,
,
где х – значение в группированном ряде (всего 51 значение)
n – количество значений (объем выборки)
Для заданных исходных данных получим:
Xср=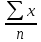 =
= 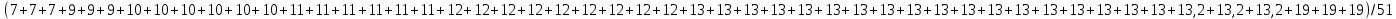 =12,01
=12,01
Средневзвешенное группированного ряда.
Средневзвешенное значение статистического ряда – разновидность среднего значения. Определяется как число, равное сумме произведений значений случайной величины и частоты ее повторения, делённой на сумму частот повторений.
Средневзвешенное значение статистического ряда определяется по формуле:
X=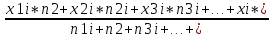 ,
,
где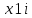 - значение варианта,
- значение варианта,
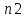 – частота повторения этого варианта в ряде от первого до i-го значения.
– частота повторения этого варианта в ряде от первого до i-го значения.
Для заданных исходных данных получим:
X=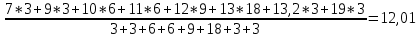
Мода группированного ряда
Мода – значение во множестве наблюдений, которое встречается наиболее часто.
Модой для группированного ряда будут является несколько значений с частотой равной четырем:
M = 13.
Медиана группированного ряда.
Медианой называется – элемент выборки, который делит пополам вариационный ряд на две части с одинаковым числом вариантов в каждой. Медиана (m0,5) – это значение СВ, которое делит вариационный ряд ограниченную кривой распределения, на две равные части.
Медиана для группированного ряда рассчитывается по формуле:
Me = (11+13)/2=12.
Дисперсия группированного ряда.
Дисперсия – это среднее арифметическое значение квадратов отклонений отдельных вариантов от их среднего арифметического.
Дисперсия может быть рассчитана по формуле:
D =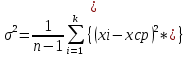 ,
,
где xi – i–й элемент группированного ряда;
xcp – среднее арифметическое значение
ni – частота повторения значения i-го значения в ряде.
n – число значений случайной величины (частота).
Данные для расчета дисперсии для других групп ряда приведены в таблице 1.5.
Таблица 1.5 – Данные для расчета дисперсии ряда
Тогда дисперсия для группированного ряда определится так:
D =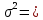 =(75,3003+27,1803+24,2406+6,1206+0,0009+17,6418+522,72+1083)/50= 1756,205/49 = 35,12.
=(75,3003+27,1803+24,2406+6,1206+0,0009+17,6418+522,72+1083)/50= 1756,205/49 = 35,12.
Среднее квадратическое отклонение группированного ряда.
Среднее квадратическое отклонение – это значение корня квадратного из дисперсии.
Среднее квадратическое отклонение рассчитывается по формуле:
σ =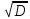 ,
,
где D – дисперсия группированного ряда
Для заданных исходных данных получим:
σ =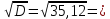 5,92
5,92
Коэффициент вариации группированного ряда
Коэффициент вариации – это величина, равная отношению среднеквадратичного отклонения случайной величины к среднему значению (среднему арифметическому) выраженная в процентах.
Коэффициент вариации определяется по формуле:
δ =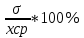
где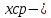
среднее арифметическое значение
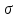 – среднее квадратичное.
– среднее квадратичное.
Для заданных исходных данных получим:
δ =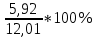 = 0,493%.
= 0,493%.
Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда, числовые значения которых приведены на рисунке 1.6.
Рисунок 1.6 – Характеристики описательной статистики
Вывод. Расчеты произведены вручную для группированного ряда сходятся с описательной статистикой, полученной в Exсel по исходным данным, но отличаются от данных рисунка 1.6 по причине не учитывания частот.
Интервальный ряд – ряд, группировка в котором выполняется по количеству попаданий в интервал.
Для построения интервального ряда примем количество интервалов t = 8.
Ширина интервалов определяется по формуле:
rt = R/t + Δt,
где - R – размах вариационного ряда;
t – количество интервалов
;
Δ – малая величина, позволяющая исключить повтор границ интервалов.
При заданных исходных данных получим:
rt = 12/8+0,0001=1,5
В таблице 1.6 показаны значения границ интервалов и средние значения величин каждого интервала.
Таблица 1.6 – Значения границ интервалов
Интервальный ряд представлен в таблице 1.7.
Таблица 1.7 - Интервальный ряд
Графическое представление статистических характеристик ряда
Гистограмма интервального ряда.
Гистограмма по средним значениям интервального ряда показана на рисунке 1.7.
Полигон интервального ряда.
Полигон для интервального ряда показан на рис. 1.8
Кумулята интервального ряда.
Кумулята для интервального ряда показан на рисунке 1.9.
Огива интервального ряда.
Огива для интервального ряда показана на рисунке 1.10.
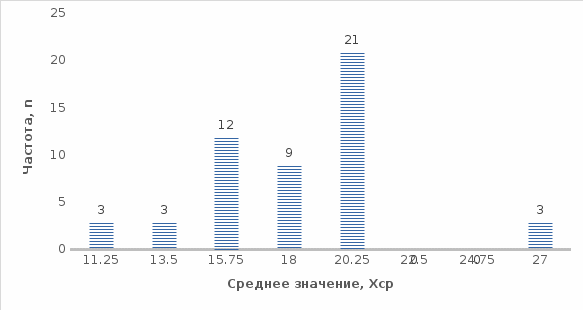
Рисунок 1.7 - Гистограмма для интервального ряда
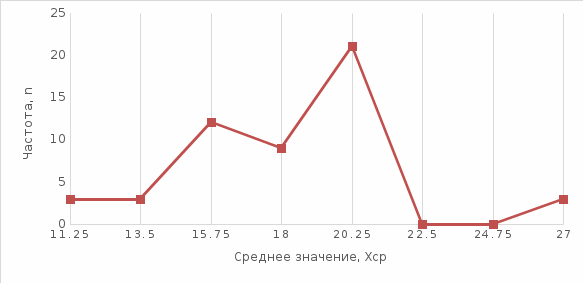
Рисунок 1.8 – Полигон для интервального ряда
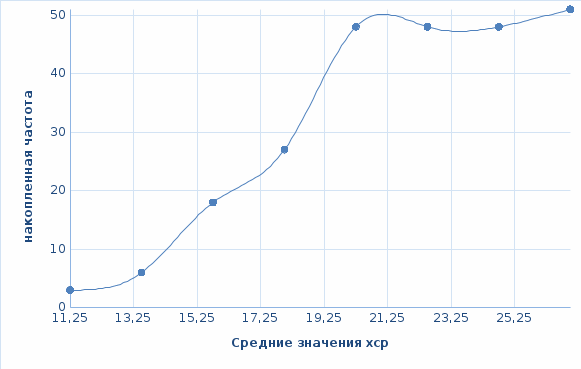
Рисунок 1.9 – Кумулята для группированного ряда
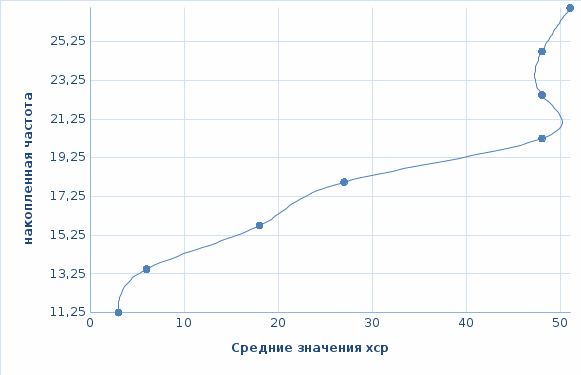
Рисунок 1.10 – Огива для интервального ряда
Статистические характеристики интервального ряда.
Объем выборки интервального ряда.
При заданных значениях интервального ряда получим объём выборки:
N= 3+3+12+9+21+0+0+3= 51
Относительная частота интервального ряда.
Для первого значения интервального ряда получим:
W = 3/51 = 0,058
Значения относительных частот приведены в таблице 1.8.
Таблица 1.8- Относительные частоты для группированного ряда
Среднее арифметическое интервального ряда.
Для заданных исходных данных получим:
Xср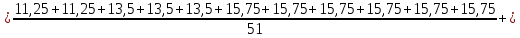
Среднее арифметическое ряда определяется по формуле:
Xср=
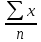 ,
,где х – значение в группированном ряде (всего 51 значение)
n – количество значений (объем выборки)
Для заданных исходных данных получим:
Xср=
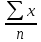 =
= 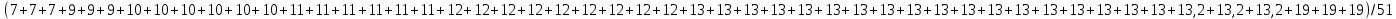 =12,01
=12,01Средневзвешенное группированного ряда.
Средневзвешенное значение статистического ряда – разновидность среднего значения. Определяется как число, равное сумме произведений значений случайной величины и частоты ее повторения, делённой на сумму частот повторений.
Средневзвешенное значение статистического ряда определяется по формуле:
X=
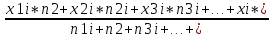 ,
,где
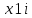 - значение варианта,
- значение варианта, 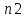 – частота повторения этого варианта в ряде от первого до i-го значения.
– частота повторения этого варианта в ряде от первого до i-го значения.Для заданных исходных данных получим:
X=
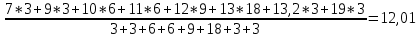
Мода группированного ряда
Мода – значение во множестве наблюдений, которое встречается наиболее часто.
Модой для группированного ряда будут является несколько значений с частотой равной четырем:
M = 13.
Медиана группированного ряда.
Медианой называется – элемент выборки, который делит пополам вариационный ряд на две части с одинаковым числом вариантов в каждой. Медиана (m0,5) – это значение СВ, которое делит вариационный ряд ограниченную кривой распределения, на две равные части.
Медиана для группированного ряда рассчитывается по формуле:
Me = (11+13)/2=12.
Дисперсия группированного ряда.
Дисперсия – это среднее арифметическое значение квадратов отклонений отдельных вариантов от их среднего арифметического.
Дисперсия может быть рассчитана по формуле:
D =
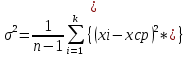 ,
,где xi – i–й элемент группированного ряда;
xcp – среднее арифметическое значение
ni – частота повторения значения i-го значения в ряде.
n – число значений случайной величины (частота).
Данные для расчета дисперсии для других групп ряда приведены в таблице 1.5.
Таблица 1.5 – Данные для расчета дисперсии ряда
| Номер группировки ряда | Значения СВ, Хi | Частоты ni | Среднее арифметическое | (xi-xср)2*nt | 1/(n-1) |
| 1 | 7 | 3 | 12,01 | 75,3003 | 1/50 |
| 2 | 9 | 3 | 27,1803 | ||
| 3 | 10 | 6 | 24,2406 | ||
| 4 | 11 | 6 | 6,1206 | ||
| 5 | 12 | 9 | 0,0009 | ||
| 6 | 13 | 18 | 17,6418 | ||
| 7 | 13,2 | 3 | 522,72 | ||
| 8 | 19 | 3 | 1083 |
Тогда дисперсия для группированного ряда определится так:
D =
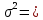 =(75,3003+27,1803+24,2406+6,1206+0,0009+17,6418+522,72+1083)/50= 1756,205/49 = 35,12.
=(75,3003+27,1803+24,2406+6,1206+0,0009+17,6418+522,72+1083)/50= 1756,205/49 = 35,12.Среднее квадратическое отклонение группированного ряда.
Среднее квадратическое отклонение – это значение корня квадратного из дисперсии.
Среднее квадратическое отклонение рассчитывается по формуле:
σ =
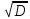 ,
,где D – дисперсия группированного ряда
Для заданных исходных данных получим:
σ =
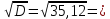 5,92
5,92Коэффициент вариации группированного ряда
Коэффициент вариации – это величина, равная отношению среднеквадратичного отклонения случайной величины к среднему значению (среднему арифметическому) выраженная в процентах.
Коэффициент вариации определяется по формуле:
δ =
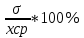
где
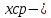
среднее арифметическое значение
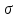 – среднее квадратичное.
– среднее квадратичное.Для заданных исходных данных получим:
δ =
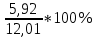 = 0,493%.
= 0,493%.Средствами программы Excel рассчитаны характеристики описательной статистики группированного ряда, числовые значения которых приведены на рисунке 1.6.
| Среднее | 11,775 |
| Стандартная ошибка | 1,267978 |
| Медиана | 11,5 |
| Мода | #Н/Д |
| Стандартное отклонение | 3,586383 |
| Дисперсия выборки | 12,86214 |
| Эксцесс | 1,982104 |
| Асимметричность | 1,014113 |
| Интервал | 12 |
| Минимум | 7 |
| Максимум | 19 |
| Сумма | 94,2 |
| Счет | 8 |
Рисунок 1.6 – Характеристики описательной статистики
Вывод. Расчеты произведены вручную для группированного ряда сходятся с описательной статистикой, полученной в Exсel по исходным данным, но отличаются от данных рисунка 1.6 по причине не учитывания частот.
-
Интервальный статистический ряд
Интервальный ряд – ряд, группировка в котором выполняется по количеству попаданий в интервал.
Для построения интервального ряда примем количество интервалов t = 8.
Ширина интервалов определяется по формуле:
rt = R/t + Δt,
где - R – размах вариационного ряда;
t – количество интервалов
;
Δ – малая величина, позволяющая исключить повтор границ интервалов.
При заданных исходных данных получим:
rt = 12/8+0,0001=1,5
В таблице 1.6 показаны значения границ интервалов и средние значения величин каждого интервала.
Таблица 1.6 – Значения границ интервалов
| Номер интервала, t | Значение левой границе интервала | Значение правой границе интервала | Среднее значение случайной величины в интервале |
| 1 | 7 | 8,5 | 11,25 |
| 2 | 8,5 | 10 | 13,5 |
| 3 | 10 | 11,5 | 15,75 |
| 4 | 11,5 | 13 | 18 |
| 5 | 13 | 14,5 | 20,25 |
| 6 | 14,5 | 16 | 22,5 |
| 7 | 16 | 17,5 | 24,75 |
| 8 | 17,5 | 19 | 27 |
Интервальный ряд представлен в таблице 1.7.
Таблица 1.7 - Интервальный ряд
| Номер интервала | Среднее значение xi | Частоты попадания в интервал | Накопленная частота |
| 1 | 11,25 | 3 | 3 |
| 2 | 13,5 | 3 | 6 |
| 3 | 15,75 | 12 | 18 |
| 4 | 18 | 9 | 27 |
| 5 | 20,25 | 21 | 48 |
| 6 | 22,5 | 0 | 0 |
| 7 | 24,75 | 0 | 0 |
| 8 | 27 | 3 | 51 |
Графическое представление статистических характеристик ряда
Гистограмма интервального ряда.
Гистограмма по средним значениям интервального ряда показана на рисунке 1.7.
Полигон интервального ряда.
Полигон для интервального ряда показан на рис. 1.8
Кумулята интервального ряда.
Кумулята для интервального ряда показан на рисунке 1.9.
Огива интервального ряда.
Огива для интервального ряда показана на рисунке 1.10.

Рисунок 1.7 - Гистограмма для интервального ряда

Рисунок 1.8 – Полигон для интервального ряда

Рисунок 1.9 – Кумулята для группированного ряда

Рисунок 1.10 – Огива для интервального ряда
Статистические характеристики интервального ряда.
Объем выборки интервального ряда.
При заданных значениях интервального ряда получим объём выборки:
N= 3+3+12+9+21+0+0+3= 51
Относительная частота интервального ряда.
Для первого значения интервального ряда получим:
W = 3/51 = 0,058
Значения относительных частот приведены в таблице 1.8.
Таблица 1.8- Относительные частоты для группированного ряда
| Частота | Сумма n | Относительная частота W | Сумма относительной частоты |
| 3 | 51 | 0,059 | 1 |
| 3 | 0,059 | ||
| 12 | 0,235 | ||
| 9 | 0,176 | ||
| 21 | 0,412 | ||
| 0 | 0 | ||
| 0 | 0 | ||
| 3 | 0,059 |
Среднее арифметическое интервального ряда.
Для заданных исходных данных получим:
Xср