Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx

Регрессионный анализ заданных последовательностей выполнен с помощью режима Регрессия пакета «Анализ данных» программы MS Excel. Сгенерируются результаты по регрессионной статистике, представленные в таблице 2.3.
Таблица 2.3- Результаты регрессионного анализа

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R			0,149781
R-квадрат			0,022434
Нормированный R-квадрат			0,002484
Стандартная ошибка			15,66512
Наблюдения			51
Дисперсионный анализ
	df			SS	MS			F			Значимость F
Регрессия	1			275,9503736	275,9503736			1,124510613			0,294148421
Остаток	49			12024,40257	245,3959708
Итого	50			12300,35294

---

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	73,08335	11,05977217	6,608034211	2,68632E-08	50,85790858	95,3088	50,85791	95,3088
Переменная X 1	-0,95699	0,902453475	-1,060429448	0,294148421	-2,770536395	0,85656	-2,77054	0,85656

Рассчитанные в таблицах характеристики представляют собой:

Множественный R — коэффициент корреляции R отражающий взаимосвязь двух и более случайных величин;

R-квадрат — коэффициент детерминации R ² — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными;

Нормированный R-квадрат – скорректированный R² с поправкой на число степеней свободы.

Стандартная ошибка — остаточное стандартное отклонение реальных значений от прогнозируемых.

Наблюдения — число наблюдений n.

df — число степеней свободы.

1. 
   Для строки Регрессиячисло степеней свободы определяется количеством факторных признаков m: k_ф=m=1.
   
2. 
   Для строки Остатокчисло степеней свободы определяется числом наблюдений nи количеством переменных в уравнении регресси: k_о = n - (m+1).
   
3. 
   Для строки - Итогочисло степеней свободы определяется суммой k_Y = k_Ф + k_о.
   

---

SS — сумма квадратов отклонений.

1. 
   Для строки Регрессия — это сумма квадратов отклонений теоретических данных от среднего:
   
2. 
   Для строки Остаток — это сумма квадратов отклонений эмпирических данных от теоретических:
   
3. 
   Для строки Итого — это сумма квадратов отклонений эмпирических данных от среднего.
   

MS— дисперсии:

1. 
   Для строки Регрессия — это факторная дисперсия.
   

2. 
   Для строки Остаток — это остаточная дисперсия. Остаточная дисперсия — это общая сумма квадратов отклонений расчетных значений от фактических (объем остаточной вариации), разделенная на число наблюдений.
   

F— расчетное значение F-критерия Фишера (вычисляемое по формуле).

Значимость F— значение уровня значимости, соответствующее вычисленному значению.

Коэффициенты — значения коэффициентов а_i.

Стандартная ошибка — стандартные ошибки коэффициентов a_i

t-статистика — расчетные значения t-критерия

Р-значение — значения уровней значимости, соответствующие вычисленным значениям t_p.

Нижние 95 % и Верхние 95 % — соответственно нижние и верхние границы доверительных интервалов для коэффициентов регрессии.
Построение регрессионных моделей выполнено с помощью команды «Построение линии тренда» программы Excel.

На нижеприведенных рисунках (рис. 2.2 - 2.6 показаны различные регрессионные модели, описывающие связь между двумя заданными последовательностями случайных величин.


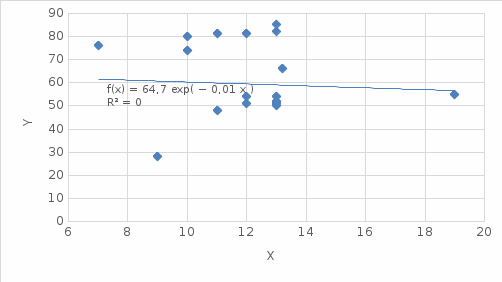
Рисунок 2.2 – Экспоненциальная модель


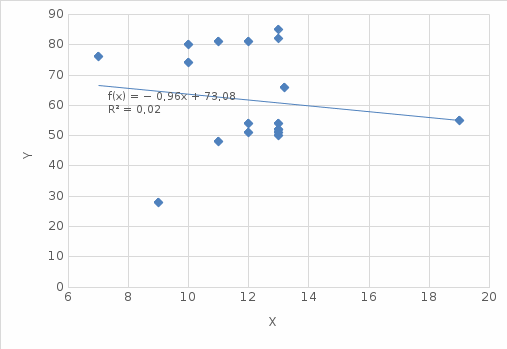
Рисунок 2.3 – Линейная модель


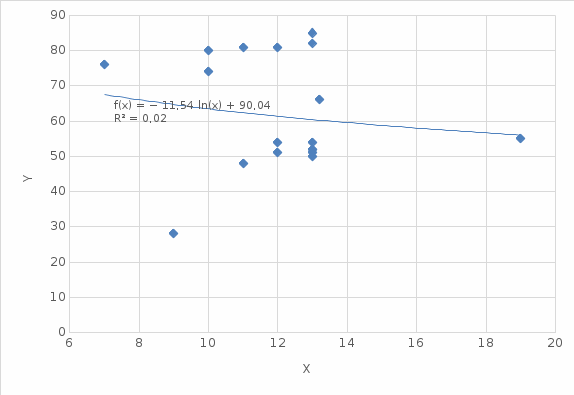
Рисунок 2.4 – Логарифмическая модель


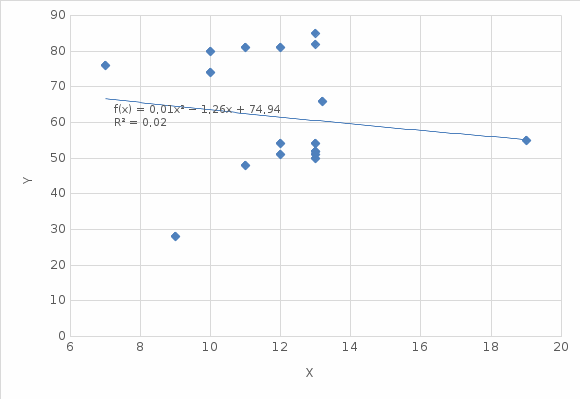
Рисунок 2.5 – Полиномиальная модель


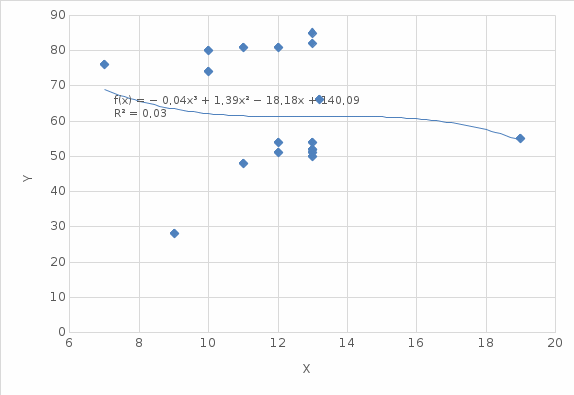
Рисунок 2.6 – Полиномиальная модель
В таблице 2.4 показаны сводные данные по всем построенным моделям.

Таблица 2.4 - Сводные данные построенных регрессионных моделей

№ п/п	Наименование модели	Вид уравнения	Величина достоверности детерминации, R2
1	Экспоненциальная	y=64,696e-0,007x	0,0039
2	Линейная	y = -0,957x + 73,083	0,0224
3	Логарифмическая	y = -11,54ln(x) + 90,043	0,023
4	Полиномиальная второй степени	y = 0,0116x2-1,2563x + 74,936	0,0225
5	Полиномиальная третьей степени	y = -0,0354x3 + 1,3925x2 - 18,178x + 140,09	0,0267

---

Вывод: Полиномиальная третьей степени модель обладает наибольшим значением величины достоверности детерминации 0,0267. Это означает что данная модель описывает все точки случайной величины наиболее точно и должна использоваться как модель.

---

Заключение

Мной были освоены компетенции выполнения статистического анализа двумерных данных, выявить практически отсутствующую зависимость между рассмотренными случайными величинами.

2. 
   ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
   

Реалистичное содержание целевой функции
В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов X_i) Y принят износ долота, мм.
Y = f(Х1, Х2, Х3).
Реалистичное содержание (сущность) факторов
В качестве факторов функции отклика X_i принимаются:
X₁ – количество оборотов ротора, об/мин;

X₂ – осевая нагрузка на долота, т;

Х₃ - плотность бурового раствора, кг/м³.
Уровни варьирования значений факторов
Минимальные и максимальные значения факторов приняты следующие:

Х1 min = 70 X1 max = 190

Х2 min= 10 X2 max= 20

Х3 min= 800 X3 max= 1500

Среднее значение фактора
Среднее значение фактора определяется по формуле:



Х₁₀=(190+70)/2=130 об/мин.

Х₂₀= (20+10)/2=15 тонн.

Х₃₀= (1500+800)/2=1150 кг/м³.

Интервалы варьирования фактора

Интервал варьирования определяется по формуле:

dx₁ = X₁₀ – X_1min = 130-70=60.

dx₂ = X₂₀ – X_2min = 15-10=5.

dx₃ = X₃₀ – X_3min = 1150-800=350.


Корректность определения значений факторов

Фактор	X1	X2	Х3
Минимальное значение, Хi min	70	10	800
Максимальное значение, Xi max	190	20	1500
Среднее значение, Xi 0	130	15	1150
Интервал варьирования dХi	60	5	350

---