Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 232
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Нормированные значения факторов
Нормированные значения определяются формулой:

Для заданных исходных данных:
Хн1 =
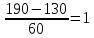 ;
;Хн2 =
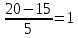 ;
;Хн3=
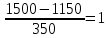 ;
;Матрица планирования полного факторного эксперимента
Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен, и равен 1.
| Номер опыта | Нулевой фактор | Нормированные факторы | Взаимодействия нормированных факторов | ||||||
| Х0н | Х1н | Х2н | Х3н | Х1н*Х2н | Х2нХ3н | Х1нХ3н | Х1нХ2нХ3н | ||
| 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | |
| 2 | 1 | 1 | -1 | -1 | -1 | 1 | -1 | 1 | |
| 3 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | |
| 4 | 1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | |
| 5 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | |
| 6 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | |
| 7 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
Экспериментальные значения целевой функции
| Номер опыта | Y1 | Y2 | Y3 | Y4 | Y5 |
| 1 | 4,759 | 4,709 | 4,745 | 4,768 | 4,05 |
| 2 | 4,828 | 4,801 | 4,845 | 4,845 | 4,45 |
| 3 | 4,243 | 4,253 | 4,242 | 4,3 | 4,85 |
| 4 | 5,612 | 5,613 | 5,563 | 5,598 | 5,25 |
| 5 | 5,612 | 5,613 | 5,563 | 5,598 | 5,65 |
| 6 | 6,612 | 6,613 | 6,563 | 6,598 | 6,05 |
| 7 | 7,759 | 7,709 | 7,745 | 7,768 | 7,85 |
| 8 | 7,828 | 7,801 | 7,845 | 7,845 | 7,55 |
Расчет среднего арифметического результатов каждого опыта
| Номер опыта | Y1 | Y2 | Y3 | Y4 | Y5 | Yср |
| 1 | 4,759 | 4,709 | 4,745 | 4,768 | 4,05 | 4,6062 |
| 2 | 4,828 | 4,801 | 4,845 | 4,845 | 4,45 | 4,7538 |
| 3 | 4,243 | 4,253 | 4,242 | 4,3 | 4,85 | 4,3776 |
| 4 | 5,612 | 5,613 | 5,563 | 5,598 | 5,25 | 5,5272 |
| 5 | 5,612 | 5,613 | 5,563 | 5,598 | 5,65 | 5,6072 |
| 6 | 6,612 | 6,613 | 6,563 | 6,598 | 6,05 | 6,4872 |
| 7 | 7,759 | 7,709 | 7,745 | 7,768 | 7,85 | 7,7662 |
| 8 | 7,828 | 7,801 | 7,845 | 7,845 | 7,55 | 7,7738 |
Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта)
Дисперсия среднего арифметического определяется формулой:
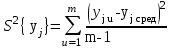
где m – количество параллельных опытов в строке матриц.
| Номер опыта | Y1 | Y2 | Y3 | Y4 | Y5 | Yср | S2y |
| 1 | 4,759 | 4,709 | 4,745 | 4,768 | 4,05 | 4,6062 | 0,0972 |
| 2 | 4,828 | 4,801 | 4,845 | 4,845 | 4,45 | 4,7538 | 0,0292 |
| 3 | 4,243 | 4,253 | 4,242 | 4,3 | 4,85 | 4,3776 | 0,0703 |
| 4 | 5,612 | 5,613 | 5,563 | 5,598 | 5,25 | 5,5272 | 0,0244 |
| 5 | 5,612 | 5,613 | 5,563 | 5,598 | 5,65 | 5,6072 | 0,0010 |
| 6 | 6,612 | 6,613 | 6,563 | 6,598 | 6,05 | 6,4872 | 0,0601 |
| 7 | 7,759 | 7,709 | 7,745 | 7,768 | 7,85 | 7,7662 | 0,0027 |
| 8 | 7,828 | 7,801 | 7,845 | 7,845 | 7,55 | 7,7738 | 0,0160 |
Расчетное значение критерия Кохрена
Критерий Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них, и определяется по формуле:

где S2max– наибольшая величина дисперсии результатов опыта;
si– дисперсия i-го опыта
N – общее число опытов в матрице.
Максимальное значение дисперсии результатов опыта:
S2ymax= 0,0972.
Сумма всех построчных дисперсий:
 S2 y = 0,0972+0,0292+0,0703+0,0244+0,0010+0,0601+0,0027+0,0160 = 0,30.
S2 y = 0,0972+0,0292+0,0703+0,0244+0,0010+0,0601+0,0027+0,0160 = 0,30.Расчетное значение критерия Кохрена:
Gp=
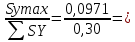 0,323.
0,323.В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N, где N – число опытов (количество строк в матрице планирования).
Табличное значение критерия Кохрена
Уровень значимости: = 0,05.
Степень числителя (f1): f1= m –1,
где m – количество параллельных опытов в строке матриц (5),
f1= 5 –1=4
Степень свободы знаменателя (f2):
f2 = N,
где N – общее число опытов в матрице.
f2 = 8,
Табличное значение критерия Кохрена
Gт = 0,391.
Вывод: Так как расчётное значение Gp, которое равно 0,323 меньше табличного значения Gт, которое равно 0,391, то соблюдается условие:
Gт > Gp ,
следовательно, с достоверностью 1 – , т.е. 0,95 все построчные дисперсии являются однородными. Исходные данные эксперимента могут считаться применимыми.
Вид уравнения регрессии, принятого для построения модели функции отклика
Рекомендуется полиномиальная модель функции отклика
y = b0+b1X1+ b2X2 + b3X3 + b12X1X2 + b23X2X3 + b31X3X1 + b123X1 X2 X3.
Коэффициенты регрессии.
Значения коэффициентов регрессии определяются по формулам:
 ;
; и так далее для всех коэффициентов.
Столбцы значений Х перемножается на столбцы Yср и делится на n и так далее для всех коэффициентов bi.
| Номер опыта | Нулевой фактор | Нормированные факторы | Взаимодействия нормированных факторов | Yср | ||||||
| Х0н | Х1н | Х2н | Х3н | Х1нХ2н | Х2нХ3н | Х1нХ3н | Х1нХ2нХ3н | |||
| 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 4,6062 | |
| 2 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 4,7538 | |
| 3 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 | 4,3776 | |
| 4 | 1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 5,5272 | |
| 5 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 5,6072 | |
| 6 | 1 | 1 | -1 | 1 | -1 | 1 | -1 | -1 | 6,4872 | |
| 7 | 1 | -1 | 1 | 1 | -1 | -1 | 1 | -1 | 7,7662 | |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 7,7738 | |
Таблица - Значения коэффициентов регрессии.
| b0 | b1 | b2 | b3 | b12 | b23 | b13 | b123 |
| 5,86 | 0,27 | 0,50 | 1,05 | 0,01 | -0,36 | -0,05 | 0,23 |
Статистическая значимость коэффициентов регрессии
Расчетные значения критерия Стьюдента
Оценка производится по t-критерию Стьюдента. Проверяется отклонение от нуля найденной оценки.
Для каждого коэффициента bk вычисляется расчетное значение критерия Стьюдента:
 ;
;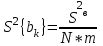 ;
;где bk – коэффициент уравнения регрессии;
S{bk} – оценку дисперсию коэффициентов, найденных по экспериментальным данным;
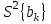 - дисперсия коэффициентов, найденных по экспериментальным данным;
- дисперсия коэффициентов, найденных по экспериментальным данным;S2в =
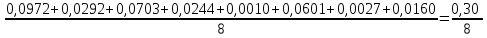 = 0,0376.
= 0,0376.S2{bk} =
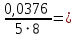 0,00094
0,00094S{bk} =
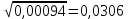 .
.Расчетные значения критерия Стьюдента
| t0 | t1 | t2 | t3 | t12 | t23 | t13 | t123 |
| 191,582 | 8,925 | 16,301 | 34,190 | 0,529 | 11,850 | 1,673 | 7,657 |