Файл: Методические указания по выполнению практических работ теория вероятностей и математическая статистика Специальность.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 1006
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2=0,4, р3=0,9 и р4=0,2. Найти математическое ожидание общего числа попадания.
Вариант 6. Производится 4 выстрела с вероятностью по падения в цель р1=0,3 р2=0,7, р3=0,3 и р4=0,5. Найти математическое ожидание общего числа попадания.
Задание №4.
Вариант 1. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.
Вариант 2. Вероятность отказа детали за время испытания на надежность равна 0,3. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 12 деталей.
Вариант 3. Вероятность отказа детали за время испытания на надежность равна 0,7. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 15 деталей.
Вариант 4. Вероятность отказа детали за время испытания на надежность равна 0,9. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 18 деталей.
Вариант 5. Вероятность отказа детали за время испытания на надежность равна 0,8. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 6 деталей.
Вариант 6. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 20деталей.
Задание №5
Вариант 1. Найти дисперсию случайной величины Х – числа появлений события в 100 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,7.
Вариант 2. Найти дисперсию случайной величины Х – числа появлений события в 130 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,6
Вариант 3. Найти дисперсию случайной величины Х – числа появлений события в 150 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,2.
Вариант 4. Найти дисперсию случайной величины Х – числа появлений события в 200 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,4.
Вариант 5. Найти дисперсию случайной величины Х – числа появлений события в 400 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,8.
Вариант 6. Найти дисперсию случайной величины Х – числа появлений события в 250 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,3.
Задание №6
Вариант 1. Случайная величина X может принимать два возможных значения х1 с вероятностью 0,3 и х2 с вероятностью 0,7, причем х2> x1. Найти х1 и х2, зная, что М (Х) = 2,7 и D (X) = 0,21.
Вариант 2. Случайная величина X может принимать два возможных значения х1 с вероятностью 0,4 и х2 с вероятностью 0,6, причем х1> x2. Найти х1 и х2, зная, что М (Х) = 3,4 и D (X) = 0,24.
Контрольные вопросы
ЛИТЕРАТУРА
Практическая работа №9
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ ДЛЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ; НАХОЖДЕНИЕ ФУНКЦИИ ПЛОТНОСТИ И ИНТЕГРАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Цель работы: научиться определять вероятности значений непрерывных случайных величин по функции распределения; научиться определять плотность распределения непрерывных случайных величин по функции распределения и наоборот.
Для выполнения работы необходимо знать виды случайных величин и их характеристики; необходимо уметь определять функцию распределения и плотность распределения непрерывных случайных величин.
Выполнение данной практической работы способствует формированию профессиональной компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x).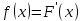
Пример 1. Дана функция распределения непрерывной случайной величины X. Найти плотность рапределения f(x).
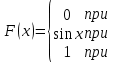
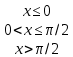
Решение. Плотность распределения равна первой производной от функции распределения:
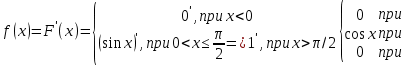
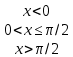
Вероятность того, что случайная величина примет значение, заключенное в интервале [а,b), можно найти, используя функцию распределения и плотность распределения.
При вычислении такой вероятности по функции распределения, используется формула P(a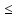 X<b)=F(b) - F(a).
X<b)=F(b) - F(a).
Пример 2. Случайная величина X задана функцией распределения
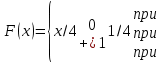
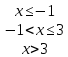
Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу [0,2):
Решение. Так как по условию (вторая строка) на интервале [0,2) F (x) = x/4+1/4, то
P (0X<2) = F (2) – F (0).
F(2) –F(0) = (2/4+1/4)-(0/4+1/4)=1/2.
Получим P (0X<2)=1/2.
Для нахождения вероятности попадания случайной величины в интервал по плотности распределения, используется формула P(a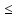 X<b)=
X<b)= 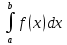
.
Пример 3. Задана плотность вероятности случайной величины X. Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу [0,5; 1).
f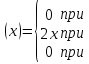
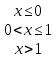
Решение. Искомая вероятность
P (0,5X<1)=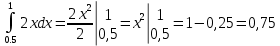
Зная плотность распределения можно найти функцию распределения по формуле:
F(x) =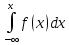
Пример 4. Случайная величина задана плотностью распределения. Найти: функцию распределения.
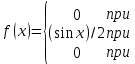
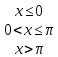
Решение
F(x) =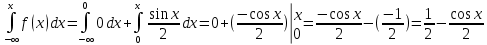
F(x) =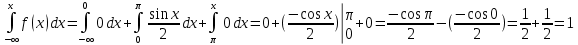 .
.
Ответ: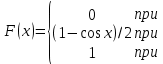
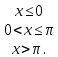
Пример 5. Плотность распределения непрерывной случайной величины X в интервале
(-π/2, π/2) равна f(x)=a*cos(x); вне этого интервала f(x)=0. Найти постоянный параметр a.
Решение.
Если функция f(x) представляет собой плотность распредеения вероятностей непрерывной случайной величины, заданной на интервале (a, b), то выполняется условие =1
=1
Найдем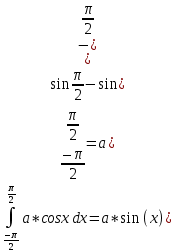
Приравнем результат к единице: 2a = 1. Таким образом, искомый параметр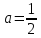 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
Вариант 6. Производится 4 выстрела с вероятностью по падения в цель р1=0,3 р2=0,7, р3=0,3 и р4=0,5. Найти математическое ожидание общего числа попадания.
Задание №4.
Вариант 1. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.
Вариант 2. Вероятность отказа детали за время испытания на надежность равна 0,3. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 12 деталей.
Вариант 3. Вероятность отказа детали за время испытания на надежность равна 0,7. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 15 деталей.
Вариант 4. Вероятность отказа детали за время испытания на надежность равна 0,9. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 18 деталей.
Вариант 5. Вероятность отказа детали за время испытания на надежность равна 0,8. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 6 деталей.
Вариант 6. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 20деталей.
Задание №5
Вариант 1. Найти дисперсию случайной величины Х – числа появлений события в 100 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,7.
Вариант 2. Найти дисперсию случайной величины Х – числа появлений события в 130 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,6
Вариант 3. Найти дисперсию случайной величины Х – числа появлений события в 150 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,2.
Вариант 4. Найти дисперсию случайной величины Х – числа появлений события в 200 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,4.
Вариант 5. Найти дисперсию случайной величины Х – числа появлений события в 400 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,8.
Вариант 6. Найти дисперсию случайной величины Х – числа появлений события в 250 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,3.
Задание №6
Вариант 1. Случайная величина X может принимать два возможных значения х1 с вероятностью 0,3 и х2 с вероятностью 0,7, причем х2> x1. Найти х1 и х2, зная, что М (Х) = 2,7 и D (X) = 0,21.
Вариант 2. Случайная величина X может принимать два возможных значения х1 с вероятностью 0,4 и х2 с вероятностью 0,6, причем х1> x2. Найти х1 и х2, зная, что М (Х) = 3,4 и D (X) = 0,24.
Контрольные вопросы
-
Дать определение математического ожидания -
Что показывает дисперсия случайной величины?
-
Как найти среднее квадратичное отклонение?
ЛИТЕРАТУРА
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007.
Практическая работа №9
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ ДЛЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ; НАХОЖДЕНИЕ ФУНКЦИИ ПЛОТНОСТИ И ИНТЕГРАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Цель работы: научиться определять вероятности значений непрерывных случайных величин по функции распределения; научиться определять плотность распределения непрерывных случайных величин по функции распределения и наоборот.
Для выполнения работы необходимо знать виды случайных величин и их характеристики; необходимо уметь определять функцию распределения и плотность распределения непрерывных случайных величин.
Выполнение данной практической работы способствует формированию профессиональной компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x).
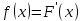
Пример 1. Дана функция распределения непрерывной случайной величины X. Найти плотность рапределения f(x).
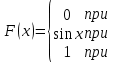
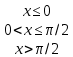
Решение. Плотность распределения равна первой производной от функции распределения:
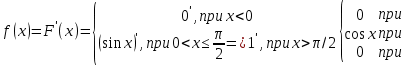
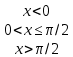
Вероятность того, что случайная величина примет значение, заключенное в интервале [а,b), можно найти, используя функцию распределения и плотность распределения.
При вычислении такой вероятности по функции распределения, используется формула P(a
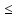 X<b)=F(b) - F(a).
X<b)=F(b) - F(a).Пример 2. Случайная величина X задана функцией распределения
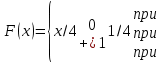
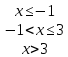
Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу [0,2):
Решение. Так как по условию (вторая строка) на интервале [0,2) F (x) = x/4+1/4, то
P (0X<2) = F (2) – F (0).
F(2) –F(0) = (2/4+1/4)-(0/4+1/4)=1/2.
Получим P (0X<2)=1/2.
Для нахождения вероятности попадания случайной величины в интервал по плотности распределения, используется формула P(a
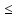 X<b)=
X<b)= 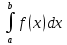
.
Пример 3. Задана плотность вероятности случайной величины X. Найти вероятность того, что в результате испытания X примет значение, принадлежащее интервалу [0,5; 1).
f
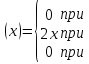
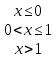
Решение. Искомая вероятность
P (0,5X<1)=
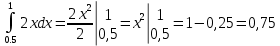
Зная плотность распределения можно найти функцию распределения по формуле:
F(x) =
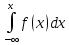
Пример 4. Случайная величина задана плотностью распределения. Найти: функцию распределения.
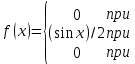
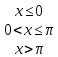
Решение
-
Если -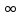
0, то F(x) = 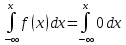 =0.
=0. -
Если 0,то
F(x) =
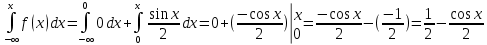
-
Если x>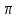
F(x) =
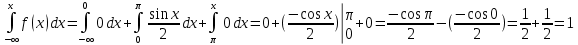 .
.Ответ:
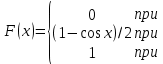
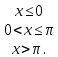
Пример 5. Плотность распределения непрерывной случайной величины X в интервале
(-π/2, π/2) равна f(x)=a*cos(x); вне этого интервала f(x)=0. Найти постоянный параметр a.
Решение.
Если функция f(x) представляет собой плотность распредеения вероятностей непрерывной случайной величины, заданной на интервале (a, b), то выполняется условие
 =1
=1Найдем
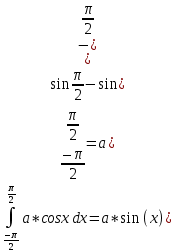
Приравнем результат к единице: 2a = 1. Таким образом, искомый параметр
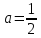 .
.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
| | I вариант | II вариант |
| 1. | Случайная величина X задана функцией распределения 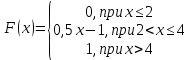 а) Найти плотность распределения f(x). б) Построить график функций F(x) и f(x) в) Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале [3 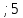 ) двумя способами: ) двумя способами:
| Случайная величина X задана функцией распределения 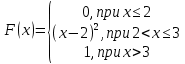 а) Найти плотность распределения f(x). б) Построить график функций F(x) и f(x) в) Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале [ 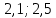 ) двумя способами: ) двумя способами:
|
| 2. | Дана функция распределения непрерывной случайной величины X 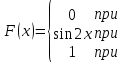 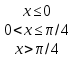 Найти плотность рапределения f(x). | Дана функция распределения непрерывной случайной величины X 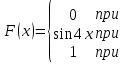 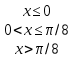 Найти плотность рапределения f(x). |
| 3. | Задана плотность распределения. Найти функцию распределения. 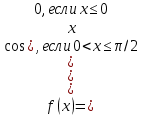 | Задана плотность распределения. Найти функцию распределения. 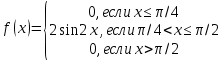 |
| 4. | Непрерывная случайная величина X задана плотностью распределения f(x)=(3/2)sin 3x в интервале (0, 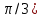 ; вне этого интервала f(x) = 0. Найти вероятность того, что X примет значение, принадлежащее интервалу ( ; вне этого интервала f(x) = 0. Найти вероятность того, что X примет значение, принадлежащее интервалу (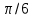 , ,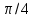 ). ). | Непрерывная случайная величина X задана плотностью распределения f(x)=(6/5)sin 3x в интервале (0, 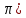 ; вне этого интервала f(x) = 0. Найти вероятность того, что X примет значение, принадлежащее интервалу ( ; вне этого интервала f(x) = 0. Найти вероятность того, что X примет значение, принадлежащее интервалу (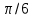 , ,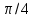 ). ). |
| 5*. | Плотность распределения непрерывной случайной величины X в интервале (0, π/3) равна f(x)=a*sin(3x); вне этого интервала f(x)=0. Найти постоянный параметр a. | Плотность распределения непрерывной случайной величины X в интервале (0, π/2) равна f(x)=a*sin(2x); вне этого интервала f(x)=0. Найти постоянный параметр a. |