Контрольные вопросы

1. 
   Какими формулами связаны функция распределения и плотность распределения непрерывной случайно величины?
   
2. 
   По каким формулам можно найти вероятность попадания непрерывной случайной величины в интервал [а,b)?
   

Таблица синусов и косинусов

Угол x	0		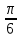		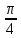	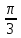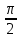π		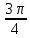2π
Sin(x)	0		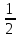		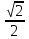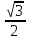1	0		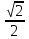0
Cos(x)	1		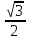		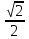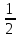0	-1		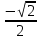1

Практическая работа №10

ВЫЧИСЛЕНИЕ ХАРАКТЕРИСТИК ДЛЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

С ПОМОЩЬЮ ФУНКЦИИ ПЛОТНОСТИ И ИНТЕГРАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Цель работы: научиться определять характеристики непрерывных случайных величин.

Для выполнения работы необходимо знать виды случайных величин и их характеристики; необходимо уметь определять числовые характеристики непрерывных случайных величин.

---

Выполнение данной практической работы способствует формированию профессиональной компетенций ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности, ПК 1.4. Принимать участие в приемо-сдаточных испытаниях, ПК 2.3. Применять методики тестирования разрабатываемых приложений.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут
КРАТКАЯ ТЕОРИЯ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Для непрерывной случайной величины можно определить следующие числовые характеристики:

• 
  Математическое ожидание – средневзвешенное по вероятностям значение случайной величины.
  

M(X) = 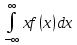- если возможные значения Х принадлежат всей числовой прямой.

• 
  Мода – наиболее вероятное значение случайной величины Х.
  
• 
  Дисперсия – характеризует разброс случайной величины вокруг ее математического ожидания.
  

D(X) = 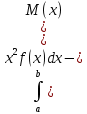- если возможные значения X принадлежат интервалу [a, b]

D(X) = M(x²)-(M(x))²

• 
  Среднее квадратичное отклонение - .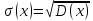
  

Рассмотрим примеры определения числовых характеристики непрерывных случайных величин.

Пример 1. Непрерывная случайная величина X задана плотностью распределения. Найти математическое ожидание.




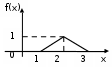
f(x) =

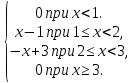
Решение

M(X) =
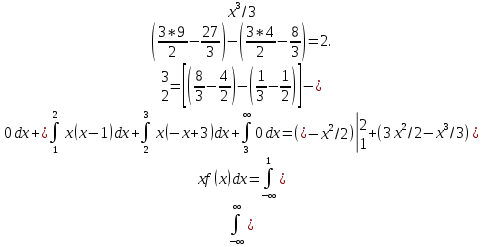
Пример 2. Случайная величина X задана плотностью распределения.

f(x) =

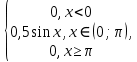
Найти математическое ожидание и моду.

Решение

1. 
   Математическое ожидание:
   

M(X) = 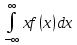= 0,5 .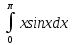

Для нахождения интеграла используем формулу интегрирование по частям.

---

U 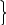= x dU = dx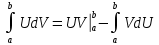

dV = sinxdx V = -cosx



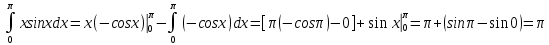
M(X) = 0,5 .

2. 
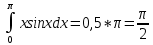   Мода:
   

(0,5sinx)’ = 0,5 cosx

0,5cos x = 0

cosx = 0 при x = + 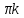– критические точки данной функции на всей числовой прямой

x = 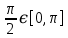– критическая точка в рассматриваемом интервале

x	0
y	0		0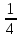

П роверим точку x = на максимум: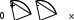



Т.к. в точке x = производная меняет знак с“+”на“-“, то в этой точке плотность вероятности будет максимальна.

Мода: m =
Пример 3. Случайная величина задана плотностью распределения:

f(x) = 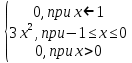Найти дисперсию и среднее квадратичное отклонение этой случайной величины.
Решение

1. Найдем математическое ожидание: M(X) = =

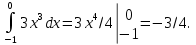
2. Определим дисперсию.

D(X) = =

---

3. 
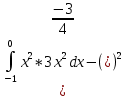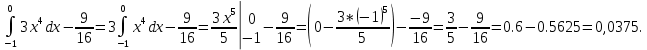
   Среднее квадратичное отклонение: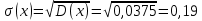
   

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ФОРМА ОТЧЕТНОСТИ
I вариант

1. 
   Случайная величина задана плотностью распределения:
   

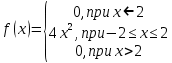
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение этой случайной величины

2. 
   Непрерывная случайная величина Х задана плотностью распределения
   

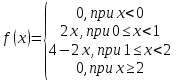
Найти математическое ожидание. Построить график f(x).

3. 
   Случайная величина задана функцией распределения:
   

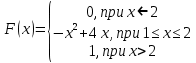
Найти моду этой случайной величины

4. 
   Случайная величина Х задана плотностью распределения:
   

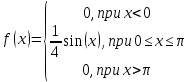
Найти математическое ожидание и моду.
II вариант

1. 
   Случайная величина задана плотностью распределения:
   

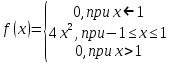
Найти дисперсию и среднеквадратичное отклонение этой случайной величины

2. 
   Непрерывная случайная величина Х задана плотностью распределения
   

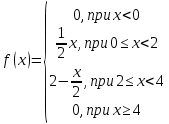Найти математическое ожидание. Построить график f(x).

3. 
   Случайная величина задана функцией распределения:
   

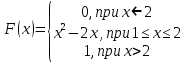
Найти моду этой случайной величины

4. 
   Случайная величина Х задана плотностью распределения:
   

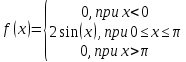Найти математическое ожидание и моду.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Чем отличаются формулы для нахождения математического ожидания дискретной и непрерывной случайных величин?
   
2. 
   Что характеризуется медиана непрерывной случайной велчины?
   

ЛИТЕРАТУРА

1. 
   Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2007. – 480 с.
   

Практическая работа №11

ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ ДЛЯ НОРМАЛЬНО, РАВНОМЕРНО И ПОКАЗАТЕЛЬНО РАСПРЕДЕЛЕННЫХ ВЕЛИЧИН

ЦЕЛЬ РАБОТЫ:

---

научиться вычислять вероятности для случайных величин, имеющих нормальное, равномерное и показательное распределения.
Для выполнения работы необходимо знать: виды случайных величин, их характеристики и распределения; необходимо уметь: определять вид распределения непрерывной случайной величины, вычислять вероятность попадания непрерывной случайной величины в определенный интервал.

Выполнение данной практической работы способствует формированию профессиональной компетенции ПК 1.2. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.
ВРЕМЯ ВЫПОЛНЕНИЯ: 90 минут.

---

Смотрите также файлы

• перпендикулярные прямые.docx

• Разработка урока в рамках формирования универсальных учебных действий (на примере темы Буквы Ш,ш, обозначающие согласный звук (ш, ) по учебному предмету русский язык (обучение грамоте).docx

• Добрый вечер, Алексей!.pdf

• Занятие для обучающихся 89 классов по теме день конституции.pdf

• Теоретические основы доступа информации как проблема региональной журналистики 5.doc