Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

При проектировании элементов конструкций стремятся сделать их во всех сечениях равнопрочными.

Рассмотренные три вида расчетов на прочность можно выполнять не только при растяжении или сжатии, а при любом виде деформации (сдвиге, кручении, изгибе).

При проектировании строительных конструкций расчет на прочность стальных элементов, подверженных центральному растяжению или сжатию, следует выполнять по формуле



где  – коэффициент условий работы, принимаемый по СНИП (см. табл. 3.1) или другим нормам.

 

Таблица 3.1

Элементы конструкции
Колонны общественных зданий и опор водонапорных башен Элементы стержневых конструкций покрытий и перекрытий: а) сжатых при расчетах на устойчивость б) растянутых в сварных конструкциях Сплошные составные балки, колонны, несущие статическую нагрузку и выполненные с помощью болтовых соединений, при расчетах на прочность Сечения прокатных и сварных элементов, несущих статическую нагрузку, при расчетах на прочность Сжатые элементы из одиночных уголков, прикрепляемые одной полкой	0,95   0,95 0,95   1,1   1,1 0,75
Примечание: В случаях, не оговоренных в настоящих нормах, в формулах следует принимать   .

                                             

 Для хрупких строительных материалов условия прочности принимают вид:

при растяжении:



при сжатии:



где   и   – допускаемые напряжения при растяжении и сжатии; n_t и n_c – нормативные коэффициенты запаса прочности по отношению к пределу прочности (n_t, n_c>1).

Для центрально сжатых бетонных элементов формула (2.33) записывается в виде:



где   – коэффициент, принимаемый для бетона тяжелого, мелкозернистого и легкого равным 1,00; для ячеистого автоклавного – 0,85; для ячеистого неавтоклавного – 0,75.

---

В некоторых случаях работоспособность элемента конструкции определяется не только его прочностью, но и жесткостью, т.е. способностью элемента воспринимать нагрузки без недопустимых упругих деформаций. При расчетах на жесткость определяют максимальные перемещения сечений и сопоставляют их с допускаемыми перемещениями.

Условие жесткости, ограничивающее изменение длины элемента, имеет сле­дующий общий вид:

где    - изменение размеров детали;

[ ] - допускаемая величина этого изме­нения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин    по участкам



условие жесткости при растяжении (сжатии) запишем следующим образом:



Так как перемещение, согласно закону Гука, зависит от нагрузки и размеров поперечного сечения, условие жесткости позволяет решать те же три вида задач, что и условие прочности.  

 

3.4. Расчеты статически определимых стержней
Статически определимый стержень – это стержень, который можно рассчитать, используя только уравнения равновесия (уравнения статики).

В любой науке, которая называется «точной» и в которой используются аналитические методы описания состояний и явлений, не обойтись без моделей. В нашем случае при решении различных задач мы каждый раз будем выбирать для рассматриваемого объекта расчетную схему.

Расчетная схема – это упрощенная схема конструкции или ее элементов, освобожденная от несущественных в данной задаче особенностей. При этом расчетная схема должна отражать все наиболее существенное для характера работы данной конструкции и не содержать второстепенных факторов, мало влияющих на результаты ее расчета. Построение и обоснование расчетной схемы – ответственный этап проектирования и расчета конструкции.

Перейдем к рассмотрению конкретных примеров.

 

Пример 5.

Чугунная труба-стойка высотой H=l=3м с наружным диаметром D=25 см и внутренним диаметром d=20 см нагружена сжимающей силой F=50 т, модуль упругости чугуна 

---

. Найти напряжение   в поперечном сечении колонны, абсолютное    и относительное укорочения  .

Решение.

Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной H=l=3м, жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 3.10, а.

Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая

продольная сила   



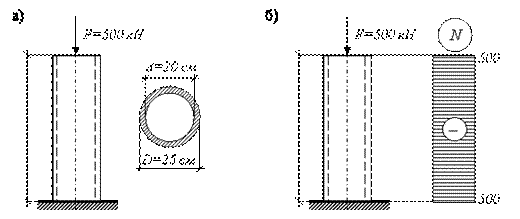
Рис. 3.10

 

Максимальное нормальное напряжение   определяется по формуле:



где A [м²]– площадь трубы:



тогда:



Абсолютное и относительное укорочения стойки определяем по формулам:





Знак "минус" обозначает уменьшение размера (укорочение).

3.5. Понятие о статически неопределимых системах

Основные положения. Связи необходимые и дополнительные.

Для решения задач сопротивления материалов необходимо знать все внешние силы, действующие на конструкцию, включая реакции наложенных на нее связей. Из теоретической механики известно, что для равновесия твердого тела, нагруженного плоской системой сил, достаточно наложить на тело три связи, а нагруженного пространственной системой сил – шесть связей. Соответственно для таких систем можно составить три и шесть независимых уравнений равновесия. Если при рассмотрении заданной системы, находящейся в рав­новесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления можно определить с помощью уравнений равновесия, без использо­вания дополнительных условий, то такая система называется 

---

ста­тически определимой.

В реальной практике встречаются такие конструкции, при рас­чете которых одних лишь уравнений равновесия оказывается не­достаточно, в связи с чем требуется формулирование дополнитель­ных уравнений, связанных с условиями деформирования конструк­ции.

Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.

В машиностроении и строительных конструкциях такие системы на­ходят широкое применение. В одних случаях статическая неопределимость является сущностью самой конструкции.

  

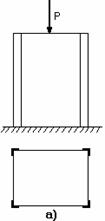
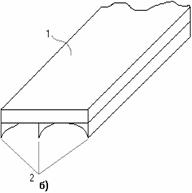
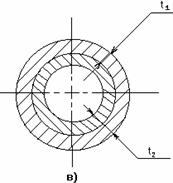
Рис. 3.11.

 

Примерами таких конструкций могут быть: армированные уголками стойки (рис.3.11, а); панель крыла самолета, состоящая из обшивки 1 с продольными ребрами 2 (рис. 3.11, б); составной цилиндр, полученный пу­тем напряженной посадки двух труб из различных материалов (рис. 3.11, в). В других случаях, с целью повышения жесткости и надежности сис­темы, вводятся дополнительные связи сверх тех минимально необходи­мых, которые обеспечивают ее кинематическую неизменяемость. Нало­жение на систему дополнительных связей превращает ее в статически неопределимую. Напомним, что кинематическая неизменяемость пло­ской системы обеспечивается тремя, а пространственной – шестью свя­зями.

Конструкции, состоящие из стержней, соединенных шарнирами, называются шарнирно-стержневыми. В этих конструкциях есть стержни, которые обеспечивают геометрическую неизменяемость конструкции и при удалении которых система превращается в механизм. Такие стержни будем называть необходимыми. Если же при удалении некоторых стержней геометрическая неизменяемость конструкции не нарушается, то такие стержни назовем лишними. Лишними такие связи называются только потому, что они не являются необходимыми для обеспечения равновесия конст­рукции и ее геометрической неизменяемости, хотя постановка их дикту­ется условиями эксплуатации. По условиям прочности и жесткости кон­струкции лишние связи могут оказаться необходимыми.

В статически определимой системе есть только необходимые стержни, в статически неопределимой – число лишних стержней равно степени статической неопределимости.

---

                                           

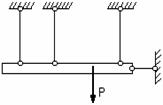
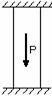
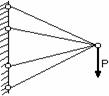
                             а)                                               б)                                        в)

Рис. 3.12

 

На рис. 3.12 приведены схемы 3-х плоских систем с «лишними» связями: а – стержневой подвески; б – стержня, закрепленного обоими концами; в – стержневого кронштейна. В схеме, показанной на рис. 3.12, в, вся система состоит из упругих звеньев. Подсчет числа наложенных связей произво­дится в этом случае следующим образом. Каждый стержень связан с опорной поверхностью двумя связями. Всего таких связей 8. Шарнир, соединяющий концы стержней, снимает связи, ограничивающие относи­тельный или взаимный их поворот. При соединении двух стержней од­ним шарниром снимается одна связь, трех стержней – две связи, четырех – три и т.д. В данном случае снимаются три связи. Следовательно, всех связей, наложенных на эту систему оказывается пять, две из которых мо­гут считаться «лишними».

Статически неопределимые конструкции характеризуются рядом осо­бенностей, по сравнению со статически определимыми системами. За­ключаются они в том, что в элементах статически неопределимых систем напряжения возникают не только от действия внешних сил, но и в ре­зультате изменения температуры, неточности изготовления деталей, не­точностей их сборки, смещения мест опорных креплений и ряда других причин. Объясняется это тем, что деформация одного из элементов в статически неопределимой системе приводит к деформа­ции и других ее элементов.

Например, если один из стержней системы (рис. 3.12, в) изготовлен по длине неточно, то соединение концов стержней одним шарниром возможно только путем деформации всех стержней.

Сила, возникающая при деформации одного из стержней, вызывает усилия в других стержнях, находящихся с ним в шарнирном соединении. Смонтированная система приходит в равновесие, следовательно, сово­купность сил системы обеспечивает ее равновесие. Эти силы вызывают соответствующие, называемые начальными, напряжения в стержнях.

---