Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

- Что называется жесткостью сечения при кручении?

- Что выражает условие жесткости при кручении?

- Чем объясняется, что вал кольцевого сечения при кручении экономичнее вала сплошного сечения?

- Как выполняют расчет вала на прочность?

- Как называется напряженное состояние, возникающее при кручении круглого бруса (вала)?

- Какие деформации возникают при кручении?

- Какие гипотезы выполняются при деформации кручения?

- По какой формуле определяется касательное напряжение при кручении?

- Как распределяется касательное напряжение при кручении? Чему равно напряжение в центре круглого поперечного сечения?

- Как вычислить потенциальную энергию деформации, накапливаемую валом при кручении?

- В каких точках бруса круглого сечения возникают наибольшее касательное напряжение? Как их вычисляют?

- Как определяется диаметр вала из условия жесткости?

- Как выбираются допускаемые напряжения при расчете на кручение?

- Укажите единицы измерения напряжений сдвига и смятия и модуля упругости.

- Что такое срез?

- Что такое смятие?

- Какие допущения проложены в основу практических расчетов элементов конструкции на срез и смятие?

- Опишите процесс разрушения при срезе?

- Как выбирается допускаемое напряжение при сдвиге?

- Что понимается под деформацией смятия?

- В чем заключается явление смятия и в каких местах оно наблюдается?

- Как записывается условие прочности на срез и на смятие?

- Как находится площадь смятия при соприкосновении цилиндрических поверхностей?

- Как определяется расчетная величина площади на срез и на смятие при болтовых соединениях листовых элементов внахлестку и с помощью накладок?

- Какие виды деформации испытывает нагруженное заклепочное соединение?

- Как учесть количество деталей, использованных для передачи нагрузки при расчетах на сдвиг и смятие?

- Как определить необходимое количество заклёпок, обеспечивающее безопасную прочность соединения?

6. Прямой изгиб

---

Общие сведения

Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.6.1, а). В этой же плоскости располагается изогнутая ось стержня (упругая линия) (рис.6.1, б). Брус, работающий при изгибе, называется балкой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).



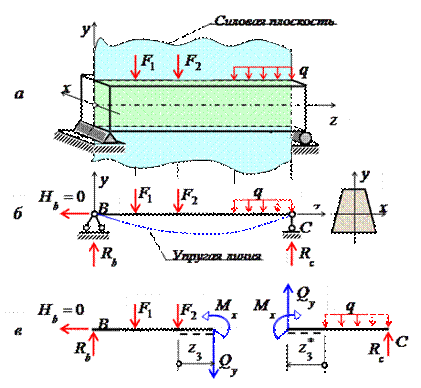
Рис. 6.1

При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.6.1,в): поперечная сила Q_y , где y – ось симметрии (главная центральная ось) и изгибающий момент M_x. , гдеx – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N,  поперечная Q силы и изгибающий момент M.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы Q_y изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; попереч­ный изгиб относят к простым видам сопротивления условно, так как в большинстве слу­чаев (для достаточно длинных балок) действием поперечной силы при расчетах на проч­ность можно пренебречь.

Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.

6.1. Построение эпюр поперечной силы и изгибающего момента
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.

Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.

---

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 6.2 показаны эти закрепления. Для неподвижной (рис 6.2,б) и подвижной (рис. 6.5,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.2,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 6.2,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.6.2,в).

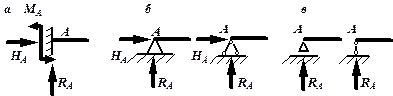
Рис. 6.2. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силуможно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.

---

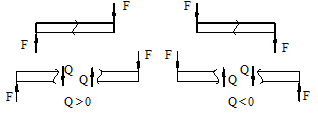
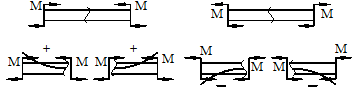
а)                                         б)
Рис.6.3. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

 

Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.4). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линией или осью.



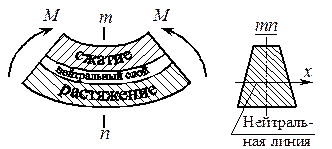
Рис.6.4
При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу Q_y и изгибающий момент M_x. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

На рис.6.5 показаны два случая оставшейся части: левая и правая.

Для определения величины Q_y и M_x составляются два уравнения равновесия для оставшейся части

---

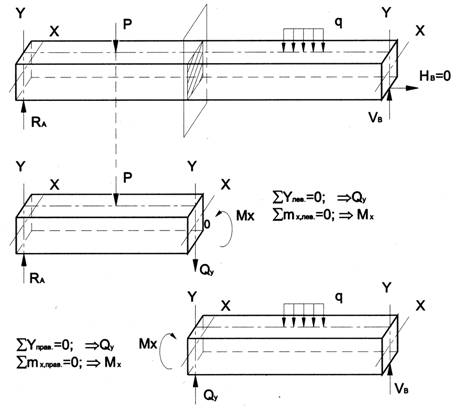
Рис.6.5
Изгибающий момент M_x, действующий в поперечном сечении балки, по величине равен сумме моментов всех внешних сил, приложенных к рассматриваемой отсеченной части бруса, относительно центральной оси x этого сечения:



Если внешняя сила в данном сечении растягивает нижние волокна балки, то момент этой силы в этом сечении считается положительным, если растягиваются верхние волокна балки, то момент этой силы будет отрицательным.

Поперечная сила Q_y в сечении бруса, по величине равна сумме проекций всех внешних сил, действующих на отсеченную часть бруса, на ось перпендикулярную оси бруса (ось y):



Уравнение момента составляется относительно оси Х, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила в уравнение не входит и величина M_x определяется независимо от Q_y. Можно доказать, что результат вычислений  Q_y и M_x не зависит от того, равновесие какой оставшейся части рассматривается.

Рассмотрим характерный пример (рис. 6.6,а) и установим не­обходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 6.6,б), выполняющими ту же роль, что и опорные закрепления.

Заданная система статически определима, следовательно, из ус­ловий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограниче­ний поворота сечений балки, поэтому изгибающих моментов не возникает)   и  , определяем вертикальные реакции в опорах:



Для определения   имеем:  откуда  . Для проверки правильности вычислений воспользуемся усло­вием равенства нулю суммы всех вертикальных сил   откуда получим

---