Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

Откуда



где    кривизна нейтрального волокна; EI_x  жесткость бруса.

Из формулы (3), исключая  , окончательно получим:



Эта формула была впервые получена Ш. Кулоном в 1773 году.

Таким образом, нормальные напряжения в любой точке сечения прямо пропорциональны величине изгибающего момента и расстоянию точки от нейтральной линии сечения и обратно пропорционально моменту инерции сечения относительно нейтральной оси.

Из выражения (5) можно сделать ряд важных выводов:

1) центр тяжести сечения балки является началом координат для анализа напряжений и приведения внешних сил;

2) напряжения изгиба зависят от значений изгибающего момента, момента инерции сечения и координаты точки, в которой это напряжение определяется;

3) напряжения в любой точке, лежащей на одинаковом расстоянии от нейтральной линии, равны между собой;

4) нормальные напряжения не зависят, а упругие перемещения зависят от модуля упругости материала балки.

В нейтральном слое при y=0 напряжения σ=0, в сжатой зоне (при y<0, рис.6.26) напряжения становятся отрицательными, в растянутой зоне (при y>0, рис. 6.26) напряжения становятся положительными. По мере удаления от нейтрального слоя нормальные напряжения σ в поперечном сече­нии бруса при его изгибе изменяются по линейному закону в зависимости от координаты y и принимают максимальное значение на уровне крайних волокон (при  ):





Измеряется осевой момент сопротивления единицами длины в третьей степени, например (см³). Физический смысл момента сопротивления состоит в следующем: чем больше W_x, тем больший изгибающий момент может принять на себя балка, не подвергаясь опасности разрушения. Таким образом, величина момента сопротивления характеризует влияние формы и размеров поперечного сечения балки на ее способность сопротивляться внешним нагрузкам, не разрушаясь

---

.

При симметричном относительно нейтральной линии сечении, например, прямоугольном, расстояния до крайних растянутых и сжатых волокон одинаковы и такое сечение имеет одно вполне определенное значение момента сопротивления относительно оси Oz. Так, при высоте прямоугольника (рис. 6.15, а), равной h





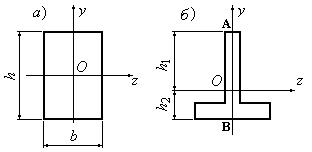
Рис. 6.15

 

Если сечение несимметрично относительно нейтральной линии – тавр, мы получим два момента сопротивления: один для волокон А (рис. 6.15,б):   и другой для волокон В:  . Теперь в формулу (6) следует вводить: W₁   при вычислении напряжений в точке А и W₂   при вычислении напряжений в точке В.

Для круга



Для прокатных профилей (двутавра, швеллера, уголка) M_x  приводится в таблицах сортамента.

Формулой (6) удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид



где maxM_x — максимальное значение изгибающего момента (легко определяемое по его эпюре), [σ] - допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором σ=const).
При расчете балок из хрупких материалов следует различать наибольшие растягивающие maxσ_pи наибольшие сжимающие maxσ_c напряжения, которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение [σ_p] и сжатие [σ_c]. Условие прочности в этом случае будет иметь вид:

---

В зависимости от того, чему лучше сопротивляется материал, приходится  соответсвующим образом конструировать сечение, выбирая его форму и размеры так, чтобы удовлетворяли условию прочности.

Из условия (7) формулируют три рода задач на прочность при изгибе:

1. Проверка прочности: задана балка, нагрузка, известен материал. Строится эпюра M_x  – определяется M_max, вычисляется W_x и по (7) проверяется условие прочности.

2. Определение максимально допустимой нагрузки по условию прочности.



Заданы размеры балки, характер нагрузки, материал балки.

Строится эпюра M_x  – определяется M_max от параметра нагрузки, вычисляется W_x и по (8) находят наибольший параметр нагрузки.

3. Конструирование балки – определение размеров ее поперечного сечения.



Строится эпюра   – определяется  , вычисляется правая часть (9) и подбираются размеры поперечного сечения, удовлетворяющие (9).

Для прямоугольного сечения 



Обычно задаются отношением



Тогда



отсюда 


Задаваясь шириной b по (10) получимh.

Для двутаврового сечения по таблице сортамента подбирают номер  двутавра  с  W_x  большим, чем правая часть (9).
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
- Что называется балкой?

- Какой вид нагружения называется изгибом?

- Какой изгиб называется чистым, поперечным?

- Какой изгиб называют чистым, поперечным, прямым и косым?

- Чем отличается чистый изгиб от поперечного изгиба, прямой изгиб от косого изгиба?

- Сформулируйте определение «поперечный изгиб»?

- Сформулируйте понятие «чистый изгиб»?

- Что понимается под волокнами бруса? В чем сущность гипотезы   плоских   сечений  и  допущения о ненадавливании волокон друг на друга?

---

- Что такое нейтральная линия, силовая линия?

- Какие внутренние усилия возникают в поперечных сечениях балки в общем случае действия на неё плоской системы сил?

- Как формулируется гипотеза плоских сечений?

- Что представляет собой нейтральный слой и нейтральная ось?

- Какие силовые факторы возникают в сечении балки при чистом изгибе?

- Какие силовые факторы возникают в сечении при поперечном изгибе?

- Что такое поперечная сила (Q_y)?   Как определяется Q_y  через внешние силы?

- Какие виды опор встречаются при расчете балок? Чем они отличаются?

- Какое правило законов для определения поперечной силы используется?

- Каково правило законов для определения изгибающего момента используется?

- Как вычисляется изгибающий момент в поперечном сечении балки?

- Как вычисляются поперечная и продольная силы в поперечном сечении балки?

- Как определить значение поперечной силы и изгибающего момента в произвольном сечении балки?

- Как определить знаки поперечной силы и изгибающего момента?

- Как проверить правильность определения опорных реакций?

- Как формулируется гипотеза плоских сечений?

- По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?

- Для чего строят эпюры внутренних силовых факторов?

- Какая нагрузка вызывает скачок на эпюре поперечной силы?

- Какая нагрузка вызывает скачок на эпюре изгибающего момента?

- Как находят опасные сечения?

- Какая дифференциальная зависимость связывает q, Q и M?

- Какие допущения положены в основу вывода формулы для определения нормальных напряжений при изгибе?

7. Сложное сопротивление

Основные сведения

При простых видах деформации (осевое растяжение или сжатие, сдвиг, кручение, плоский изгиб) в поперечных сечениях возникает только одно внутреннее усилие (продольная или поперечная сила, крутящий или изгибающий момент), за исключением плоского поперечного изгиба. На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более. Различные комбинации простых деформаций называются сложным сопротивлением.

В общем случае нагружения бруса в его поперечных сечениях действуют шесть компонентов внутренних усилий (

---

N, Q_x, Q_y, M_x, M_y, M_кр).



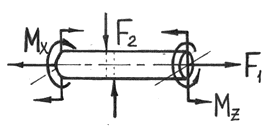
Рис. 7.1

Сложный вид деформации можно рассматривать как сумму простых видов, изученных ранее (растяжение, изгиб, кручение), при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор (рис.7.2): нормальная сила N - при растяжении, изгибающий момент

М_z - при чистом изгибе, крутящий момент М_x - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми.



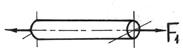
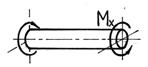
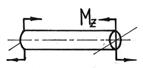
Рис.7.2

 

Основные соотношения, полученные для них, приведены в таблице 7.1

Таблица 7.1

Виды нагружения	Напряжения	Деформации
Растяжение	. Условие прочности:
Изгиб	Условие прочности:
Кручение	Условие прочности:

 

Но при сложном сопротивлении должен быть применим принцип независимости действия сил (частный случай принципа суперпозиции или наложения, применяемый в механике деформируемого твердого тела). 

Задачи на сложное сопротивление решаются следующим образом. Определяются напряжения и деформации при действии простейших видов деформации, составляющих сложное сопротивление, а затем полученные результаты суммируют, используя при необходимости теории прочности.

---