Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

0 = 0.



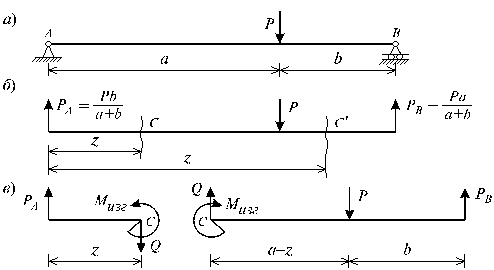
Рис. 6.6

               

Для определения внутренних силовых факторов  изгибающего момента М(z) и поперечной силы Q(z) как функций от продоль­ной координаты z, воспользуемся методом сечений. Для полу­чения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменя­ется жесткость балки; в точках, где происходит изменение ориен­тации элементов, если имеем дело с стержневой системой со сложной структурой.

Заданная система состоит из двух участков  первого (0≤z≤a) и второго (a≤z≤a+b). Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассмат­ривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних уси­лий, определим выражения для внутренних сило­вых факторов.

Из условия равновесия   отсеченной части системы, расположенной левее от сечения z₁ (первый участок), (см. рис. 6.6, в), получим:



Для определения Q_y и M_x на втором участке рассмотрим рав­новесие отсеченной части балки, расположенной правее от сечения z₂ (см. рис. 6.10, б), т.е.   откуда и определим:



Эпюры Q_y и M_x изображены на рис. 6.7. Заметим, что эпюры изгибающих моментов M_x, как и поперечных сил Q_y строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откла­дываются co стороны растянутых волокон.


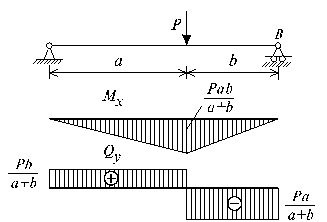
Рис. 6.7

---

 

6.2. Основные дифференциальные соотношения теории изгиба
Пусть брус нагружен произвольным образом распределенной нагрузкой q=f(z) (рис. 6.8,а).



Рис. 6.8

               

Выделим из бруса элемент длинойdz и приложим по его краям положительные внутренние усилия (рис. 6.8,б). В пределах малого отрезкаdz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, прохо­дящей через точку С (рис. 6.8,б), получим:





Производя упрощения и отбрасывая величины высшего поряд­ка малости, получим теорему Журавского (теорему Шведлера):



откуда



Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.

1. Эпюра Q является прямолинейной на всех участках. На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми (рис. 6.9).



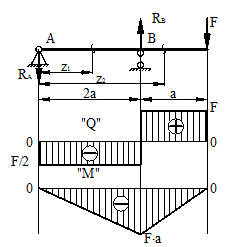
Рис.6.9

 

2. На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами (рис. 6.14). При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки (рис. 6.10,а, б).



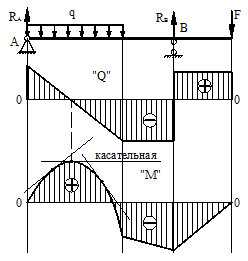
Рис.6.10

3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 6.10, 6.11). Изгибающий момент в таких сечениях балки экстремален по величине (М_max, M_min).

4. На участках, где 

---

Q>0, M возрастает, то есть слева на право положительные ординаты эпюры M монотонно увеличиваются, отрицательные – монотонно уменьшаются (рис. 6.9, 6.10); на тех участках, где Q < 0, M убывает (рис. 6.13, 6.14).

5. В тех сечениях, где к балке приложены сосредоточенные силы:

а) на эпюреQ будут скачки на величину и в направлении приложенных сил (рис. 6.13, 6.14).

б) на эпюре M будут переломы (рис. 6.9, 6.10), острие перелома направлено против действия силы.

6. В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюреQ никаких изменений не будет (рис. 6.12).



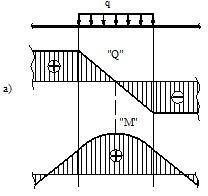
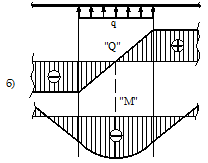
Рис.6.11

 



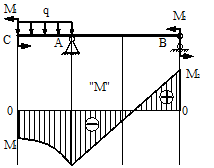
Рис.6.12

 

7. Если на конце консоли или в концевой опоре приложен сосредоточенный момент, то в этом сечении изгибающий момент равен внешнему моменту (сеченияC и B на рис. 6.12).

8. ЭпюраQ представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M (рис. 6.14).

9. Порядок линии на эпюре Q  всегда на единицу меньше, чем на эпюре M. Например, если эпюра M  - квадратная парабола, то эпюра Q  на этом участке - наклонная прямая; если эпюра M - наклонная прямая, то эпюра Q  на этом участке - прямая, параллельная оси; если M =const (прямая, параллельная оси), то на этом участке Q=0.

10. Приращение функции изгибающего момента на рассматриваемом участке численно равно площади эпюры поперечных сил на этом участке с соответствующим знаком. При построении эпюры  для изгибающего момента слева направо знаки приращения функции изгибающего момента и площади эпюры поперечных сил совпадают. При построении эпюры изгибающих моментов справа налево знаки приращения функции изгибающих моментов и площади эпюры поперечных сил противоположны. 

6.3. Напряжение при чистом изгибе

---

Рассмотрим наиболее простой случай изгиба, называемый чистым изгибом и выведем  формулу для определения нормальных напряжений для данного случая. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые гипотезы.

Таких гипотез при изгибе три:

1) гипотеза плоских сечений (гипотеза Бернулли). Сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной   осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.

Кроме этих гипотез следует ввести ряд ограничений:

1. Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости.

2. Материал балки подчиняется закону Гука, причем модуль упругости при растяжении и сжатии одинаков.

3. Соотношения между размерами балки таковы, что она работает в условиях плоского изгиба без коробления или скручивания.

Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а попе­речные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, вдоль продольной оси z принимает постоянное значение. Так как в любом сечении стержня при чистом изгибе M_x(z)=const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих мо­ментов ось бруса искривляется. Исходя из этого, ось бруса прини­мает форму дуги окружности с радиусом кривизны   (рис. 6.13). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба пере­местятся в пространстве таким образом, что их совокупность снова образует плоскость.

Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сече­ний друг относительно друга.

---

Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии  dz  (рис. 6.13).

В результате изгиба эти сечения наклонятся, образуя между со­бой угол dθ, в связи с чем верхние волокна удлиняются, а ниж­ние  укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом  . Произвольный отрезок АВ, расположен­ный от СD на расстоянии y, в результате изгиба удлинится на величину  . С учетом построений, изображенных на рис. 6.26, легко определить величину его относительной линейной деформации:



 

Рис. 6.13

 

Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения  сжатия. Тогда переход от деформаций к нормальным напряжениям   можно осуществить посредством закона Гука:



 


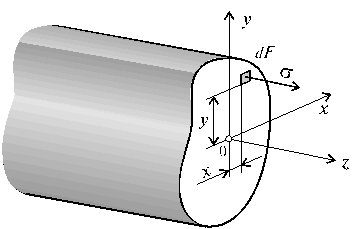
Рис. 6.14

               

Устано­вим положение нейт­ральной оси x, от кото­рой происходит отсчет координаты у (рис.6.14). Учитывая, что сумма элементарных сил   по площади попе­речного сечения A дает нормальную силу N_z. Но при чистом изгибе N_z =0, следовательно:



Как известно, последний интеграл представляет собой статиче­ский момент сечения относительно нейтральной линии (оси x). Статический момент равен нулю, значит, нейтральная линия про­ходит через центр тяжести сечения.

Выразим момент внутренних сил относительно нейтральной оси M_x  через σ. Очевидно, что



C учетом выражения (2) получим:

---