Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

9.3. Структура механизмов.
Понятие о структурном синтезе и анализе
Задачей структурного анализа является задача определения параметров структуры заданного механизма - числа звеньев и структурных групп, числа и вида КП, числа подвижностей (основных и местных), числа контуров и числа избыточных связей.

Задачей структурного синтеза является задача синтеза структуры нового механизма, обладающего заданными свойствами: числом подвижностей, отсутствием местных подвижностей и избыточных связей, минимумом числа звеньев, с парами определенного вида (например, только вращательными, как наиболее технологичными) и т.п.

Степень свободы и классы кинематических пар

Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой.

Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется  элементом кинематической пары.

Если звенья подвижно соединяются в нескольких местах, то кинематическая пара является разветвленной, а отдельные части этого соединения называются ветвями кинематической пары. 

Для абсолютно твердого тела, свободно движущегося в пространстве  пространстве (в декартовой системе координат X, Y, Z), число независимых параметров, определяющих его положение в пространстве или число степеней свободы, равно шести (рис.22): три возможных перемещения вдоль неподвижных координатных осей X, Y и Z и три возможных вращения вокруг этих осей.

 



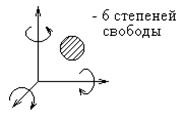
Рис. 9.22. Степени свободы тела в пространстве

 

Для звеньев, вошедших в кинематическую пару, число степеней свободы всегда меньше шести, так как кинематическая пара уменьшает число возможных перемещений и накладывает число условий связи S на относительное движение каждого звена, зависящих от способа соединения звеньев в пары. В таком случае число степеней свободы H  кинематической пары равно

H = 6 − S.                            (1)

---

Все кинематические пары делятся на классы в зависимости от числа условий связи, налагаемых ими на относительное движение звеньев. Так как число условий связи может быть от одного до пяти, то число классов пар равно пяти. В соответствии с этим имеем кинематические пары I −V классов. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. (рис. 9.22). При S=0 пары не существует, а есть два тела, движущихся независимо друг от друга. При S=6 кинематическая пара становится жестким соединением двух звеньев, т.е. одним звеном.

Класс кинематической пары может быть определен из зависимости (1):

S = 6 – H.                        (2)

 

Классификация кинематических пар
Кинематические пары (КП) классифицируются по следующим признакам:

1) по виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения). К низшим парам относятся: вращательная, поступательная, винтовая, цилиндрическая, сферическая, плоскостная и т.п. (Пример низшей кинематической пары: два цилиндра, находящиеся в постоянном соприкосновении, из которых один вращается внутри другого).

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). Они имеются, например, в зубчатых и кулачковых механизмах. При этом линейный или точечный контакт понимается как первоначальный - при соприкосновении звеньев без усилия, а под нагрузкой звенья, образующие высшую пару, будут соприкасаться по некоторой фактической поверхности, называемой пятном контакта.

 



Рис. 9.23
Преимуществом низших кинематических пар по сравнению с высшими является возможность передачи больших нагрузок, поскольку контактная поверхность соприкасающихся звеньев низшей пары может быть весьма значительной, имеют большие потери на трение, сложнее синтезируются. Имеют простые формы в виде плоскостей, цилиндрических поверхностей, поэтому более технологичны, т. е. просты в изготовлении.

---

 

Таблица 9.1. 

Условные обозначения кинематических пар

Класс пары	Число условий связи	Число степеней свободы	Название пары	Рисунок	Условное обозначение
I	1	5	Шар-плоскость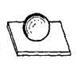
II	2	4	Шар-цилиндр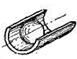
III	3	3	Сферическая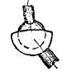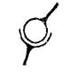
III	3	3	Плоскостная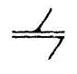
IV	4	2	Цилиндрическая
IV	4	2	Сферическая с пальцем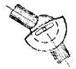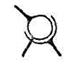
V	5	1	Поступательная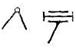
V	5	1	Вращательная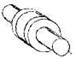
V	5	1	Винтовая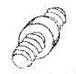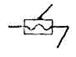

---

Кинематической цепью называется система звеньев, связанных между собой кинематическими парами.

Механизм − это кинематическая цепь, в которой при заданном движении одного или нескольких звеньев относительно одного из них все остальные звенья совершают однозначно определяемые движения.
Степень свободы и структурная формула механизма
Число степеней свободы механизма – это число степеней свободы всей кинематической цепи относительно неподвижного звена (стойки).

Если на движение звена в пространстве не наложено никаких условий связи, то оно обладает шестью степенями свободы. Тогда если число звеньев кинематической цепи равно к, то общее число степеней свободы, которым обладают к звеньев до их соединения в кинематические пары, равно 6к. Соединение звеньев в кинематические пары накладывает различное число условий связи S на относительное движение звеньев, зависящее от класса пар.

Если число пар I класса, у которого S₁=1, а H₁=5, в которые входят звенья рассматриваемой кинематической цепи, равно р₁, число пар II класса, у которого S₁=2, а H₁=4 – р₂, число пар III класса, у которого S₁=3, а H₁=3 – р₃, число пар IV класса, у которого S₁=4, а H₁=2 – р₄, число пар V класса, у которого S₁=5, а H₁=1 – р₅, то из 6к степеней свободы, которыми обладали звенья до вхождения в кинематические пары, необходимо исключить те степени свободы, которые отнимаются вхождением звеньев в кинематические пары. Тогда число степеней свободы Н кинематической цепи равно

Н = 6к - 5р₅ - 4р₄ - 3р₃ - 2р₂ – р₁.                           (3)

Формула (3) − это формула подвижности или структурная формула кинематической цепи общего вида. Данная формула называется формула Малышева, получена П.И. Сомовым в 1887 году и развита А.П. Малышевым в 1923 году.

Число степеней свободы W механизма относительно неподвижного звена будет равно

W = H – 6  или  W = 6(к-1) - 5p₅ - 4p₄ - 3p₃ - 2p₂ – p₁

или                 

W = 6n -5p₅ - 4p₄ - 3p₃ - 2

---

p₂ – p₁,                          (4)

где n=k-1 − число подвижных звеньев кинематической цепи. Формула (4) носит название формулы подвижности, или структурной формулы механизма общего вида.

Величина W показывает, сколько должно быть у механизма ведущих звеньев (если W = 1 – одно, W = 2 – два ведущих звена и т.д.).

Когда три связи уже наложены условием параллельности осей, структурная формула будет такой:

W = (6-3)n - (5-3)p₅ - (4-3)p₄ - (3-3)p₃,

или

W = 3n - 2p₅ – p₄.                           (5)

Формула (5) есть структурная формула для плоских механизмов общего вида. Формулу (5) называют также формулой П.Л. Чебышева (1869). Она может быть получена из формулы Малышева при условии, что на плоскости тело обладает не шестью, а тремя степенями свободы.

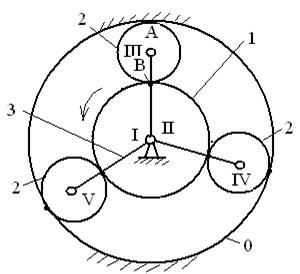
Показательным в этом отношении является пример зубчатого механизма планетарного типа, изображённый на рис. 9.24.

В состав механизма входит центральное колесо 1, являющееся ведущим, три параллельно работающих  сателлита 2 и стержневое звено 3, образующее вращательные пары с сателлитами. Все подвижные звенья размещены внутри неподвижного колеса 0 с внутренними зубьями. Данные для расчёта таковы: количество пар 5-го класса p₅=5 (они на схеме отмечены римскими цифрами), каждый  сателлит 2 образует зацепление (две кинематические пары) с колёсами 0 и 1, поэтому p₄=6, количество подвижных звеньев механизма n=5, количество степеней свободы механизма W=1.

1>

---