Файл: Методические рекомендации по суммативному оцениванию по предмету Алгебра и начала анализа.docx
Добавлен: 12.01.2024
Просмотров: 187
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Показательная и логарифмическая функции»








 Фамилия обучающегося
Фамилия обучающегося


 25
25
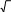
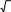
26
27
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Показательные и логарифмические уравнения и неравенства»





 Фамилия обучающегося
Фамилия обучающегося





 28
28








 Фамилия обучающегося
Фамилия обучающегося| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Строит график показательной функций | Затрудняется в построении графика показательной функции | Допускает ошибки при построении графиков показательной и логарифмической функций | Выполняет построение графиков показательной и логарифмической функций |
| Применяет свойства логарифмов при преобразовании логарифмических выражений | Затрудняется в применении свойств логарифмов при преобразовании логарифмических выражений | Допускает ошибки в применении свойств логарифмов при преобразовании логарифмических выражений | Находит числовое значение логарифмического выражения |
| Находит производные показательной и логарифмической функций | Затрудняется в нахождении производных показательной и логарифмической функций | Допускает ошибки в нахождении производных показательной и логарифмической функций | Находит производные показательной и логарифмической функций |
| Находит интеграл показательной функции | Затрудняется в нахождении интеграла показательной функции | Допускает ошибки в нахождении интеграла показательной функции | Находит интеграл показательной функции |


 25
25| Суммативное оценивание за раздел «Показательные и логарифмические уравнения и неравенства» | ||
| Тема | Показательные уравнения и их системы Логарифмические уравнения и их системы Показательные неравенства Логарифмические неравенства | |
| Цель обучения | 11.2.2.6 | Знать и применять методы решения |
| | | показательных уравнений |
| | 11.2.2.8 | Знать и применять методы решения |
| | | логарифмических уравнений |
| | 11.2.2.10 | Уметь решать показательные неравенства и |
| | | их системы |
| | 11.2.2.11 | Уметь решать логарифмические |
| | | неравенства и их системы |
| Критерий оценивания | Обучающийся
| |
| Уровень мыслительных навыков | Применение | |
| Время выполнения | 40 минут | |
| Задания
x 6x6 1
2 1
log 1 4x 7 log 1 x 1 2 2 log 2 x 2 log 2 x 2 log 2 5 | ||
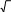
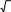
26
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Решает показательное уравнение | 1 | упрощает выражение, применяя свойства степени; | 1 |
| применяет метод решения однородного уравнения; | 1 | ||
| вводит новую переменную и приводит к квадратному уравнению; | 1 | ||
| находит корни квадратного уравнения; | 1 | ||
| возвращается к замене переменной и находит корни данного уравнения; | 1 | ||
| Решает логарифмическое уравнение | 2 | находит область допустимых значений; | 1 |
| приравнивает выражения, стоящие под знаком логарифма; | 1 | ||
| решает линейное уравнение и находит корень уравнения с учетом области допустимых значений; | 1 | ||
| Решает показательное неравенство | 3 | приводит неравенство к одному основанию; | 1 |
| решает дробно-рациональное неравенство; | 1 | ||
| применяет метод интервалов; | 1 | ||
| находит множество решений полученного неравенства; | 1 | ||
| Решает систему логарифмических неравенств | 4 | применяет свойства логарифмической функции; | 1 |
| составляет систему неравенств равносильную первому логарифмическому неравенству; | 1 | ||
| находит множество решений первого неравенства; | 1 | ||
| применяет свойство логарифма произведения; | 1 | ||
| составляет систему неравенств равносильную второму логарифмическому неравенству; | 1 | ||
| находит множество решений второго неравенства; | 1 | ||
| находит общее решение неравенств системы. | 1 | ||
| Итого: | 19 | ||
27
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Показательные и логарифмические уравнения и неравенства»





 Фамилия обучающегося
Фамилия обучающегося| Критерий оценивания | Уровень учебных достижений | ||
| Низкий | Средний | Высокий | |
| Решает показательное уравнение | Затрудняется в решении показательного уравнения | Допускает ошибки в решении показательного уравнения: в применении свойств степени; в арифметических вычислениях | Решает показательное уравнение, применяя метод введения новой переменной |
| Решает логарифмическое уравнение | Затрудняется в решении логарифмического уравнения | Допускает ошибки в решении логарифмического уравнения: в применении свойств логарифмов; в арифметических вычислениях | Применяет свойства логарифмов при решении логарифмического уравнения |
| Решает показательное неравенство | Затрудняется в решении показательного неравенства | Допускает ошибки в решении показательного неравенства: в применении свойств степени; в арифметических вычислениях | Решает показательное неравенство, применяя свойства показательной функции |
| Решает систему логарифмических неравенств | Затрудняется в решении системы логарифмических неравенств | Допускает ошибки в решении системы логарифмичеких неравенств; в нахождении общего решения | Решает систему логарифмических неравенств |





 28
28| ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ | ||
| Суммативное оценивание за раздел «Дифференциальные уравнения» | ||
| Тема | Основные сведения о дифференциальных уравнениях. Дифференциальные уравнения первого порядка c разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. | |
| Цель обучения | 11.4.1.23 | Знать определения частного и общего |
| | | решений дифференциального уравнения |
| | 11.4.1.24 | Решать дифференциальные уравнения с |
| | | разделяющимися переменными |
| | 11.4.3.1 | Применять дифференциальные уравнения при |
| | | решении физических задач |
| | 11.4.1.25 | Решать линейные однородные |
| | | дифференциальные уравнения второго |
| | | порядка (вида ay''+by'+cy=0 ,где a,b,c - |
| | | постоянные) |
| Критерий оценивания | Обучающийся
a,b,c - постоянные) | |
| Уровень мыслительных навыков | Применение Навыки высокого порядка | |
| Время выполнения | 40 минут | |
| Задания
Скорость изменения температуры воды в бутылке представлена дифференциальным уравнением: dТ 3 Т = . dt 125
Т Ae0,008t 3 , где А–произвольная постоянная. Учитывая, что температура воды в бутылке, когда она была помещена в холодильник, была 16 ° C,
y2
ex решение, удовлетворяющее начальному условию y(0) 2 .
| ||