Файл: ВсяМехЛАБраб2части.doc

Лабораторная работа № 1.3.

Определение коэффициента вязкости жидкости методом Стокса.

Цель работы: познакомиться с явлением внутреннего трения; изучить законы движения тел в вязкой жидкости; определить коэффициент вязкости касторового масла.

Приборы и принадлежности: стеклянный цилиндр на подставке с исследуемой жидкостью, металлические шарики разного материала и размеров, микрометр, секундомер, весы, миллиметровая линейка, термометр.

Краткая теория вопроса.

Пусть в покоящейся жидкости движется вверх перпендикулярно оси хпластинка со скоростью- средней скорости теплового движения молекул. Пластинка увлекает за собой прилегающий слой жидкости, который в свою очередь увлекает за собой следующий слой и т.д. Т.о., вся жидкость как бы делится на тончайшие слои, скользящие вверх тем медленнее, чем дальше они находятся от движущегося тела.

Очевидно, что при отсутствии взаимодействия между слоями жидкости и между жидкостью и пластинкой, каждый слой мог бы двигаться с произвольной скоростью, независимо от других. В действительности же распределение скоростей v(x)слоев газа от их расстояния до пластинки устанавливается в силу наличия вязкости, т.е. сил внутреннего трения в газе.

К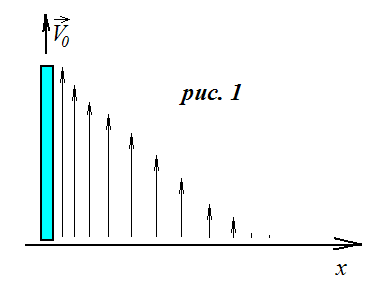аждая молекула жидкости принимает участие в 2 движениях: хаотичном (тепловом) и направленном (коллективном). Вектор средней скорости равен нулю в силу хаотичности его направленияуотдельных молекул, т.е. совокупность молекул, участвующих только в тепловом движении, в среднем будет оставаться на месте. При наличии же дополнительного направленного движения вся совокупность молекул в целом будет дрейфовать с постоянной скоростьюv.

Т.о. средний импульс отдельной молекулы в данном слое . Переходя из слоя в слой, молекулы переносят добавочное количество направленного движения, которое передается новому слою. Перемешивание молекул разных слоев (из-за хаотичности теплового движения) приводит к выравниванию скоростей переносного движенияvразных слоев, что и проявляется макроскопически как действие сил трения между слоями. Т.е.природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами: слои с более быстрыми молекулами передают некоторое количество движения медленному слою (ускоряют его), но теряя быстрые молекулы в обмен на более медленные сами при этом подвергаются торможению.

Так, сила трения между слоями соответствующими скоростям иравна:,

а сила трения, действующая на единицу площади границы соприкосновения соседних слоев:

- закон Ньютона.

Взаимодействие двух слоев можно рассматривать по закону Ньютона как процесс, при котором от одного слоя к другому передается в единицу времени импульс, по модулю равный действующей силе. Тогда можно записать: (1), где- плотность потока импульса – импульс, переносимый в ед. времени через ед. площадку (-ю осих) в положительном направлении осих.

- динамическая вязкость (коэффициент внутреннего трения) – выражается через силу трения между слоями, градиент скорости и площадь соприкосновения слоев: (2).Коэффициент динамической вязкости равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения слоев, движущихся один относительно другого с градиентом скорости, равным единице. Он зависит от природы жидкости и уменьшается с повышением ее температуры.

Закон (1) определяет и силу трения, возникающую на границе между жидкостью и движущимся в ней твердым телом. Можно показать, что сила сопротивления, испытываемая шаром, движущимся в вязкой жидкости, прямо пропорциональна вязкости жидкости , радиусу шараrи скорости его движения:

(3) - закон Стокса.

Эта формула выводится в предположении, что выполняются некоторые условия, в частности: 1) движение жидкости имеет ламинарный (слоистый) характер; 2) жидкость по всем направлениям простирается безгранично, т.е. в своих далеких точках остается в покое. Из первого условия следует, что скорость движения шарика должна быть невелика, из второго – размеры сосуда, в котором находится жидкость, должны быть весьма велики по сравнению с размерами шарика. Т.е. она применима в случае тел достаточно малых размеров и малых скоростей их движения. При больших скоростях вокруг движущихся тел возникают сложные вихревые движения жидкости, и сила сопротивления возрастает пропорционально квадрату скорости .

Описание метода Стокса.

Введем обозначения:

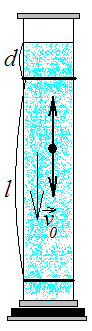
На движущийся в жидкости шарик действует сила внутреннего трения, тормозящая его движение. При условии, что стенки сосуда находятся далеко от шарика, эта сила по закону Стокса определяется формулой (3). Если шарик свободно падает в вязкой жидкости, то на него будут действовать также сила тяжести и выталкивающая сила Архимеда.

На основании 2-го закона динамики Ньютона имеем:

(4).

Решением полученного уравнения является закон изменения скорости шарика с течением времени при его падении в жидкости:

(5).

Поскольку с течением времени величина очень быстро убывает, то скорость шарика вначале возрастает (рис.2). Но через малый промежуток времени становится величиной постоянной, равной:(6), где.