ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1781
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
Р ис.
3.22. Пример графа для определения матрицS
и R
ис.
3.22. Пример графа для определения матрицS
и R
3.4. Операции над графами
3.4.1. Сумма графов
Пусть даны два графа G1(X) иG2(X) на одном и том же множестве вершин. ТогдасуммойграфовG1(X) иG2(X) является графG(X), состоящий из ребер, принадлежащихG1(X) илиG2(X).
Таким образом, если (хi', хj')G1(X) и (хi",хj")G2(X), то (хi', хj')G(X) и (хi", хj")G(X)(хi', хj', хi", хj")X.
Символически сумму двух графов обозначают следующим образом: G(X) =G1(X)G2(X). Аналогично определяется суммаnграфовGi(X) (i= 1, ...,n):
G(X)
=![]()
как граф, состоящий из ребер, принадлежащих хотя бы одному из графов Gi(X) (рис. 3.24).
Операция суммирования графов обладает переместительным свойством: G1(X)G2(X) =G2(X)G1(X).
Рассмотрим случай, когда операция суммы графов применяется к графам, определенным на различных множествах вершин. Тогда суммой G(X) будет граф
G(X) =
G1(X1)
G2(X2)
…
Gn (Xn)
=![]() ,
,
для которого справедливо:
X![]() = X1
X2
...
Xn
= X1
X2
...
Xn
и G(хj) = G1(хj) G2(xj) … Gn(хj) = , хjХ.
Сумма графов G1(X1) и G2(X2) изображена на рис. 3.23.
Пример 1

Рис. 3.23. Суммирование графов с различными множествами вершин
Пример 2


Рис. 3.24. Суммирование графов с одинаковыми множествами вершин
3.4.2. Пересечение графов
Пусть даны два графа G1(X) иG2(X) на одном и том же множестве вершин. ТогдапересечениемграфовG1(X) иG2(X) называется графG(X), состоящий из ребер, принадлежащих иG1(X) иG2(X), то есть если (хi, хj)G1(X) и (хi, хj)G2(X), то (хi, хj)G(X).
Обозначение пересечения двух графов:
G(X) =G1(X)G2(X).
Аналогично
пересечение nграфовGi(X)
(i= 1, ...,n)
обозначается какG(X)
=![]() и определяет графG(X),
состоящий из ребер, принадлежащих всем
графамGi(X).
и определяет графG(X),
состоящий из ребер, принадлежащих всем
графамGi(X).
Для графов примера 2 (рис. 3.24) имеем:
а) пересечение G1(X)G2(X) =(ноль-граф);
б) пересечение G1(X) G2(X) (рис. 3.25).
Д![]() ля
графов, определенных на различных
множествах вершин операция пересечения
определяется следующим образом:
ля
графов, определенных на различных
множествах вершин операция пересечения
определяется следующим образом:
G(X) = G1(X1) G2(X2) … Gn (Xn) =
где X
= X1
X2
...
Xn
=![]()
и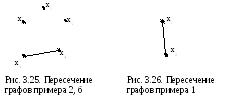 G(хj)
= G1(хj)
G2(хj)
…
Gn(хj)
=
G(хj)
= G1(хj)
G2(хj)
…
Gn(хj)
=![]() ,
хj
Х.
,
хj
Х.
3.5. Степени графов
3.5.1. Степени неориентированных графов
Пусть G(X) – неориентированный граф.Степеньюm(х)графаG(X) в вершине х называется число ребер, инцидентных вершине х. Если все числаm(х) для хXконечны, то граф называетсялокально конечным. Петли можно считать одинарным или двойным ребром в зависимости от конкретной задачи.
Обозначим m(хi, xj) =m(xj, хi) – число ребер, соединяющих вершины хiиxj. Если в графеG(X) нет кратных ребер, тоm(хi, xj) = 0 илиm(хi, xj) =l.
Очевидно, что
m(хi)
=![]()
Поскольку каждое ребро учитывается в двух вершинах хiиxj, то общее число реберmграфаG(X):
![]() . (7)
. (7)
Это выражение справедливо и для графов с петлями, если петлю считать двойным ребром.
Так как
![]() – четное число, то можно сделать вывод
о том, что в конечном графечисло вершин
с нечетной степенью четно. Это
следует из того, что если из суммы вычесть
все слагаемые, соответствующие вершинам
с четной степенью, она останется четной.
– четное число, то можно сделать вывод
о том, что в конечном графечисло вершин
с нечетной степенью четно. Это
следует из того, что если из суммы вычесть
все слагаемые, соответствующие вершинам
с четной степенью, она останется четной.
Граф, степени всех вершин в котором равны, называется однородным, т.е.m(xi) =mnxiX.
И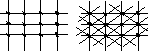 з
(7) следует, что в однородном графе степениmn,
число ребер равно
з
(7) следует, что в однородном графе степениmn,
число ребер равно
![]() гдеn- число вершин.
гдеn- число вершин.
Рис. 3.27. Бесконечные однородные графы
3.5.2. Степени ориентированных графов
В ориентированном графе существуют такие понятия, как полустепени исхода и захода.
Полустепенью исхода m'(х) называется число дуг, выходящих из вершины х. Полустепень захода m"(х) – число дуг, входящих в вершину х. Петли считают по одному разу в каждой из полустепеней.
Аналогом кратности неориентированных ребер m(xi,xj) в ориентированном графе являются две кратности:m'(xi, xj) – число дуг, направленных отxiкxj,m"(xi,xj) – число дуг, направленных отxjкxi.
Таким образом:
m'(xi, xj) = m"( xj, xi).
Число дуг, выходящих из вершины xi, определится суммой
![]()
а число дуг, входящих в вершину хi равно
![]()
Отсюда общее число дуг графа:
![]()
Если все полустепени m'(x) иm"(x) равны для всех хX, то ориентированный графG(X) называетсяоднородным графомстепениmn.
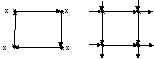
Рис. 3.28. Однородные ориентированные графы
Для такого графа m=mnхn, гдеnчисло вершин графаG(X). Примеры однородных ориентированных графов приведены на рис. 3.28.
3.6. Характеристики графов
3.6.1. Характеристики расстояний в графах
Пусть G(X) – конечный или бесконечный ориентированный граф.Отклонениемd(xi,xj) его вершиныxiот вершиныxjназывается длина кратчайшего пути из хiвxj:
d(xi,xj) =min{l[Sk(xi,xj)]}.
Отклонение d(xi,xj) удовлетворяет следующим аксиомам метрического пространства:
d(xi, xj) 0;
d(xi, xj) = 0 xi = xj;
d(xi, xj) + d(xj, xk) d(xi, xk) – неравенство треугольника и не удовлетворяет четвертой аксиоме, а именно:
d(xi, xj) d(xj, xi), так как граф ориентирован.
Необходимо отметить, что если xj G(xi), то d(xi, xj) = . Отклоненностью вершины xi называется наибольшее из отклонений d(xi, xj) по всем xj: