Файл: Diskretnaya_matematika.doc

Вычеркивая строки и столбцы, соответствующие обязательным импликантам х₁х₂х₄их₁х₂х₄, получим упрощенную импликантную таблицу (табл. 2.8).

Таблица 2.8. Упрощенная импликантная таблица

Из упрощенной таблицы видно, что простой импликант х₁х₃ х₄ покрывает обе оставшиеся конъюнкции. Теперь можно окончатель­но записать минимальную ДНФ для функцииf(х₁, х₂, х₃, х₄):

f(х₁, х₂, х₃, х₄) = х₁ х₂ х₄ х₁х₂х₄  х₁ х₃ х₄.

Для уменьшения количества проверок на возможность склеи­вания целесообразно все элементарные конъюнкции, содержащие одинаковое число букв, сгруппировать по признаку одинакового количества инвертированных (или не инвертированных) букв.

2.5. Синтез логических схем

С помощью аппарата логических функций можно получить наи­более компактное автоматное описание системы управления. Кроме того, этот аппарат может быть эффективно использован при перехо­де от автоматного описания к структурной реализации системы управления. Приведем одну из методик синтеза логической схемы с одним выходом, основанную на исходном представлении в виде совокупности таблиц истинности логических функций. Для пол­ноты изложения перечислим все этапы проектирования, хотя неко­торые из них уже были рассмотрены ранее.

Первый этап

1. По заданному в техническом задании алго­ритму выделяем независимые аргументы (входы) и выписываем все их комбинации (входные наборы). При большом количестве входов следует попытаться объединить их или реализовать устройство по частям.

2. Отмечаем запрещенные наборы, т.е. комбинации входных сигналов, которые не могут возникнуть.

3. Выписываем все значения выхода для каждого незапрещенного набора. При этом нужно проверить, зависит ли это значение только от комбинации входов, или еще и от последовательности их появления в каждой комбинации. В первом случае получим таблицу истинности. Во втором случае делаем вывод о том, что заданный алгоритм нельзя реализовать с помощью комбинационного устройства.

4. Доопределяем таблицу на запрещенных наборах, пользуясь информацией, имеющейся в алгоритме, либо руководствуясь сле­дующим (не всегда наилучшим) соображением: если в таблице больше единичных значений выхода, чем нулевых, она доопределя­ется единичными значениями и наоборот.

5. Записываем аналитическое выражение выхода как логической функции входов в СДНФ, если единичных значений выхода в таблице меньше, и в СКНФ – в противном случае.

Второй этап

6. Упрощаем полученное выражение. Для этой цели можно либо использовать известные методы минимизации логических функций, дающее минимально возможное в некотором смысле выражение, либо применить систему эквивалентных преоб­разований.

Эффект применения эквивалентных преобразований зависит от последовательности их применения. Наиболее важными являются склеивание х_i х_i = 1 и поглощение х_i  х_iх_j = х_i. К сожалению, нельзя указать такой порядок применения эквивалентных преобра­зований, который обеспечивал бы наиболее простую форму записи функции.

Третий этап

7. Пользуясь таблицами, имеющимися в литера­туре, преобразуем полученные на втором этапе выражения в такие, логические операции которых соответствуют выбранному функцио­нально полному набору элементов. При этом следует иметь в виду, что в новом базисе минимальность выражения не гарантируется.

8. Выбираем обозначение для каждой логической операции, реализуемой элементами данного набора. Существуют стандартные изображения базисных функций как некоторых блоков, техническая реализация которых может быть основана на использовании различ­ных физических явлений: магнитных, явлений в полупроводниках и т. д. Примеры таких символических обозначений представлены в таблице 2.9.

Т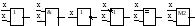аблица 2.9. Логические элементы и их обозначения

9. По аналитическому выражению строим логическую схему. При этом необходимо соблюдать очередность, раскрывая выраже­ние «изнутри наружу». Полученная в результате логическая схема может оказаться избыточной.

Пример. Пусть функция y = f(х₁, х₂, х₃, х₄) задана мини­мальной булевой формулой:

F = (х₁  х₂) х₃  (х₁  х₂) х₄.

При построении логической схемы по этой формуле потребуется шесть элементов, реализующих 6 операций. Но два из них реализуют одну и ту же функцию (х₁х₂). Поэтому можно упростить логическую схему, используя 5 логических элементов и задавая соответствующие связи между ними. Окончательно получим схему, изобра­женную на рис. 2.1.

Четвертый этап

10. От логической схемы выражения, описы­вающего работу системы управления, можно непосредственно пе­рейти к принципиальной схеме устройства, так как каждому услов­ному изображению функции на логической схеме соответствует физический элемент, реализующий данную операцию и имеющий не­сколько вариантов принципиальной схемы в зависимости от эле­ментной базы. Соединения между элементами задаются связями на логической схеме.

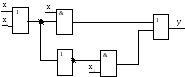
Рис. 2.1. Логическая схема

2.6. Контрольные вопросы и упражнения

1. Для высказывания А: «Любые два треугольника подоб­ны» сформулируйте отрицание и двойное отри­цание. Какие из этих трех высказываний истинны?

2. Даны высказывания: «Я купил велосипед» (А); «Я путешествовал по России» (В) и «Я участвовал в соревнованиях по велосипеду» (С). Сформулируйте высказывания, соответствующие формулам:

А В, А  В  С, А С, А  В, В С.

3. Даны высказывания:

«Четырехугольник MNPQ – парал­лело­грамм» (А);

«Диагонали четырехугольника MNPQ в точке пере­сечения делятся пополам» (В). Сформулируйте высказывания, соответ­ст­вующие формулам: А  В, В  А, А, В, А  В, В  А.

4. Составьте таблицы истинности для следующих формул:

F₁ = X  (Y  Z) и F₂ = (X Y)  (X  Z).

5. Покажите, что формулы являются тавтологиями:

F₁ = X   Y ~ Y  X;

F₂ = X   Y ~ Y  X;

F₃ = ((X  Y)  X)  Y.

6. Докажите равносильность формул:

а) F₁ = X  (Y  Z) и F₂ = (X  Y)  (X  Z);

б) F₁ = X  (Y  Z) и F₂ = (X  Y)  (X  Z);

в) F₁ = X  Y и F₂ =X Y;

г) F₁ = X  Y и F₂ =X Y;

д) F₁ = X  (Y  Z) и F₂ = (X  Y)  Z;

е) F₁ = (X  Y)  (X  Z) и F₂ = X  (Y  Z).

7. Постройте совершенные ДНФ и КНФ функций:

x₁ | x₂, x₁  x₂, x₁ ~ x₂.

8. Запишите СДНФ и СКНФ для логической функции f(x₁, х₂, х₃), принимающую значение 1 на наборах с номерами: 0, 3, 7. Определите, к каким классам функций относится эта функция.

9. Проверьте справедливость равенств:

а) х =х  1;

б) х₁  х₂ =х₁  x₂ .

10. Составьте таблицу свойств логической функции двух переменных. Из таблицы выпишите все полные системы булевых функций.

11. Проверьте линейность логической функции f(x₁, x₂, x₃), прини­мающей значение 1 на наборах с номерами: 0, 1, 5, 6.

12. Синтезируйте логические схемы функций из задач № 9, 12.

13. Найдите минимальную ДНФ функции f(х₁, х₂, х₃, х₄), прини­мающей значение 1 на наборах с номерами: 0, 1, 2, 5, 6, 7, 8, 12, 13.

14. Приведите примеры: