ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.08.2024
Просмотров: 1783
Скачиваний: 0
СОДЕРЖАНИЕ
1.4. Декартово произведение множеств
1.5.1. Определение бинарного отношения
1.5.2. Способы задания бинарного отношения
1.5.3. Свойства бинарных отношений
1.5.4. Отношения эквивалентности
1.7. Контрольные вопросы и упражнения
2.1.1. Логические высказывания
2.1.2. Основные логические операции
2.2.1. Булевы функции и операции
2.2.2. Совершенные дизъюнктивная и конъюнктивная нормальные формы
2.3. Полные системы логических функций
Класс функций, сохраняющих ноль
Класс функций, сохраняющих единицу
Класс самодвойственных функций
2.4.3. Минимизация днф методом Квайна
2.6. Контрольные вопросы и упражнения
3.1.2. Ориентированные и неориентированные графы
3.1.4. Частичные графы и подграфы
3.1.6. Изоморфизм. Плоские графы
3.2. Отношения на множествах и графы
3.3. Матрицы смежности и инциденций графа
3.5.1. Степени неориентированных графов
3.5.2. Степени ориентированных графов
3.6.1. Характеристики расстояний в графах
3.6.2. Характеристические числа графов
3.7.2 . Базисные циклы и разрезающие множества
Свойства базисных циклов и разрежающих множеств
3.7.3. Цикломатическая матрица и матрица разрезов
Составление цикломатической матрицы
3.8. Задача определения путей в графах
3.8.1. Определение путей в графе
3.8.2. Алгоритм определения кратчайших путей
а) монотонной функции, которая одновременно была бы линейной;
б) самодвойственной функции, которая одновременно была бы линейной;
в) линейной и монотонной функций.
Покажите, что функции Шеффера и Пирса не являются ни линейными, ни монотонными, ни самодвойственными.
Докажите полноту системы функций = {, ~ , 0}, состоящей из дизъюнкции, эквивалентности и константы 0.
3. Теория графов
На практике часто бывает полезно изобразить некоторую ситуацию в виде рисунков, составленных из точек (вершин), представляющих основные ситуации, и линий (ребер), соединяющих определенные пары этих вершин и представляющих связи между ними. Таким способом удобно представлять структуру системы, в которой вершины – это блоки, а ребра – связи между блоками. Такие рисунки известны под общим названием графов. Графы встречаются в разных областях под разными названиями: «структуры» в гражданском строительстве, «сети» в электротехнике, «социограммы» в социологии и экономике, «молекулярные структуры» в химии и т.д. Удобны графы и при исследовании систем методом пространства состояний. В этом случае вершины – состояния системы, процесса, ребра – действия, которые могут изменить состояние. При решении оптимизационных задач вершинами могут быть предполагаемые решения, ребрами – правила для их нахождения.
Начало теории графов как математической дисциплины было положено Эйлером в 1736 г., когда им была написана статья о Кенигсбергских мостах. Однако она была единственной в течение почти ста лет. Интерес к этой науке возродился около середины XIXв связи с развитием естественных наук (исследования электрических сетей, моделей кристаллов и структур молекул), формальной логики. Кроме того, оказалось, что многие математические головоломки могут быть сформулированы в терминах теории графов.
Последние 35-40 лет ознаменовали новый период интенсивных разработок теории графов. Появились новые области приложения: системы телекоммуникаций, биология, психология и другие.
3.1. Основные определения
3.1.1. Общие понятия
Граф Gзадается множествомвершин(точек) Х = {х1, ..., хn} и множествомребер(линий) А = {а1, .., аn}, соединяющих между собой все или часть этих вершин. Таким образом, графGполностью определяется заданием двух множеств (Х, А).
Другое часто употребляемое описание графа состоит в задании множества вершин Xи соответствия (отношения)G, которое показывает, как между собой связаны вершины. То есть граф задается следующим образом.
Пусть дано множество элементов X(вершин) графа и законG, позволяющий установить соответствие между каждым элементом х множестваXи некоторыми его подмножествамиG(x). Тогда граф полностью определяется множествомXи соответствиемG, то есть граф обозначается парой (X,G). Удобно использовать обозначениеG(X) по аналогии с функцией.
Пример.Для графа, изображенного на рис. 3.1: множество вершинX= {х0,х1,х2,х3,х4,х5} и закон соответствия между вершинами:
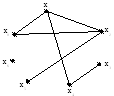
G(x 0) = {x1, x2},
G(x1) = {x0, x2, x4},
G(x2) = {x0, x1, x5},
G(x3) = {x4},
G(x4) = {x1, х3},
G(x5) = {x2},
G(x6) = .
Рис. 3.1. Пример задания графа
Ребра графа– линии, соединяющие вершины, указывают на соответствие между вершинами в графе.
Запись g= (xi,xj) говорит, что реброgинцидентновершинам хiиxj, а вершины хi,xjинцидентныребруg. Две вершины хi,xjназываютсясмежными, если они определяют ребро графа. Два ребра графа называютсясмежными, если их концы имеют общую вершину.
Вершина, не инцидентная никакому ребру графа, называется изолированной. Если граф состоит из изолированных вершин, его называютноль-графом.
3.1.2. Ориентированные и неориентированные графы
Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок) в графе не принимается во внимание.
Р ебро
графа называетсяориентированным,
если этот порядок существенен. В этом
случае говорят, что для ребраg= (xi,xj):xi–
начальная,axj– конечная вершины ребра.
ебро
графа называетсяориентированным,
если этот порядок существенен. В этом
случае говорят, что для ребраg= (xi,xj):xi–
начальная,axj– конечная вершины ребра.
Ориентированное ребро называют дугой графа (рис. 3.2).
Рис. 3.2. Дуга ориентированного графа
Граф называется неориентированным или неорграфом, если каждое ребро его не ориентированно, иориентированным или орграфом, если каждое ребро его ориентированно. Если граф содержит ориентированные и неориентированные ребра, он называетсясмешанным.
Полным неориентированным графомназывается графU(X), ребрами которого являются всевозможные пары (xi,xj) для всех возможных вершинxi,xjX,ij. В таком графе все вершины являются смежными (рис. 3.3).
Р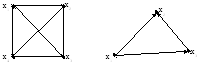 ис.
3.3. Полные неориентированный и
ис.
3.3. Полные неориентированный и
ориентированный графы
Полным ориентированным графом U0(X) называется граф, у которого любые две вершины соединены хотя бы в одном направлении.
П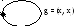 етлей
называется ребро g = (xi, xi),
у которого начальная и конечная вершины
совпадают (рис. 3.4) Петля обычно
считается неориентированной.
етлей
называется ребро g = (xi, xi),
у которого начальная и конечная вершины
совпадают (рис. 3.4) Петля обычно
считается неориентированной.
Рис. 3.4. Петля
Мультиграфомназывается граф, в котором пара вершин соединяется несколькими различными ребрами или дугами (рис.3.5).
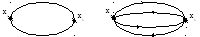
Рис. 3.5. Неориентированный и ориентированный мультиграфы
Дополнением графа G(X) является такой граф Gd(X), который совместно с графом G(X) образуют полный граф: U(X) = G(X) Gd(X).
3.1.3. Маршруты в графах
Маршрутомв произвольном графе называется чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной. В простом графе маршрут однозначно определяется только последовательностью вершин. Будем рассматривать следующие конечные маршруты, которые часто используются в задачах обхода графа: цепи, циклы и пути.
Для неориентированных графов справедливы следующие понятия.
Цепь– последовательность реберS= (g1,g2, ...,gn), в которой у каждого ребраgkодна из вершин является вершиной ребраgk-1, а другая - вершиной ребраgk+1. При этом одно и то же ребро или вершина может встречаться несколько раз. Пример цепи для графа (рис. 3.6):
S = (g0, gl, g2, g3, g4, g5, g2, gб) = ((x0, х1), (х1, х2), (х2, х3), (х3, х1), (х1, х4), (х4, х3), (х3, х2), (х2, х5)).
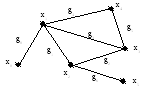
Рис. 3.6. Пример цепи
Цепь называется простой, если все ребра в ней различны, исложной (составной)– в противном случае. Вершины в простой цепи могут повторяться.
Цепь называется элементарной, если в ней ни одна из вершин не повторяется.
Циклом называется конечная цепь, начинающаяся на некоторой вершине хi, и окачивающаяся на ней же. Простые, сложные и элементарные циклы определяются по аналогии с цепями.
Для ориентированных графоввведены следующие дополнительные понятия.
Путемв графеG(X) называется такая последовательность дуг (gl,g2, …), что конец каждой предыдущей дуги является началом следующей. Существуют простые, сложные и элементарные пути.
Х|
Х0
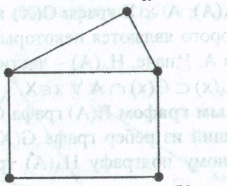
Длина пути есть число дуг L(s) в последовательности дуг пути s. В случае бесконечного пути L(s) = .
Г раф
называетсясимметрическим,еслиxi,xj
из того, чтоxiG(xj)xjG(xi),
то есть две смежные вершиныxi,xjвсегда соединены противоположно
ориентированными дугами (рис.3.7).
раф
называетсясимметрическим,еслиxi,xj
из того, чтоxiG(xj)xjG(xi),
то есть две смежные вершиныxi,xjвсегда соединены противоположно
ориентированными дугами (рис.3.7).
Рис. 3.7. Симметрический граф
Граф называется антисимметрическим, еслиxi,xj xiG(xj)xjG(xi), то есть каждая пара смежных вершин соединена только в одном направлении.
Граф называется конечным, если число его вершин конечно ибесконечным,если число вершин бесконечно. ГрафG(X) называетсяG – конечным, если для каждой его вершины хXмножествоG(x) конечно.
3.1.4. Частичные графы и подграфы
Граф Н(х) называется частичным для графа G(X), если все ребра Н(Х) являются ребрами G(X) и множество вершин графа Н(Х) совпадает с множеством вершин графа G(X), то есть Н(х) G(x) х X (рис.3.8).
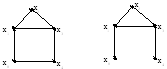
Рис. 3.8. Граф G(X) и частичный для него граф Н(Х)
Частичный граф содержит часть ребер(дуг). Он также может быть ориентированным или неориентированным в зависимости от исходного графа.
Отметим, что ноль-граф графа G(X) считается его частичным графом. Все частичные графы Н(Х) дляG(X) можно получить, выбирая в качестве ребер Н(Х) всевозможные подмножества множества ребер графаG(X).
ПодграфомGA(A) графаG(X), где АX, называется граф, вершинами которого являются элементы множества АX, а ребрами – все ребра изG, концевые вершины которых лежат в А (рис.3.9).
Хо
Хо
Х4
Р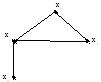 ис.
3.9. ПодграфGA(A)
графа G(X)
ис.
3.9. ПодграфGA(A)
графа G(X)
Таким образом, подграф содержит часть вершинвместе с ребрами, соединяющими эти вершины. Иначе,GA(A) – подграф графаG(X), если АXиGA(x) =G(x)Ах Х.
Если А = X, тоGA(A) =G(X). Для единственной вершины А = {а} подграфGA(a) состоит из петель вокруг а. ПодграфомGA(A) графаG(X) будет ноль-граф, если АXесть подмножество изолированных вершин графа.
П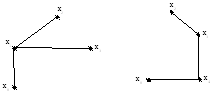 одграф
будет ориентированным или неориентированным
в зависимости от исходного графа.
одграф
будет ориентированным или неориентированным
в зависимости от исходного графа.
Рис. 3.10. Частичный
подграф НА(А)
графа G(X)
Рис. 3.11. Дополнительный
частичный граф Н(А) графа G(X)
Частичным подграфом НА(А), А X графа G(X) называется подграф (рис. 3.10), ребрами которого являются некоторые ребра из G(X), оба конца которых лежат в А. Иначе, НА(А) – частичный подграф графа G(X), если А X и НА(х) G(x) A х Х.