Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

Поскольку

,

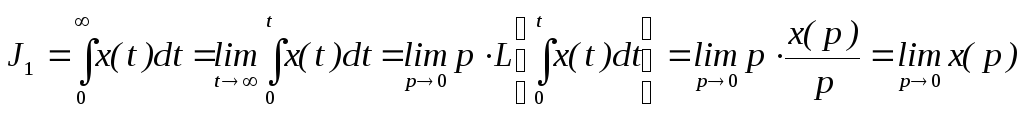и учитывая, что

= ,

(где - передаточная функция замкнутой системы), получаем выражение для расчета величины линейной интегральной оценкой качестваJ₁ по передаточной функции системы:

. (4.3)

Так, например, для системы с передаточной функцией

интегральная оценка J₁ , согласно выражению (4.3), равна:

.

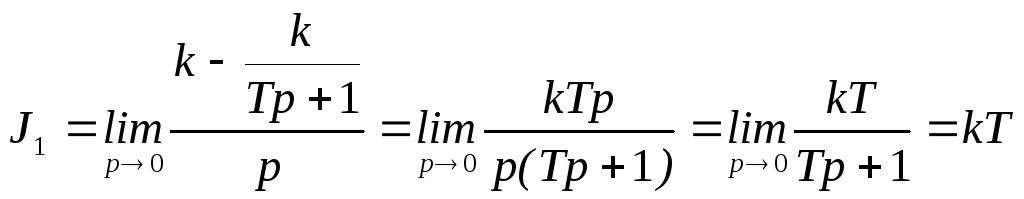Для системы с передаточной функцией

интегральная оценка

зависит от соотношения постоянных времени и.

Использование линейной интегральной оценки J₁возможно только для монотонных процессов и неприемлемо для оценки качества колебательных систем. Для колебательных процессов величина критерия, равная разности между суммой положительных и отрицательных площадей (см. рис. 4.4, б), не будет однозначно связана с действительным качеством регулирования системы.

Например, ухудшение качества переходного процесса при переходе к незатухающим колебаниям будет сопровождаться уменьшение критерия J₁ до нуля. В связи с этим при наличии перерегулирования в переходном процессе и колебательном его характере применяют квадратичную интегральную оценку качества J₂ следующего вида:

.

Величина квадратичной интегральной оценки J₂ равна площади, ограниченной кривой x²(t) (рис. 4.5, а).

В справочной литературе приведены формулы, выражающие величину критерия J₂ непосредственно через коэффициенты дифференциального уравнения замкнутой системы.

Д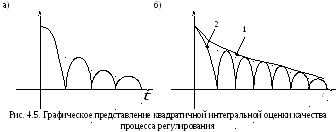анный критерий является наиболее широко используемым интегральным критерием качества, однако в ряде случаев он также не дает достоверной оценки характера переходного процесса. На рис. 4.5, б приведены графикиx²(t) для монотонного процесса (кривая 1) и колебательного процесса (кривая 2). Очевидно, что значение критерия J₂ для колебательного процесса будет меньше, в то время как более предпочтительным является монотонный процесс: ему соответствует плавное изменение выходного сигналы и отсутствие значительных динамических воздействий в системе.

Недостатки рассмотренных интегральных оценок качества обусловили использование обобщенного (улучшенного) интегрального критерия, имеющего в простейшем случае следующий вид:

.

Использование интегральной оценки J₃ позволяет обеспечить в системе быстро затухающий, но достаточно плавный процесс, поскольку наличие в подынтегральном выражении слагаемого ограничивает скорость изменения регулируемой величины, снижая колебательность системы. Чем больше коэффициент , тем значительнее влияние указанного слагаемого, тем более плавным будет переходный процесс, но зато и более длительным.

В качестве интегральных критериев используются и функционалы более общего вида. Иногда в выражении интегральной оценки вводится время t в явном виде.

Наиболее широко интегральные критерии применяются в теории оптимальных систем автоматического управления.

Вопросы для самопроверки

1. Назовите основные показатели качества процесса регулирования, определяемые по переходной функции системы.

2. Как по виду переходной функции системы определяется время регулирования?

3. Что характеризует величина перерегулирования?

4. Что называется нормированной амплитудно-частотной характеристикой системы?

5. Как связана ширина полосы пропускания системы с ее быстродействием?

6. Укажите диапазон изменения значений показателя колебательности, для которых качество регулирования считается удовлетворительным?

7. Какими критериями оценивается качество переходных процессов в зависимости от расположения полюсов передаточной функции замкнутой системы?

8. К каким системам при оценке качества их переходных процессов можно применять линейную интегральную оценку?

5. Оценка точности сАу

5.1. Стационарные режимы сау. Передаточные функции статических и астатических систем

Режим, в котором находится САУ после завершения переходного процесса, вызванного внешними воздействиями или изменением параметров системы, называется стационарным (установившимся). Различают два вида стационарного режима САУ: статический и динамический.

Стационарный статический режим (статика) – это режим, при котором система находится в состоянии покоя. Если же система находится в установившемся вынужденном движении, обусловленном соответствующим внешним воздействием, то такой ее стационарный режим называется динамическим.

Как уже отмечалось, САУ подразделяются на статические и астатические. Установим, какими особенностями должны обладать передаточные функции таких систем.

Передаточная функция замкнутой системы с единичной отрицательной обратной связью (рис. 5.1) равна:

,

где – передаточная функция разомкнутой системы.

С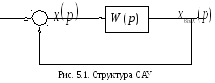игнал– ошибка регулирования.

Передаточная функция такой системы по ошибке:

.

Установившееся значение ошибки регулирования, определенное по теореме о конечном значении, равно:

.

Если на вход системы подан единичный ступенчатый сигнал x_вх(t) = 1(t), изображение по Лапласу которого:

,

то

. (5.1.)

Из выражения (5.1.) следует, что статическая ошиб­ка равна нулю, если передаточная функция по ошибке со­держит в числителе сомножитель p^υ, в про­тивном случае статическая ошибка не равна нулю. Указанное требования к нулям передаточной функции по ошибке равносильно тому, что передаточная функция разомкнутой системы должна иметь нулевой полюс кратностиυ. Величина υ определяет порядок астатизма системы.

Рассмотрим статическую систему, передаточную функцию которой в разомкнутом состоянии запишем в виде:

,

где ;.

Тогда передаточная функция по ошибке:

.

В случае единичного ступенчатого входного сигнала величина установившейся ошибки (такая ошибка называется ошибкой по положению), в соответствии с выражением (5.1) будет равна:

. (5.2)

Передаточная функция разомкнутой системы с астатизмом первого порядка:

.

Передаточная функция по ошибке для такой системы будет иметь вид:

.

Если при этом на вход системы подается единичный ступенчатый сигнал, то, в соответствии с выражением (5.1), ошибка по положению будет равна нулю (рис. 5.2, а).

Пусть на вход этой же системы подается линейно-нарастающий сигнал x_вх(t) = at, изображение по Лапласу которого:

.

Т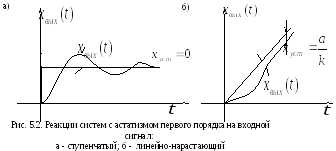огда величина установившейся ошибки (такая ошибка называетсяошибкой по скорости), будет равна (рис. 5.2, б):

.

Нетрудно показать, что установившаяся ошибка астатической системы с астатизмом второго порядка на линейно-нарастающий входной сигнал будет равна нулю.

Из изложенного следует, что для повышения точности САУ необходимо увеличивать коэффициент усиления системы и повышать порядок ее астатизма. Очевидно, что и тот, и другой подход сопряжен с понижением запаса устойчивости системы.