Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.07.2024
Просмотров: 510
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОсновНые понятия и определения теории автоматического управления
1.1. Краткие сведения по истории развития систем автоматического управления
1.2. Обобщенная структурная схема сау
2. Математическое описание линейных сау
2.1. Составление и линеаризация дифференциальных уравнений сау
Основные свойства (теоремы) преобразования Лапласа
Изображения по Лапласу типовых сигналов
2.3. Временные и частотные характеристики звеньев и систем
2.4. Элементарные звенья систем автоматического управления
Пропорциональное (усилительное, безинерционное, масштабирующее) звено
Идеальное дифференцирующее звено
Апериодическое звено первого порядка
Реальное дифференцирующее звено
Инерционное звено второго порядка
Интегро-дифференцирующее звено
Пропорционально-интегральный регулятор (пи-регулятор)
2.5. Неминимально-фазовые звенья
2.6. Эквивалентные преобразования структурных схем линейных сау
2.7. Передаточные функции многоконтурных систем
3. Анализ устойчивости линейныхсау
3.1.Понятие устойчивости линейных систем
3.2.Алгебраический критерий устойчивости Гурвица
3.3.Частотные критерии устойчивости Михайлова и Найквиста
3.5.Оценка устойчивости по логарифмическим амплитудно- и фазо-частотным характеристикам
3.6.Устойчивость систем с запаздыванием
4. Качество динамических характеристик сау
4.1. Показатели качества процесса регулирования
4.2. Частотные критерии качества
4.3. Корневые критерии качества
4.4. Интегральные критерии качества
5.1. Стационарные режимы сау. Передаточные функции статических и астатических систем
5.2. Коэффициенты ошибки системы
5.3. Системы комбинированного управления
6. Анализ сау в пространстве состояния
6.1. Основные положения метода переменных состояния
6.2. Способы построения схем переменных состояния
Метод прямого программирования
Метод параллельного программирования
Метод последовательного программирования
6.3. Решение уравнений состояния линейных стационарных сау. Вычисление фундаментальной матрицы
Последовательные корректирующие звенья
Параллельные корректирующие звенья
7.2. Частотный метод синтеза корректирующих устройств
Построение лах в низкочастотном диапазоне
Построение лах в среднечастотном диапазоне
Зависимость колебательности от значений hи h1
Построение лах в высокочастотном диапазоне
7.3. Последовательные корректирующие устройства
7.4. Параллельные корректирующие устройства
7.5. Техническая реализация корректирующих звеньев
Пассивные четырехполюсники постоянного тока
Пассивные корректирующие четырехполюсники
Активные корректирующие звенья
Активные четырехполюсники постоянного тока
8. Нелинейные системы автоматического управления
8.1. Особенности нелинейных систем и методы их анализа
8.2. Исследование нелинейных систем на фазовой плоскости
8.3. Метод гармонической линеаризации нелинейных звеньев
Коэффициенты гармонической линеаризации типовых нелинейностей
8.5. Методы определения параметров автоколебаний
Задание для расчета линейной caу
Варианты задания для расчета линейной сау
Варианты передаточных функций линейной сау
Задание для расчета нелинейной сау
Варианты задания для расчета нелинейной сау
Варианты структурных схем нелинейных систем Варианты статических характеристик нелинейного элемента
8. Нелинейные системы автоматического управления
8.1. Особенности нелинейных систем и методы их анализа
Система автоматического регулирования является нелинейной, если для нее не выполняется принцип суперпозиции, и сигналы в системе связаны между собой нелинейными дифференциальными уравнениями. Строго говоря, линейных САУ не существует, так как характеристики реальных устройств нелинейны и некоторые из них не могут быть линеаризованы, а при больших отклонениях сигналов от установившихся значений приходится учитывать нелинейные свойства и элементов САУ, допускающих линеаризацию.
Причиной
нелинейности САУ может быть то, что
некоторые сигналы или их производные
входят в математическое описание системы
не в первой степени или имеется
произведение сигналов, а также то, что
коэффициенты уравнений изменяются во
времени или являются функциями сигналов
и их производных. Очень часто нелинейность
системы обусловлена наличием в ней
звеньев, у которых выходной и входной
сигналы связаны между собой существенной,
т.е. неподдающейся линеаризации,
статической нелинейной зависимостью
вида:
![]() .
К числу таких звеньев относятся так
называемыетиповые
нелинейности
(табл. 8.1).
.
К числу таких звеньев относятся так
называемыетиповые
нелинейности
(табл. 8.1).
Во всех перечисленных случаях процессы, протекающие в САУ, описываются нелинейными дифференциальными уравнениями, что существенно усложняет их анализ. К сигналам в нелинейной системе неприменимы преобразования Лапласа или Фурье в обычном виде. В отличие от линейных САУ нелинейная система может иметь несколько состояний устойчивого или неустойчивого равновесия, причем области устойчивости определяются не только параметрами системы, но и значениями начальных условий.
Нелинейная система может находиться не только в равновесно сходящемся процессе, но и в устойчивом установившемся периодическом режиме, называемом режимом автоколебаний. В переходном колебательном процессе в нелинейной системе изменяется не только амплитуда, но и частота колебаний.
При описании нелинейных САУ сначала составляют дифференциальные уравнения для каждого звена системы. При этом характеристики звеньев, не являющихся существенно нелинейными, линеаризуются. В результате, получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы САУ, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть.
Существует достаточно большое число методов, позволяющих решать задачи анализа и синтеза нелинейных систем, например: метод фазовой плоскости; метод кусочно-линейной аппроксимации; метод гармонической линеаризации; метод статистической линеаризации.
Метод
фазовой плоскости
применяется
для анализа нелинейных систем, порядок
которых не выше второго. На плоскости
с координатами
![]() и
и![]() ,
где
,
где![]() – ошибка системы или какой-либо другой
сигнал, строится траектория движения
системы. Плоскость и траекторию движения
систем называют фазовыми. По характеру
фазовой траектории оценивается
качество работы системы.
– ошибка системы или какой-либо другой
сигнал, строится траектория движения
системы. Плоскость и траекторию движения
систем называют фазовыми. По характеру
фазовой траектории оценивается
качество работы системы.
Метод кусочно-линейной аппроксимации используется в том случае, когда нелинейная часть системы безынерционна, и ее характеристика может быть аппроксимирована прямолинейными участками. На каждом таком участке процессы в системе описываются линейными дифференциальными уравнениями, решение которых может быть найдено. В точках излома нелинейной характеристики решения «сшиваются»: значения переменных в конце данного участка принимаются за начальные условия для последующего участка. Таким образом удается построить фазовую траекторию движения системы.
Метод гармонической линеаризации базируется на замене нелинейного элемента линейным звеном, параметры которого определяются при синусоидальном входном сигнале из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все гармонические составляющие выходного сигнала, кроме первой гармоники.
Метод статистической линеаризации является приближенным и применим для систем произвольного порядка. Он основан на замене нелинейного элемента линейным звеном, коэффициенты передачи которого по математическому ожиданию и случайной составляющей сигнала на входе нелинейного элемента определяются из условия статистической эквивалентности нелинейного звена линейному звену.
Рассмотрим описание динамики САУ на фазовой плоскости и использование метода гармонической линеаризации для широко распространенного класса нелинейных систем, характеризующегося следующими особенностями:
структура системы представляет собой соединения из двух частей (рис. 8.1) – линейной части (ЛЧ), описываемой линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами, и нелинейного элемента (НЭ);
н
 елинейный
элемент является безынерционным, и его
входной
елинейный
элемент является безынерционным, и его
входной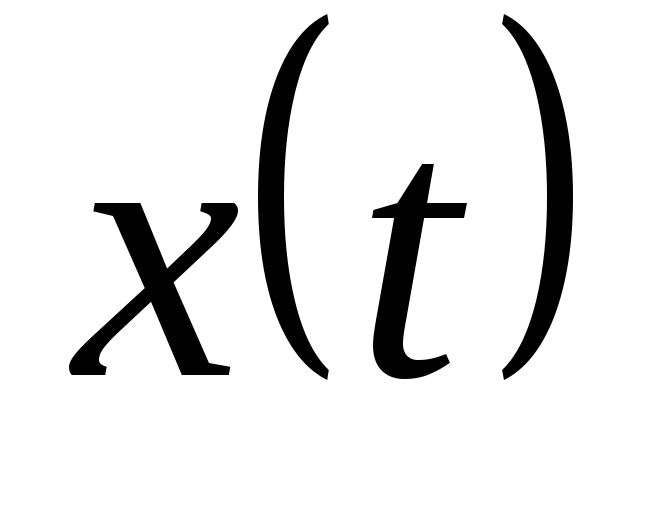 и выходной
и выходной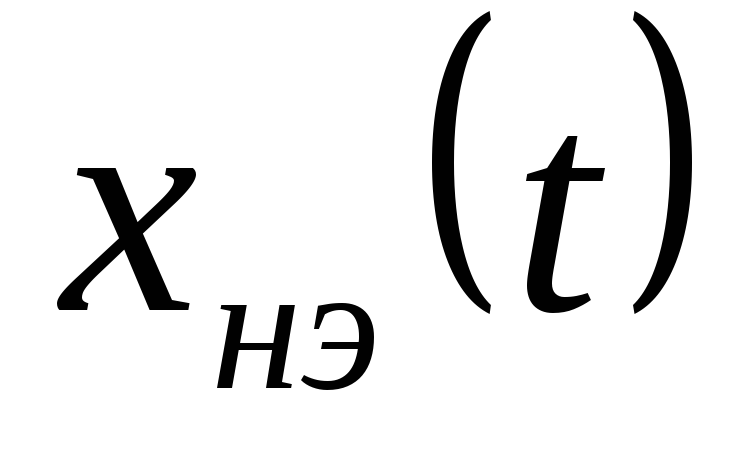 сигналы связаны между собой некоторой
статической зависимостью:
сигналы связаны между собой некоторой
статической зависимостью:
![]() .
.
Если система содержит несколько нелинейных элементов, соединенных между собой параллельно, последовательно или по схеме обратной связи, то в ряде случаев удается заменить эти нелинейные элементы одним с результирующей статической характеристикой.
На
рис. 8.2, а приведена структура системы,
состоящая из двух параллельно включенных
нелинейных звеньев, а на рис. 8.2, б
проиллюстрирована методика определения
результирующей статической характеристики
![]() .
Для ее построения достаточно сложить
ординаты нелинейных характеристик
.
Для ее построения достаточно сложить
ординаты нелинейных характеристик![]() и
и![]() .
.
Рассмотрим
структуру системы, состоящую из двух
последовательно соединенных статических
нелинейных звеньев (рис. 8.3, а). Методика
построения результирующей нелинейной
характеристики
![]() проиллюстрирована на рис. 8.3, б. В первом
квадранте построена статическая
характеристика первого нелинейного
звена
проиллюстрирована на рис. 8.3, б. В первом
квадранте построена статическая
характеристика первого нелинейного
звена![]() ,
а во втором квадранте – характеристика
,
а во втором квадранте – характеристика![]() второго
звена, но
так, ч
второго
звена, но
так, ч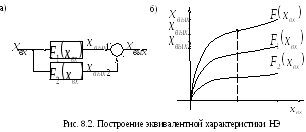 то
ее оси повернуты на
то
ее оси повернуты на![]() :
ось
:
ось![]() совпадает с положительной полуосью
ординат, а ось
совпадает с положительной полуосью
ординат, а ось![]() направлена по отрицательной полуоси
абсцисс. Значению
направлена по отрицательной полуоси
абсцисс. Значению![]()
![]() входного сигнала (точка 1 на оси
входного сигнала (точка 1 на оси![]() )
соответствует значение
)
соответствует значение![]() на выходе первого нелинейного элемента
(точка 2).
на выходе первого нелинейного элемента
(точка 2).
П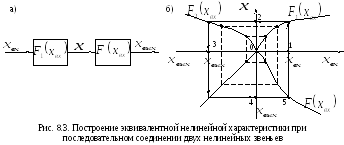 ри
таком значении сигнала на входе второго
нелинейного элемента сигнал на выходе
системы равен:
ри
таком значении сигнала на входе второго
нелинейного элемента сигнал на выходе
системы равен:![]() (точка 3). Очевидно, что величины
(точка 3). Очевидно, что величины![]() и
и![]() представляют собой соответственно
абсциссу и ординату одной из точек на
результирующей нелинейной характеристике
представляют собой соответственно
абсциссу и ординату одной из точек на
результирующей нелинейной характеристике![]() .
.
Но
удобнее построить эту характеристику
в четвертом квадранте, для чего точка
3 с помощью биссектрисы третьего
квадранта отображается в точку 4 на
отрицательной полуоси ординат. Поскольку
расстояния от начала координат до точек
3 и 4 одинаковы, точка 5 принадлежит
эквивалентной нелинейной статической
характеристике
![]() .
Находя аналогичным способом ряд точек
и соединяя их плавной кривой, получаем
результирующую характеристику:
.
Находя аналогичным способом ряд точек
и соединяя их плавной кривой, получаем
результирующую характеристику:![]() .
.
Наиболее
просто строится характеристика
последовательного соединения трех
нелинейных звеньев. Характеристика
![]() располагается
в первом квадранте, а характеристики
располагается
в первом квадранте, а характеристики
![]() и
и![]() ,
с соответствующим поворотом осей, –
во втором и в третьем квадрантах (рис.
8.4).
,
с соответствующим поворотом осей, –
во втором и в третьем квадрантах (рис.
8.4).
В
замкнутой системе (рис. 8.5, а) нелинейный
элемент со статической нелинейностью
![]() ,
охвачен отрицательной обратной связью.
При этом канал обратной связи также
образует нелинейный элемент со своей
статической нелинейностью
,
охвачен отрицательной обратной связью.
При этом канал обратной связи также
образует нелинейный элемент со своей
статической нелинейностью![]() .
.
П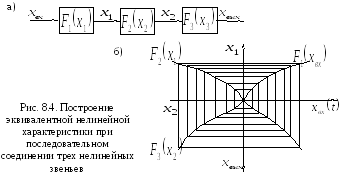 роиллюстрируем
методику построения результирующей
характеристики такой системы (рис. 8.5,
б). В первом квадранте строится
характеристика
роиллюстрируем
методику построения результирующей
характеристики такой системы (рис. 8.5,
б). В первом квадранте строится
характеристика![]() ,
а во втором (с поворотом осей на 900
против часовой стрелки) строится
характеристика
,
а во втором (с поворотом осей на 900
против часовой стрелки) строится
характеристика
![]() .
.
Н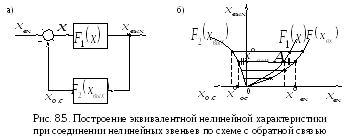 а
характеристике
а
характеристике![]() выбирается произвольная точкаА.
Координаты этой точки (
выбирается произвольная точкаА.
Координаты этой точки (![]() )
– это соответствующие друг другу
значения входного и выходного сигналов
нелинейности в прямом канале системы.
Сигнал
)
– это соответствующие друг другу
значения входного и выходного сигналов
нелинейности в прямом канале системы.
Сигнал![]() является входным сигналом нелинейного
звена в обратной связи системы, а его
значению
является входным сигналом нелинейного
звена в обратной связи системы, а его
значению![]() на выходе второй нелинейности будет
соответствовать сигнал равный:
на выходе второй нелинейности будет
соответствовать сигнал равный:![]() .
.
В случае отрицательной обратной связи
![]()
т.е. указанному значению выходного сигнала системы, соответствует входной сигнал равный:
![]()
Следовательно,
для построения первой точки результирующей
нелинейности системы
![]() достаточно
точкуА
переместить вправо параллельно оси
абсцисс на расстояние равное значению
достаточно
точкуА
переместить вправо параллельно оси
абсцисс на расстояние равное значению
![]()
Очевидно,
что в случае положительной обратной
связи, точку
А необходимо
было бы переносить на такое же расстояние
влево. Осуществив указанную процедуру
многократно, можно по полученным точкам
построить результирующую характеристику:
![]() .
.
Если же между нелинейными элементами имеются разделяющие их инерционные линейные звенья, то САУ уже не удается свести к рассматриваемому в данном пособии классу систем.