Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc

с дифференцирующими свойствами в среднечастотном диапазоне (>). Параметры корректирующего звена опре­деляются следующим образом:

; .

Значения сопрягающих частот и , а также ве­личинаберутся из рис. 7.7.

Для уточнения действительного запаса устойчивости по модулю и фазе синтезированной системы на рис.7.7 построена логарифмическая фазо-частотная характеристика. Как видно из рис. 7.7, запасы устойчивости по фазе и по модулю скорректи­рованной системы больше соответствующих запасов устойчивости исходной системы.

Из рассмотренного примера следует, что достоинство коррекции с помощью последовательных дифференцирующих устройств заключается в том, что при обеспечении требуемого запаса устойчивости одновременно увеличивается частота среза и возмож­но увеличение коэффициента усиления системы, в ре­зультате чего умень­шаются время регулирования и установившаяся ошибка.

Однако после­довательная коррекция с помощью дифференцирующих устройств имеет и не­достатки, заключающиеся в значительном увеличении усиления в области высоких частот. Если при этом на полезный входной сигнал системы накладываются высокочастотные помехи, степень их подавления в скорректированной системе будет ниже, чем в нескорректированной. Помехоустойчивость системы может быть повышена путем снижения коэффициента усиления системы, но это приведет к снижению точности регулирования.

Для исключения существенного ослабления коэффициента усиления системы на низких частотах в качестве последовательного корректирующего звена можно использовать интегро-дифференцирующее зве­но с преобладающими интегрирующими свойствами, т.е. при <(рис. 7.8).

Как вид­но из рис. 7.8, исходная нескорректированная система не только не обеспечи­вает требуемого качества регулирования, но даже яв­ляется неустойчивой. Без корректирующего устройства требуемый запас устойчивости в системе можно обеспечить только за счет большого снижения коэффициента усиления системы, что яв­ляется нежелательным.

Желаемую ЛАХ скорректированной системы можно получить при последовательном включении корректирую­щего устройства с интегрирующими свойствами. Из рис. 7.8 следует, что наряду с относительным уве­личением коэффициента усиления системы на низких ча­стотах существенно умень­шено усиление на высоких частотах и тем самым ослаблено влияние высокочастотных помех.

Н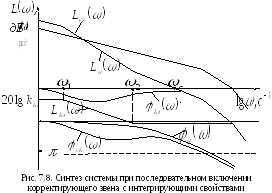едостатком таких корректирующих устройств является то, что при их использовании уменьшается частота среза и, следователь­но, длительность переходных процессов в системе уве­личивается.

При решении практических инженерных задач по син­тезу структуры САУ широкое применение находят по­следовательные корректирующие устройства в виде ком­бинированных интегро-дифференцирующих звеньев.

Пример синтеза желаемых логарифмических частот­ных характеристик системы с помощью последовательного комбинированного интегро-дифференцирующего звена представлен на рис. 7.9.

Из рис. 7.9 следует, что при правильно выбранных параметрах корректирую­щего устройства можно обеспечить требуемую точность регулирования в установившихся режимах и одновременно повысить качество переходного процесса, по сравнению с исходной системой. Передаточная функция корректирующего звена с ЛАХ , приведенной на рис. 7.9, равна:

.

При выборе коэффициента усиления корректирующе­го устройства следует исходить из условия обеспечения требуемой точности в установившихся режимах скоррек­тированной системы. Так, если коэффициент передачи ис­ходной нескорректированной разомкнутой системы равен, а требуемый ко­эффициент передачи скорректированной системы равен , то коэффициент передачи корректирующего устрой­ства должен быть равен:

.

Постоянные времени корректирующего устройства инеобходимо выбирать так, что­бы частоты сопряженияибыли бы значительно меньше частоты срезаскорректирован­ной системы. Этим обеспечивается сдвиг интервала частот, в кото­ром корректирующее устройство создает отставание по фазе в безопасную зону слева от частоты среза.

Частоты сопряжения идолжны быть такими, чтобы частота срезарас­полагалась бы примерно в середине интервала частот<<. В этом случае максимальное опереже­ние, создаваемое корректирующим устройством, будет в области частоты среза, что обеспечивает в скорректированной системе наибольший запас устойчивости по фа­зе.

Зачастую не все из перечисленных рекомендаций по выбору параметров корректирующего устройства удается удовлетворить в полной мере. Поэтому необходимо построить ЛАХ скор­ректированной системы с учетом фактических логариф­мических частотных характеристик корректирующего устройства и проверить, например, путем моделирования системы на ЭВМ, удовлетворяет ли САУ предъявляемым требованиям к качеству регулирования.

7.4. Параллельные корректирующие устройства

Из выражения (7.2) следует, что желае­мая АФХ разомкнутой скорректированной системы при параллельном включении корректирующего устройства описывается выражением:

. (7.10)

В интервале частот, в котором << 1, выражение (7.10) можно приближенно записать в виде:

. (7.11)

Из выражения (7.11) следует, что в этом диапазоне частот параллельное корректирующее устройство прак­тически не влияет на динамические свойства исходной системы.

В интервале частот, в котором >>1, выражение (7.10) приближенно можно записать в виде:

. (7.12)

Из выражения (7.12) следует, что в этом интервале частот влияние звеньев, охваченных корректирующим устройством в виде обратной связи, на динамические свойства системы практически исключается. Следовательно, корректирующей обратной связью следует охватывать такие звенья системы, которые су­щественно ухудшают динамические свойства системы.

На основании выражения (7.12) можно записать выражения для логарифмическиих амплитудно- и фазо-частотной характеристик:

; (7.13)

, (7.14)

откуда частотные характеристики корректирующего устройства:

; (7.15)

. (7.16)

По полученным частотным характеристикам коррек­тирующего устройства подбирается наиболее простое в техническом отношении его исполнение.

Если частотные характеристики выбранного коррек­тирующего устройства несколько отличаются от расчет­ных, то необходимо построить ЛАХ скорректированной системы и проверить, обеспечивается ли в системе тре­буемое качество регулирования.

Если при этом требуемое качество регулирования не обеспечивается, то можно дополнительно включить по­следовательно корректирующие устройства. В этом случае при синтезе последовательного корректи­рующего устройства в качестве исходной следует прини­мать систему, скорректированную параллель­ным корректирующим устройством.

Задача синтеза САУ всегда решается неоднозначно, т.е. структура передаточной функции и параметры корректирующего звена могут варьироваться в определенных пределах. Поэтому желательно выполнение поставленной задачи в нескольких вариантах с тем, чтобы из них выбрать наиболее простой для технической реализации, на­дежности функционирования системы, качества регули­рования и удобства эксплуатации.

7.5. Техническая реализация корректирующих звеньев

Корректирующие звенья могут быть выполнены из различных по физической природе элементов: электрических, механических, гидрав­лических и т. д. Наиболее просто реализуются пассивные и активные корректиру­ющие звенья (четырехполюсники) на базе RС- и RL-элементов.

Пассивные четырехполюсники постоянного тока

Пассивные четырехполюсники постоянного тока – это электрические цепи из резисторов, конденсаторов и индуктивностей. Общая схема пассивного четырехполюсника показана на рис. 7.10. Если его выходное напряжение приложено к нагрузке с бесконечно большим полным сопротивлением, то передаточная функция пассивного четырехполюсника равна:

, (7.17)

где и– изображения по Лапласу входного и выходного напряжений четырехполюсника;– операторы сопротивлений четырехполюсника;– соответственно активные сопротивления, емкости и индуктивности.

Изменяя вид операторов сопротивлений и значения, можно получить большое количество четырехполюсников, описываемых передаточными функциями (7.17). Стоимость пассивных четырехполюсников низкая, а стабильность параметров достаточно высокая. Этими достоинствами объясняется широкое использование их в системах автоматического регулирования в качестве корректирующих звеньев.