Файл: Г.М. Гринфельд ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ уч. пособие.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.07.2024
Просмотров: 504
Скачиваний: 3
СОДЕРЖАНИЕ
1. ОсновНые понятия и определения теории автоматического управления
1.1. Краткие сведения по истории развития систем автоматического управления
1.2. Обобщенная структурная схема сау
2. Математическое описание линейных сау
2.1. Составление и линеаризация дифференциальных уравнений сау
Основные свойства (теоремы) преобразования Лапласа
Изображения по Лапласу типовых сигналов
2.3. Временные и частотные характеристики звеньев и систем
2.4. Элементарные звенья систем автоматического управления
Пропорциональное (усилительное, безинерционное, масштабирующее) звено
Идеальное дифференцирующее звено
Апериодическое звено первого порядка
Реальное дифференцирующее звено
Инерционное звено второго порядка
Интегро-дифференцирующее звено
Пропорционально-интегральный регулятор (пи-регулятор)
2.5. Неминимально-фазовые звенья
2.6. Эквивалентные преобразования структурных схем линейных сау
2.7. Передаточные функции многоконтурных систем
3. Анализ устойчивости линейныхсау
3.1.Понятие устойчивости линейных систем
3.2.Алгебраический критерий устойчивости Гурвица
3.3.Частотные критерии устойчивости Михайлова и Найквиста
3.5.Оценка устойчивости по логарифмическим амплитудно- и фазо-частотным характеристикам
3.6.Устойчивость систем с запаздыванием
4. Качество динамических характеристик сау
4.1. Показатели качества процесса регулирования
4.2. Частотные критерии качества
4.3. Корневые критерии качества
4.4. Интегральные критерии качества
5.1. Стационарные режимы сау. Передаточные функции статических и астатических систем
5.2. Коэффициенты ошибки системы
5.3. Системы комбинированного управления
6. Анализ сау в пространстве состояния
6.1. Основные положения метода переменных состояния
6.2. Способы построения схем переменных состояния
Метод прямого программирования
Метод параллельного программирования
Метод последовательного программирования
6.3. Решение уравнений состояния линейных стационарных сау. Вычисление фундаментальной матрицы
Последовательные корректирующие звенья
Параллельные корректирующие звенья
7.2. Частотный метод синтеза корректирующих устройств
Построение лах в низкочастотном диапазоне
Построение лах в среднечастотном диапазоне
Зависимость колебательности от значений hи h1
Построение лах в высокочастотном диапазоне
7.3. Последовательные корректирующие устройства
7.4. Параллельные корректирующие устройства
7.5. Техническая реализация корректирующих звеньев
Пассивные четырехполюсники постоянного тока
Пассивные корректирующие четырехполюсники
Активные корректирующие звенья
Активные четырехполюсники постоянного тока
8. Нелинейные системы автоматического управления
8.1. Особенности нелинейных систем и методы их анализа
8.2. Исследование нелинейных систем на фазовой плоскости
8.3. Метод гармонической линеаризации нелинейных звеньев
Коэффициенты гармонической линеаризации типовых нелинейностей
8.5. Методы определения параметров автоколебаний
Задание для расчета линейной caу
Варианты задания для расчета линейной сау
Варианты передаточных функций линейной сау
Задание для расчета нелинейной сау
Варианты задания для расчета нелинейной сау
Варианты структурных схем нелинейных систем Варианты статических характеристик нелинейного элемента
При описании системы в пространстве состояния целесообразно разделить все сигналы, характеризующие поведение системы, на три группы:
входные сигналы или входные воздействия
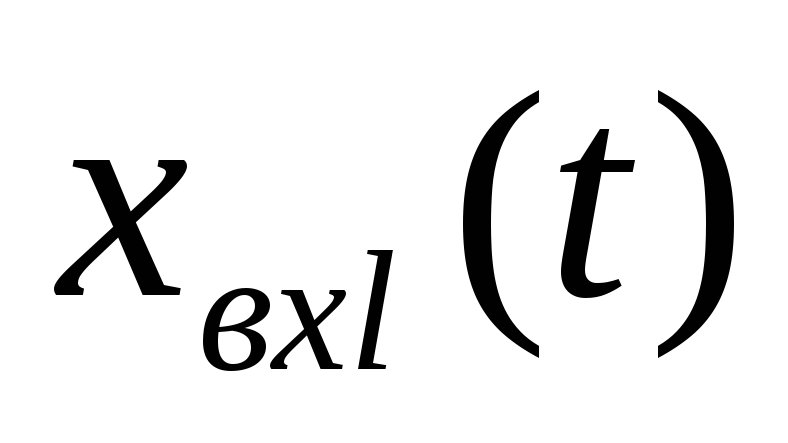 ,
приложенные к исследуемой системе со
стороны других систем,
,
приложенные к исследуемой системе со
стороны других систем,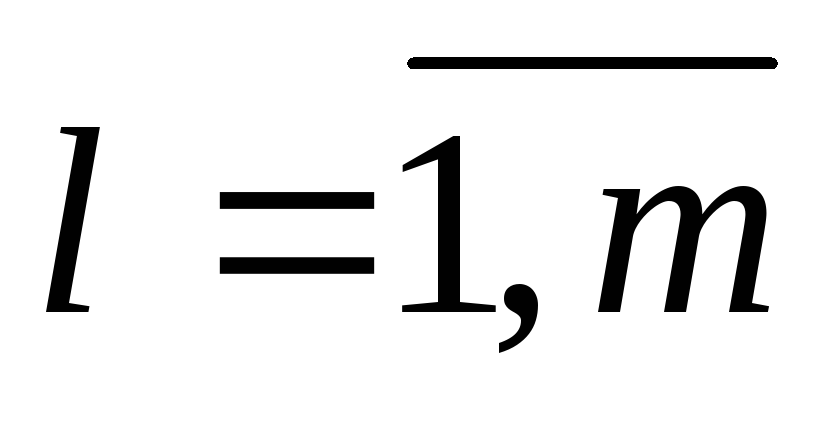 ;
;выходные сигналы
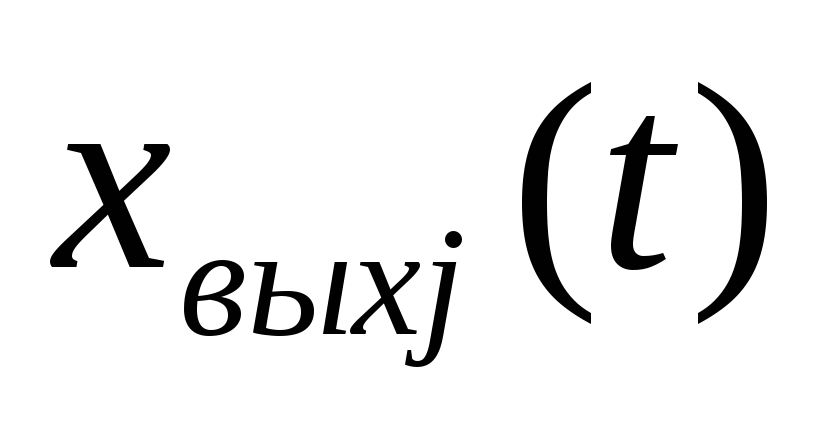 ,
характеризующие
реакцию системы на указанные входные
воздействия,
,
характеризующие
реакцию системы на указанные входные
воздействия,
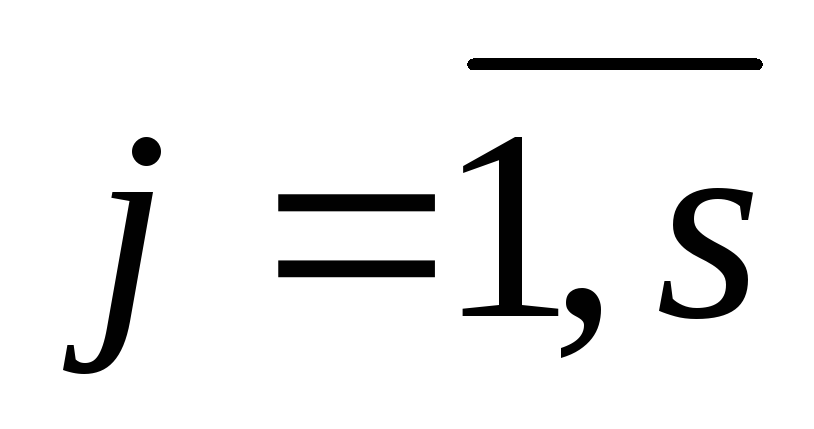 ;
;промежуточные переменные
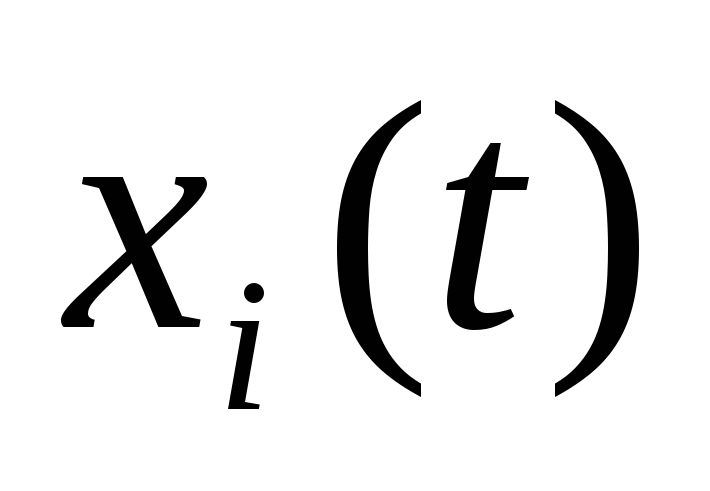 ,
характеризующие внутреннее состояние
системы,
,
характеризующие внутреннее состояние
системы, .
.
Для удобства описания каждую группу переменных можно представить в виде вектора (матрицы-столбца):
Xвх(t)
=
![]() – вектор входных воздействий;
– вектор входных воздействий;
Xвых(t)=
![]() – вектор выходных переменных системы;
– вектор выходных переменных системы;
X(t)
=
![]() – вектор переменных состояния системы.
– вектор переменных состояния системы.
Приведенная
классификация сигналов в системе
является в определенной степени условной,
так, некоторые переменные состояния
![]() могут
совпадать с выходнымисигналами
могут
совпадать с выходнымисигналами
![]() ,
но в общем случае между ними существует
следующая зависимость:
,
но в общем случае между ними существует
следующая зависимость:
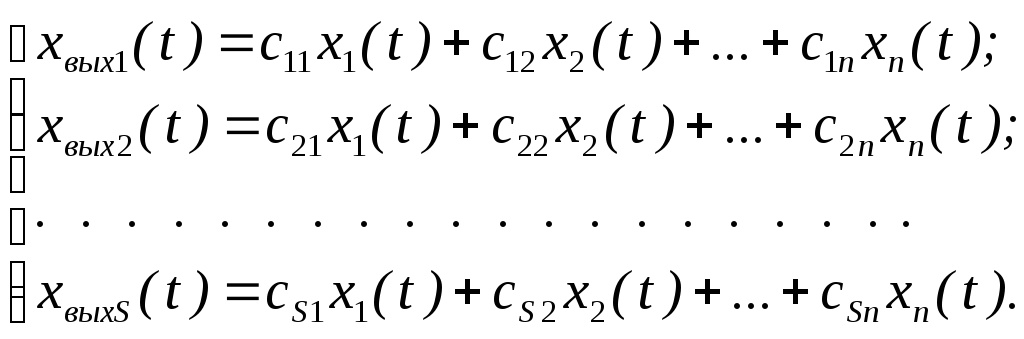 (6.1)
(6.1)
В пространстве состояния, осями координат которого являются переменные состояния, каждому моменту времени соответствует вектор X(t). Величина и положение этого вектора с течением времени изменяются, в результате чего конец вектора X(t) описывает кривую, называемую траекторией движения системы в пространстве состояний.
Динамика
линейной стационарной САУ
![]() -го
порядка может быть описана системой
-го
порядка может быть описана системой![]() линейных дифференциальных уравнений:
линейных дифференциальных уравнений:
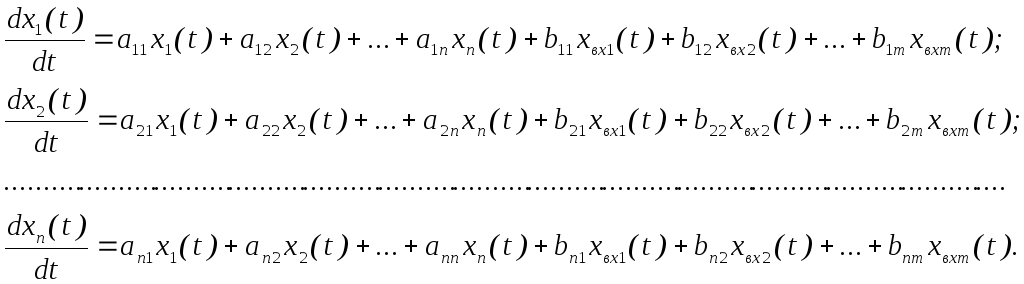 (6.2)
(6.2)
Систему уравнений (6.2) можно записать в виде следующего матричного (векторного) дифференциального уравнения:
![]() ,
(6.3)
,
(6.3)
где
А – матрица
системы
(квадратная
матрица размером
– матрица
системы
(квадратная
матрица размером
![]() );
);
B
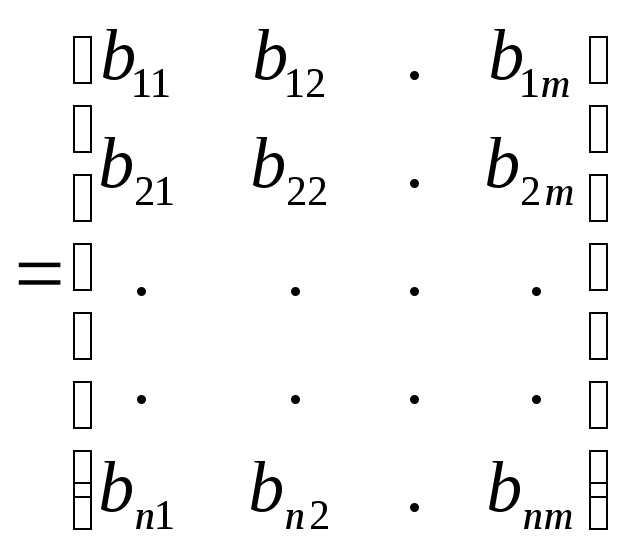 –
матрица
управления
размером
–
матрица
управления
размером
![]() .
.
В матричной форме система уравнений (6.1) примет вид:
![]() ,
(6.4)
,
(6.4)
где
С
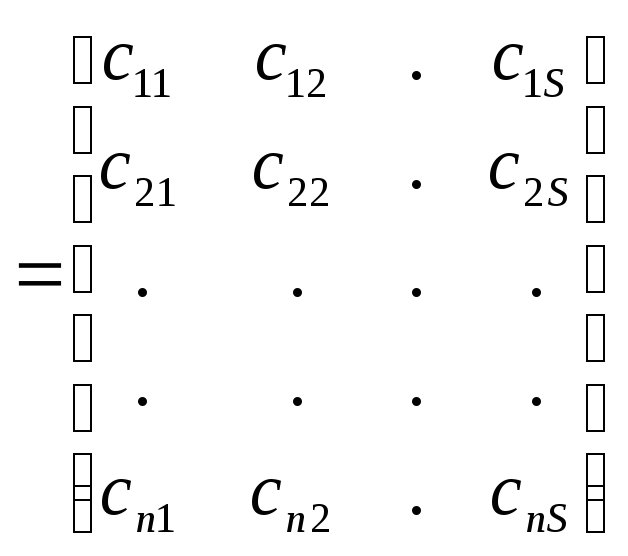 –
матрица
наблюдения
размером
–
матрица
наблюдения
размером
![]() .
.
У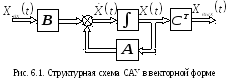 равнения
(6.3) и (6.4) называютуравнениями
состояния системы.
равнения
(6.3) и (6.4) называютуравнениями
состояния системы.
Элементы матрицы системы А определяются структурной схемой системы и значениями ее параметров. Матрица управления В характеризует влияние входных сигналов на переменные состояния, а матрица наблюдения С определяет связь выходных сигналов системы с вектором состояния. Обычно не все составляющие вектора состояния являются наблюдаемыми сигналами, т. е. они не могут быть измерены с помощью каких-либо датчиков, в то время как выходные сигналы всегда наблюдаемы.
На рис. 6.1 показана структурная схема системы, соответствующая векторным уравнениям (6.3) и (6.4); двойные линии на рисунке характеризуют векторный характер сигналов.
Согласно определению понятия состояния системы, в любой момент времени t > t0 состояние системы является функцией начального состояния X(t0) и вектора входа Xвх(t0 , t), т.е.
X(t) = F[X(t0), Xвх(t0 , t)]. (6.5)
Вектор выхода в момент t также однозначно связан с векторами X(t0) и Xвх(t0 , t):
Xвых(t) = R[X(t0), Xвх(t0 , t)]. (6.6)
Приведенные векторные дифференциальные уравнения описывают линейные стационарные САУ. В нестационарных системах элементы матрицы в уравнениях (6.3) и (6.4) являются функциями времени, и векторные дифференциальные уравнения принимают вид:
![]() ;
(6.7)
;
(6.7)
![]() .
(6.8)
.
(6.8)
6.2. Способы построения схем переменных состояния
Набор внутренних переменных системы, определяющих вектор состояния X(t), может быть различным, т.е. для исследуемой системы существует множество групп переменных состояния
X(1)(t)=![]() ,
X(2)(t)=
,
X(2)(t)=![]() ,…,
,…,
таких, что каждая из них описывает состояние полностью, причем любые два вектора X(i)(t) и X(j)(t) из этого множества будут однозначно связаны между собой. Удачный выбор переменных состояния часто приводит к существенному упрощению математического описания САУ.
Естественным является стремление выбрать в качестве составляющих вектора состояния контролируемые выходные сигналы системы, характеризующие качество процесса управления, но их обычно бывает недостаточно для полного математического описания САУ. Выбор вектора переменных состояния осуществляется одним из следующих трех способов, называемых методами программирования:
прямого;
параллельного;
последовательного.
Кроме того, возможны комбинированные способы, когда часть системы строится, например, методом параллельного программирования, а остальная часть – методом последовательного программирования.
Метод прямого программирования
Пусть передаточная функция системы имеет вид:
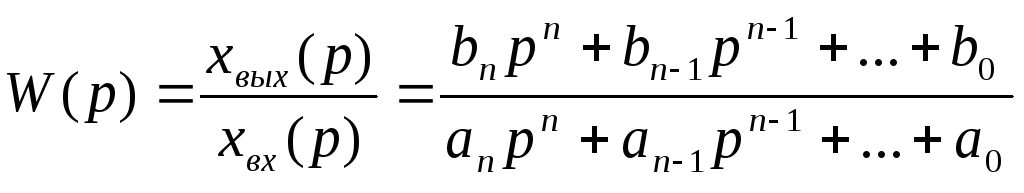 .
(6.9)
.
(6.9)
Разделив
числитель и знаменатель W
(р} на
![]() ,
получим:
,
получим:
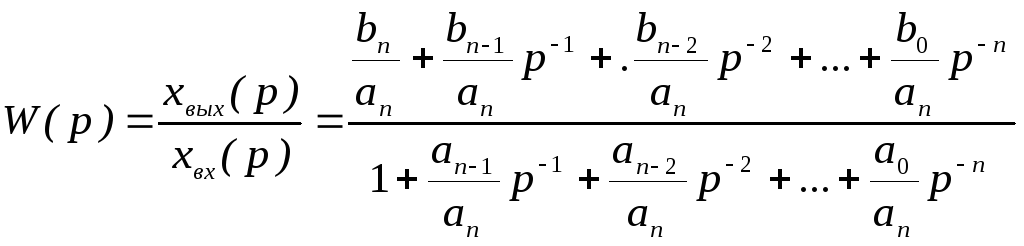 .
.
Выходной сигнал системы равен:
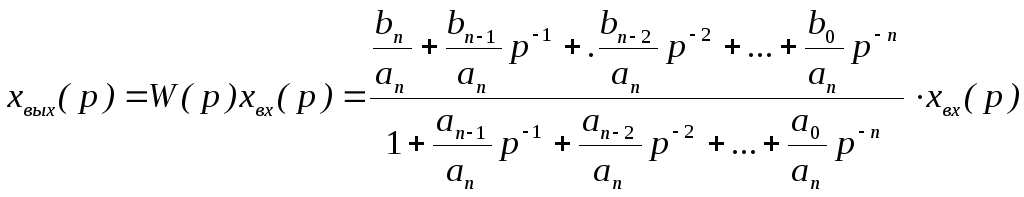 .
.
Введем
в рассмотрение фиктивную переменную
![]() ,
равную:
,
равную:
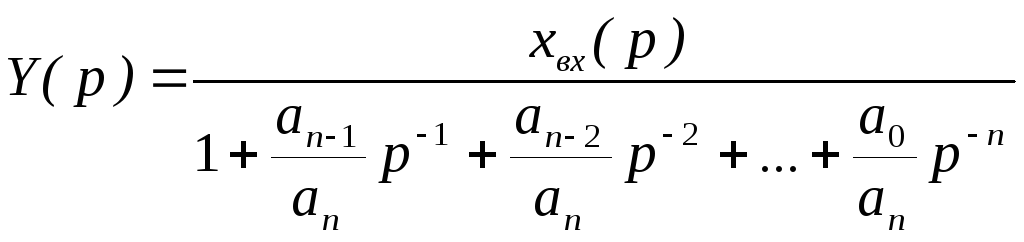 .
.
Преобразуем последнее выражение к виду:
![]()
![]()
![]() .
(6.10)
.
(6.10)
Тогда выходной сигнал системы может быть выражен следующим образом:
![]()
![]() .
(6.11)
.
(6.11)
На
основании выражений (6.10) и (6.11) составим
структурную схему системы (рис. 6.2) с
передаточной функцией (6.9), содержащую
только пропорциональные звенья и
![]() последовательно
соединенных интегрирующих звеньев.
последовательно
соединенных интегрирующих звеньев.
О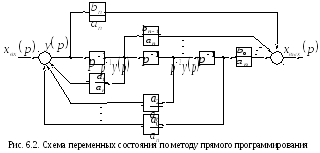 чевидно,
что в качестве переменных состояния,
полностью описывающих поведение такой
системы, могут быть выбраны выходные
сигналы интегрирующих звеньев:
чевидно,
что в качестве переменных состояния,
полностью описывающих поведение такой
системы, могут быть выбраны выходные
сигналы интегрирующих звеньев:
X(t)
=
![]() .
.
Особый интерес представляют схемы переменных состояния простейших звеньев (рис. 6.3) с передаточными функциями вида:
а)
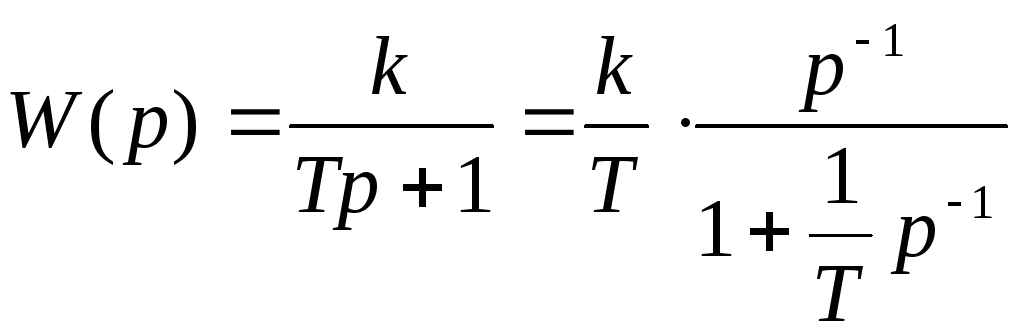 ;
;
б)
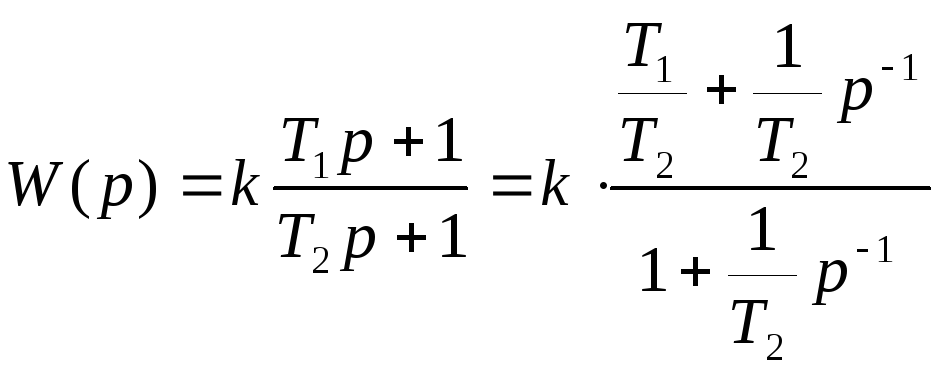 ;
;
в)
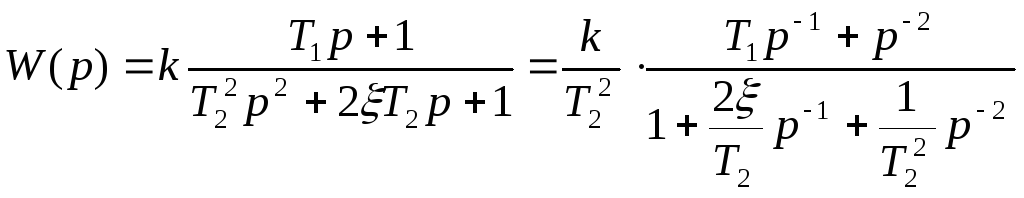 ;
;
г )
)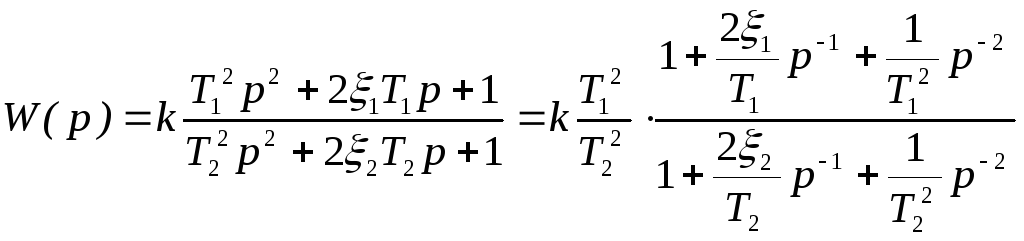 .
.
Метод параллельного программирования
Для
построения схем переменных состояния
способом параллельного программирования
передаточная функция системы (6.9),
имеющая в общем случае
![]() действительных и
действительных и![]() пар
комплексно-сопряженных полюсов (
пар
комплексно-сопряженных полюсов (![]() ),
предварительно должна быть разложена
на сумму простейших дробей, т.е.
представлена в виде:
),
предварительно должна быть разложена
на сумму простейших дробей, т.е.
представлена в виде:
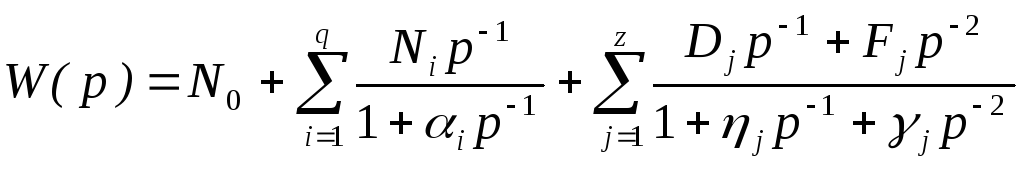 ,
(6.12)
,
(6.12)
где
![]() коэффициенты разложения.
коэффициенты разложения.