Файл: Конспект лекций для студентов специальности 1 48 01 02 Химическая технология органических веществ, материалов и изделий.docx

– магнитный орбитальный момент движения электрона, пропорционально числу m_l – магнитному орбитальному квантовому числу.

Кроме того, любой электрон, в том числе и не связанный с ядром, имеет собственный магнитный момент (спин) m_s = ±1/2:



Согласно уравнению Шредингера, для главного квантового числа (n) возможны только целочисленные значения n = 1,2,3, …
Физический смысл квантовых чисел, связь их с понятиями: энергетический уровень, подуровень(s‑, p-, d‑, f-,..), орбиталь. Форма электронных орбиталей и их пространственная ориентация относительно ядра атома

Состояние электронов с определенным n называют уровнем. Если n = 1, то это первый уровень, если n = 2, то это второй уровень и т.д. Из того, что максимальная величина n не ограничена, следует, что в любом атоме – бесчисленное множество энергетических уровней.

Для орбитального квантового числа (l) возможны целочисленные значения по (n–1) включительно, а также «ноль», т.е. l = 0,1,2,3, …(n–1).

Состояние электронов с определенным l называют подуровнем. Число подуровней определяется величиной n для этого уровня:

– если n = 1 (первый уровень), то возможно только одно значение l = 0, поэтому на первом уровне – только один подуровень;

– если n = 2 (второй уровень), то возможно два значения l = 0 и 1, поэтому на втором уровне – два подуровня.

Легко убедиться, что число подуровней равно величине n: на третьем уровне (n = 3) – три подуровня, на четвертом – четыре и т.д.

Подуровни (s-, p-, d-, f- и т.д.) различаются величиной орбитального квантового числа l: подуровень с l = 0 называют s – подуровнем, l = 1 – p-подуровнем, l = 2 – d-подуровнем, l = 3 – f-подуровнем, (далее, при больших l, символы присваивают в порядке латинского алфавита).

Величина l определяется также формой электронных орбиталей (рисунок 2.1.). Орбитали с равным l, но с разным n (например, 1s и 2s) одинаковы по форме, но различаются размерами: орбитали с большим n имеют больший размер (т.к. при большем n они более удалены от ядра).

Для магнитного орбитального квантового числа (m_l) возможны целочисленные значения от –l до +1, включая «ноль», т.е. всего (2l + 1) значений.

---

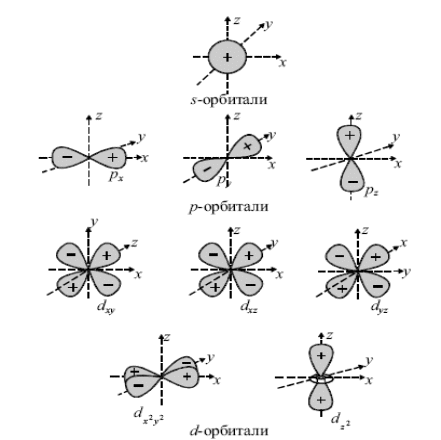
Рисунок 2.1 – Форма атомных орбиталей
Число возможных значений m_l для данного подуровня определяет число вариантов ориентации орбитали в пространстве (и соответственно число этих орбиталей на подуровне). Например, для s-подуровня (l = 0) возможно только одно значение m_l= 0, поэтому на s-подуровне только одна орбиталь. Для p-подуровня l = 1, и для m_l возможны три значения: –1, 0, +1, поэтому на p-подуровне три орбитали, ориентированные вдоль осей XYZ декартовой системы координат (обозначаются, соответственно p_x, p_y, p_z). Легко показать, что на d-подуровне – пять орбиталей, на f- подуровне – семь и т.д. (нечетный ряд).

Еще раз подчеркнем, что изложенные принципы квантования состояний обязательны для электрона, связанного с ядром. Свободные электроны (β-частицы, например) могут иметь любую энергию, не подчиняясь правилам квантования, кроме m_s = ±1/2).

Три квантовых числа (n, l, m_l) однозначно определяют конкретную орбиталь в атоме. Например, если n = 3, l = 1, m_l = 0, то это орбиталь третьего уровня, p-подуровня, ориентированная вдоль оси Z. Если требуется указать «адрес» конкретного электрона в атоме, то кроме «адреса» его орбитали (n, l, m_l) требуется указать знак спина: m_s = +1/2 или m_s = – 1/2.

Принцип Паули. Электронная емкость орбитали, подуровня, уровня

Согласно принципу Паули, в атоме не может быть двух электронов, у которых все четыре квантовых числа были бы одинаковыми.

Пример: Если для одного из электронов в атоме n = 3, l = 1, m_l= 0, m_s = +1/2, то другие электроны должны иметь хотя бы одно квантовое число другое, а именно: или другое n, т.е. находиться на другом уровне, или другое l, т.е. находиться на другом подуровне, или другое m_l, т.е. находиться на другой орбитали, или иметь те же n, l, m_l, но иметь противоположный по знаку спин.

Из последнего варианта следует, что на каждой атомной орбитали, характеризующейся определёнными значениями n, l, m_l, может находиться не более двух электронов, причём спины этих электроновдолжны бытьпротивоположными по знаку.(Так как только в этом случае три квантовых числа, n, l, m_l этих электронов будут одинаковыми, но спины – разными: у одного электрона m_s = +1/2, у другого m_s

---

= –1/2).

Обозначение неспаренного электрона на атомной орбитали, если ms = +1/2

Обозначение двух спаренных электронов с противоположными спинами, находящихся на одной атомной орбитали

Зная число орбиталей на подуровне (одна – на s-, три – на p-, пять – на d- и семь – на f-) и с учетом того, что на одной орбитали может быть не более двух электронов, легко определить, что на s-подуровне быть до двух электронов, на p-подуровне – до 6, на d-подуровне – до десяти и на f-подуровне – до четырнадцати электронов. Соответственно на первом уровне (только 1s-подуровень) может быть один или два электрона; на втором уровне (2s- и 2p- подуровни) – до 8 электронов; на третьем уровне (включающем подуровни s-, p-, d-) может быть до 18 электронов: 2 + 6 + 10.
Относительная энергия уровней и подуровней

Для одноэлектронного атома водорода относительная энергия подуровней определяется, прежде всего, величиной главного квантового числа: меньшую энергию имеет подуровень с меньшим n. В пределах одного и того же уровня энергия подуровней увеличивается в ряду Е_s < Е_p < Е_d < Е_f , и в атоме водорода относительная энергия подуровней будет следующая: 1s2s2p3s3p3d4s4p4d4f5s5p5d5f5g6s…

В многоэлектронных атомах на энергию электронов влияет не только притяжение их к ядру, но и межэлектронное отталкивание. В результате относительная энергия некоторых подуровней меняется по сравнению с атомом водорода.
В многоэлектронных атомах меньшую энергию имеет подуровень с меньшей суммой (n + l); при равной сумме (n + l) меньшую энергию имеет подуровень с меньшим n.
Выпишем последовательность, определенную для атома водорода, и проставим для каждого подуровня сумму (n + l):

1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 5g 6s…

∑(n + l): 1 2 3 3 4 5 4 5 6 7 5 6 7 8 9 6

А теперь, выполнив перестановки в соответствии с приведенными выше правилами, расположим подуровни в порядке увеличения их энергии:

1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d…
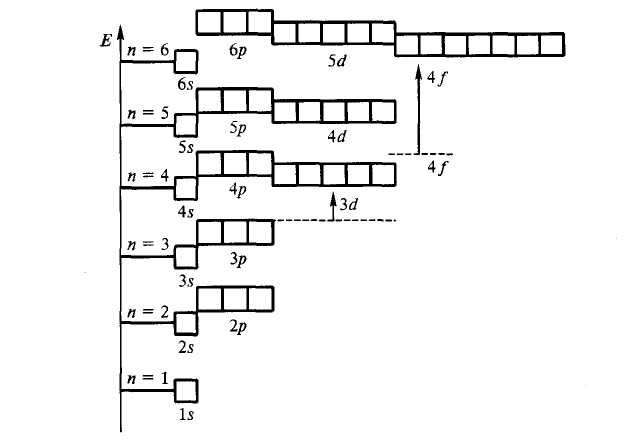На рисунке 2.2 показана энергетическая диаграмма атомных орбиталей многоэлектронного атома.

---

Порядок заполнения электронами орбиталей подуровней, уровней. Электронные и электронно-графические формулы атомов

Порядок заполнения определяется принципом наименьшей энергии: вначале заполняются орбитали, на которых энергия электрона будет меньшей.

При этом кроме приведенного выше ряда относительной энергии подуровней и принципа Паули необходимо учесть правила Гунда: устойчивому состоянию атома соответствует такое распределение электронов в пределах подуровня, при котором абсолютное значение суммарного спина максимально.

Пример: распределить три электрона на p-подуровне в соответствии с правилом Гунда.

а

б

При варианте (б) абсолютная величина суммарного спина равна 3/2; при варианте (а) равна 1/2. Очевидно, что правилу Гунда соответствует вариант (б).

Правило Гунда не запрещает другого распределения электронов в пределах подуровня (на то оно и «правило», а не закон), однако другие варианты возможны при возбуждении атомов (такие варианты встретятся при рассмотрении химических связей в комплексных соединениях).

Распределение электронов по подуровням показывают электронные конфигурации (электронные формулы) атомов. Например, в атоме с зарядом ядра Z = +11 имеются 11 электронов, которые распределятся по подуровням следующим образом: 1s²2s²2p⁶3s¹– это и есть электронная конфигурация (формула) атома с Z = +11.

Что получится для атома с Z = +23?: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d³ – Эта последовательность заполнения соответствует приведенным ранее правилам, но в отличие от предыдущего примера – это пока не еще не электронная формула. Дело в том, что подуровень 3d выше по энергии, чем 4s до тех пор, пока он вакантный. При появлении на 3d первого же электрона энергия его понижается по сравнению с 4s. В результате действительной электронной формулой атома с Z = +23 будет 1s²2s²2p⁶3s²3p⁶3d³4s².

---

Подобные перестановки приходится делать во всех случаях, когда при распределении электронов «последние» оказываются на d- или f-подуровне. По этой причине в таких атомах всех элементов внешние электроны – на s-подуровне.

«Проскок» электрона

«Проскок» проявляется в том, что при заполнении d- или f-подуровней возможен переход на них электрона с внешнего s- подуровня: ns  (n – 1)d.

«Проскок» чаще наблюдается в тех случаях, когда при распределении электронов в атоме на (n–1)d-подуровне оказывается четыре или девять электронов (т.е. не хватает одного электрона до завершения подуровня наполовину или полностью). В результате «проскока» электронные формулы атомов с зарядами ядер, например Z = +24 (Сr) и Z = 29 (Cu) оказываются не 1s²2s²2p⁶3s²3p⁶3d⁴4s² и 1s²2s²2p⁶3s²3p⁶3d⁹4s², а 1s²2s²2p⁶3s²3p⁶3d⁵4s¹ и 1s²2s²2p⁶3s²3p⁶3d¹⁰4s¹ соответственно. Особенно часто «проскок» наблюдается у атомов пятого периода; в атоме палладия – двойной «проскок», и на внешнем 5s-подуровне нет ни одного электрона. Для f-подуровней закономерности более сложные.
Физический смысл Периодического закона Д.И.Менделеева. Cтруктура таблицы элементов

Физический смысл периодического закона заключается в том, что с изменением зарядов ядер атомов (и соответственно общего числа электронов в атоме) периодически повторяется электронное строение внешнего (валентного) уровня атомов, а вследствие этого периодически повторяются химические свойства элементов и их соединений.

Поэтому свойства атомов элементов, образуемых ими простых веществ и других химических соединений находятся в периодической зависимости от зарядов ядер атомов (современная формулировка Периодического закона).

Периодическая таблица элементов является графическим изображением периодического закона. Из многих форм такого изображения наиболее широко используются три: а) короткая (8‑клеточная), б) полудлинная (18-клеточная), в) длиннопериодная (32-клеточная).

В вариантах (а) и (б) элементы – лантаноиды и актиноиды вынесены в нижнюю часть таблицы или в отдельные группы.

Физической основой структуры таблицы

---