ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 653
Скачиваний: 4
СОДЕРЖАНИЕ
1. ОПИСАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
2.1. Кинематическая схема механизма
2.2 Выбор электродвигателя, расчет параметров
2.3. Механическая система дополнительного электропривода
2.4 Выбор тиристорного преобразователя, расчет параметров
Необходимое значение полного сопротивления обмотки фазы реактора
2.5 Определение параметров тиристорного преобразователя
2.6 Расчет параметров якорной цепи привода
2.7 Определение области допустимой работы дополнительного
электропривода подъемной лебедки
2.8 Структурная схема силового канала дополнительного
электропривода подъемной лебедки
3. ОПТИМИЗАЦИЯ ЛИНЕАРИЗОВАННОЙ САУ
ДОПОЛНИТЕЛЬНОГО ЭЛЕКТРОПРИВОДА БУРОВОЙ ЛЕБЕДКИ
3.1 Функциональная схема дополнительного электропривода буровой
3.2 Структурная схема САУ электропривода РПД
3.3 Оптимизация контура тока якоря
3.4. Оптимизация контура скорости
3.5. Оптимизация контура положения
4.ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ САУ ДОПОЛНИТЕЛЬНОГО
ЭЛЕКТРОПРИВОДА БУРОВОЙ ЛЕБЕДКИ
4.1 Основные нелинейности САУ дополнительного электропривода
4.2 Структурная схема нелинейной САУ дополнительного
электропривода буровой лебедки
4.3. Имитационная модель нелинейной САУ дополнительного
электропривода буровой лебедки
4.4. Исследование САУ дополнительного электропривода буровой лебедки на имитационной модели
ЗАДАНИЕ ДЛЯ РАЗДЕЛА «ФИНАНСОВЫЙ МЕНЕДЖМЕНТ,
РЕСУРСОЭФФЕКТИВНОСТЬ И РЕСУРСОСБЕРЕЖЕНИЕ»
5 ФИНАНСОВЫЙ МЕНЕДЖМЕНТ, РЕСУРСОЭФФЕКТИВНОСТЬ
5.1 Анализ конкурентных технических решений
5.2 Планирование научно-исследовательских работ
5.3 Определение ресурсоэффективности исследования
ЗАДАНИЕ ДЛЯ РАЗДЕЛА «СОЦИАЛЬНАЯ ОТВЕТСТВЕННОСТЬ»
6.1 Правовые и организационные вопросы обеспечения безопасности
6.2 Производственная безопасность
6.3 Экологическая безопасность
3.3 Оптимизация контура тока якоря
Оптимизацию контура тока осуществляем без учета отрицательной обратной связи по ЭДС двигателя, что соответствует режиму работы с заторможенным двигателем. Структурная схема приведена на рисунке 3.3 ,где пунктирной линией показана неучтенная обратная связь по ЭДС двигателя.
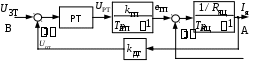
Рисунок 3.3 – Структурная схема контура тока в режиме
заторможенного двигателя.
Контур содержит два инерционных звена первого порядка с постоянными времени Tяц 11,044 10 3 с и Tтп 1,67 10 3 с.
Tяц 11,044 10 3
 Отношение 3 6,61 значительно больше единицы,
Отношение 3 6,61 значительно больше единицы, Tтп 1,67 10
следовательно, принимаем:
-
Tт Tтп 0,00167 с – малая постоянная времени контура; -
Tяц 0,011044 с – большая постоянная контура, которую следует компенсировать.
Контур тока настраиваем на модульный оптимум (МО). С учетом параметров контура выбираем ПИ-регулятор с передаточной функцией
Tрт p 1 1
Wрт p kрт
 kрт
kрт  , Tрт p Tрт p
, Tрт p Tрт pгде Tрт Tяц 0.011044 c – постоянная времени регулятора.
Коэффициент обратной связи по току
 Uзт.макс 10 В
Uзт.макс 10 Вkт 0,0277
 , Iэп.макс 360 А
, Iэп.макс 360 Агде Uзт.макс 10 – максимальное напряжение задания на ток;
Коэффициент усиления регулятора тока
Tяц Rяц 0,01104 0,155008
k
 рт 0,115, kтп kт a Tт т 161,082 0,02777 2 0,00167
рт 0,115, kтп kт a Tт т 161,082 0,02777 2 0,00167 где aт 2 – коэффициент оптимизации контура тока по МО.
Передаточная функция разомкнутого контура тока
1 1
 Wт.раз p
Wт.раз p a Tт т p T
т p 1 2 0,00167 p(0,00167 p 1)
1

5,577 10 6 p2 0,00334 p .
Передаточная функция замкнутого контура тока

Wт.зам p
aт Tт pTт p 11 2 0,00167 p0,00167 p 1
7,198

5,577 106 p2 0,00334 p 1.
По структурной схеме контура тока (см. рисунок 3.3 ) набираем имитационную модель в среде Matlab R2007a, представленную на рисунке. ПИ – регулятор организован по схеме, изображенной на рисунке 3.5.
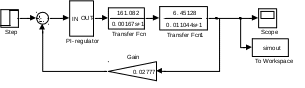
Рисунок 3.4 – Имитационная модель контура тока
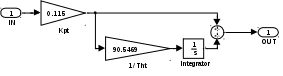
Рисунок 3.5 – Модель ПИ – регулятора в среде Matlab R2006a.
Результаты моделирования переходных процессов в контуре тока, при отработке ступенчатого входного воздействия Uзт 10 В приведены в виде переходной характеристики iя t на рисунке 3.6.
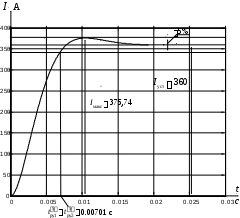
Рисунок 3.6 – Переходная характеристика i t контура тока по структурной
схеме, представленной на рисунке 3.6
По переходной характеристике i t были определены следующие показатели: tру15 0,00701 с – время первого согласования;
tру25 0,00701 с – время переходного процесса;
Iмакс 375,74 А – максимальное значение тока;
Iуст 360 A – установившееся значение тока;
Iмакс Iуст 375,74 360
 100%
100%  100 % 4,37 %– перерегулирование.
100 % 4,37 %– перерегулирование. Iуст 360
Анализ полученных результатов моделирования контура тока, настроенного на модульный оптимум показывает
, что они практически не отличаются друг от друга. Небольшая разница экспериментальных и ожидаемых показателей связана с неточностью обработки графиков. Так как установившаяся ошибка Iуст 0, то в контуре тока обеспечивается астатическое регулирование.
3.4. Оптимизация контура скорости
Структурная схема контура скорости приведена на рисунке 3.7.
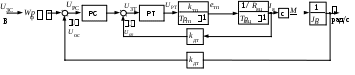
Рисунок 3.7 – Структурная схема контура скорости
Контур тока настраиваем на симметричный оптимум (СО). С учетом параметров контура выбираем ПИ – регулятор с передаточной функцией
Tрс p 1 1
Wрс p kрс
 kрс
kрс  . Tрс p Tрс p
. Tрс p Tрс pМалая постоянная времени контура
Tс aт Tтп 2 0.00167 0.00334 с.
Коэффициент обратной связи по скорости
 Uзс.макс 10 В с
Uзс.макс 10 В сkс 0.0955
 ,
, эп.макс 104.72 рад
где Uзс макс 10 B– максимальное напряжение задания на скорость.
Коэффициент усиления регулятора скорости
k
 рс Jэ kт 1 1,7 0,02777 1 18,418. c k с aс a Tт т 4,018 0.0955 2 2 0,00167
рс Jэ kт 1 1,7 0,02777 1 18,418. c k с aс a Tт т 4,018 0.0955 2 2 0,00167 Большая постоянная времени контура, постоянная времени фильтра
T2 Tрс bс aс aт Tт 2 2 2 0.00167 0.01336 с,
где aс 2, bс 2– коэффициенты оптимизации контура скорости на СО.
Передаточная функция разомкнутого контура скорости, настроенного на
СО
W p с.раз
 b a ac c т Т pт 1
b a ac c т Т pт 1 b a ac c т Т p a a Т p a Т p Т pт c т т т т т 11
2 2 2 0.00167 p 1

2 2 2 0.00167 p2 2 0.00167 p2 0.00167 p0.00167 p 11
0.01336p 1

1 4.977 10 10 p4 2.981 10 7p3 8.925 1 05 p2 .
Передаточная функция замкнутого контура скорости без фильтра на входе