Файл: Сборник задач по дисциплине управленческие решения для студентов дневного отделения, обучающихся по специальностям Менеджмент организации (080507. 65).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 448
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАДАЧА 18. «Оценка согласованности мнений экспертов»
Условие. Результаты ранжирования шести управленческих решений (объектов оценки) пятью экспертами представлены в табл. 4.3.
Требуется оценить согласованность мнений экспертов.
Методические рекомендации по решению. Согласованность оценок экспертов характеризуется двумя показателями: величиной коэффициента конкордации W и наблюдаемым распределением частот (расчетной вероятностью) f2.
Дисперсный коэффициент конкордации W характеризует достоверность итоговой оценки (согласованность мнений экспертов и сходимость результатов); он рассчитывается по формуле:
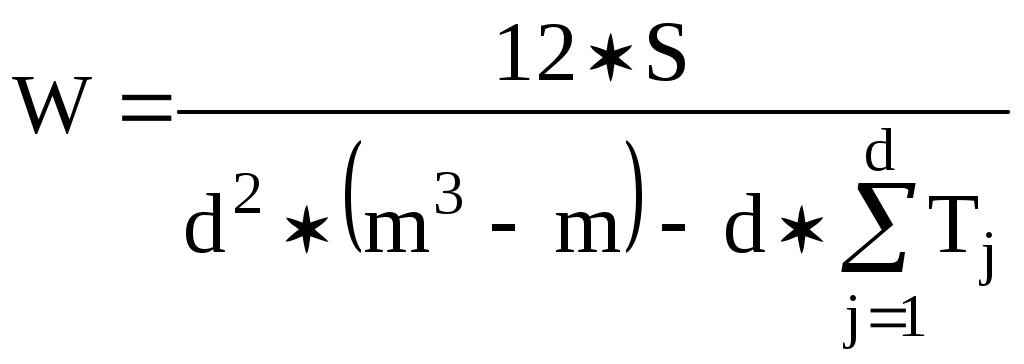 , где (4.1.)
, где (4.1.)S – сумма квадратов отклонений оценок от математического ожидания (среднего значения) суммарного ранга одного объекта:
Таблица 4.3.
Результаты ранжирования m = 6 объектов d = 5 экспертами
(rij - ранг i-го объекта / решения, присвоенный j-м экспертом)
| \ Эксперты Решение(объект)\ | Э1 | Э2 | Э3 | Э4 | Э5 | Итого |
| Y1 | 1 | 2 | 1,5 | 1 | 2 | 7,5 |
| r11 | r12 | r13 | r14 | r15 | ||
| Y2 | 2,5 | 2 | 1,5 | 2,5 | 1 | 9,5 |
| r21 | r22 | r23 | r24 | r25 | ||
| Y3 | 2,5 | 2 | 3 | 2,5 | 3 | 13 |
| r31 | r32 | r33 | r34 | r35 | ||
| Y4 | 4 | 5 | 4,5 | 4,5 | 4 | 22 |
| r41 | r42 | r43 | r44 | r45 | ||
| Y5 | 5 | 4 | 4,5 | 4,5 | 5,5 | 23,5 |
| r51 | r52 | r53 | r54 | r55 | ||
| Y6 | 6 | 6 | 6 | 6 | 5,5 | 29.5 |
| r61 | r62 | r63 | r64 | r65 | ||
| Всего / среднее: 105 / 17,5 | ||||||
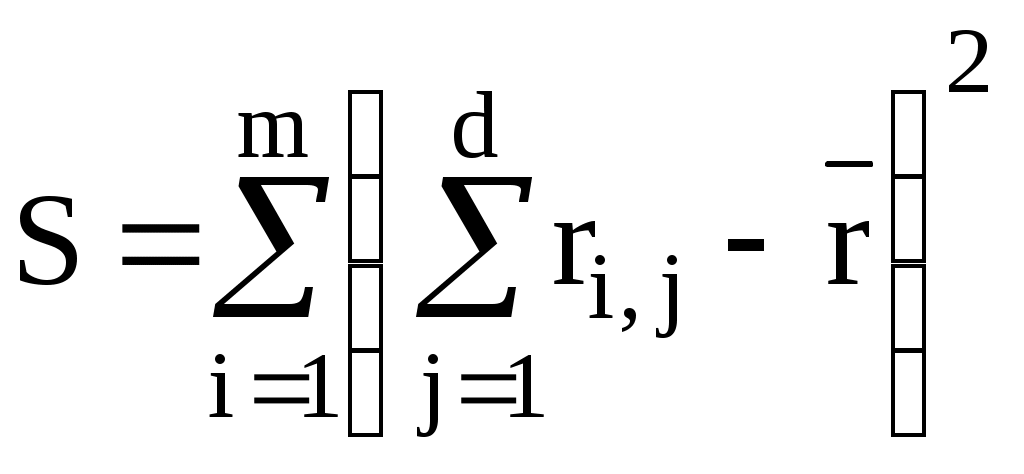 ; (4.2.)
; (4.2.)m - число объектов ранжирования (m = 6);
d - число экспертов (d = 5);
i - индекс объекта;
j - индекс эксперта;
ri,j - ранг, присвоенный i-му объекту j-м экспертом (см. табл. 4.3.);
Tj - показатель связанных рангов в ранжировке j-ro эксперта:
k - номер группы связанных (равных) рангов;
Hj - число групп связанных рангов в ранжировке j-ro эксперта;
hk - число равных рангов в k-й группе связанных рангов
Если в ранжировках совпадающих рангов нет, то все Hj = 0; hk = 0 и, следовательно, Tj = 0; в этом случае формула 10.1 принимает вид:
Величина W = 1 характеризует полное совпадение мнений; W = 0 - свидетельствует, что все ранжировки разные.
Показатель наблюдаемого распределения частот f2 применяется для статистической проверки гипотезы согласованности экспертов путем его сравнения с теоретическим (табличным) 2, найденным для принятого уровня значимости. Сравнение на основе «-квадрат-критерия» (2-критерия) позволяет сделать вывод, что если f2 < 2, то гипотезу о согласии экспертов следует отвергнуть.
2 - теоретическое распределение частот получают на основе таблиц в учебниках математической статистики в соответствии с принятым уровнем значимости (5%-й уровень значимости соответствует 95%-му уровню достоверности) и числом степеней свободы = m - 1, определяемым исходя из числа ранжируемых объектов (наблюдений).
f2 - наблюдаемое распределение частот рассчитывается по формуле:
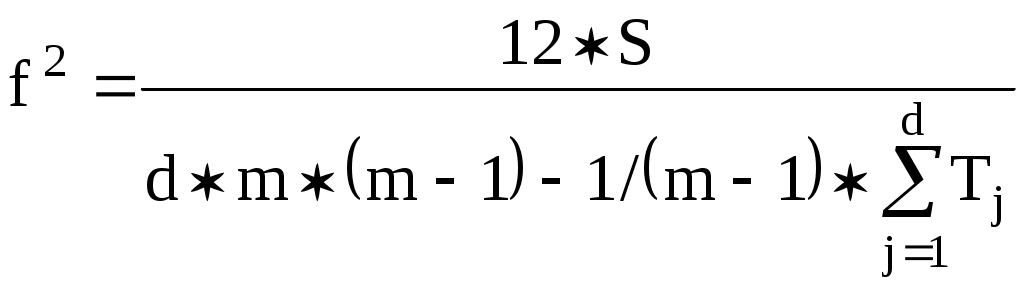 . (4.5.)
. (4.5.)Проведем последовательный расчет значений
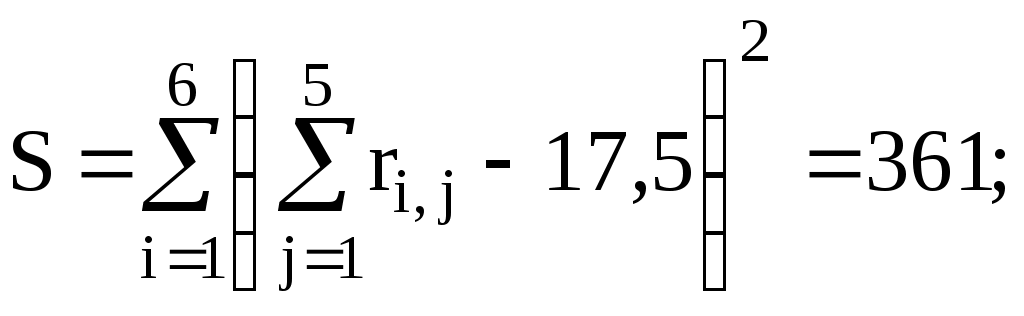
H1 = 1; h1 = 2; T1 = 23 – 2 = 6;
H2 = 1; h1 = 3;, T2 = З3 – 3 = 24;
H3 = 2; h1 = 2; h2 = 2; Т3 = (23 – 2) + (23 – 2) = 12;
H4 = 2; h1 = 2; h2 = 2; T4 = (23 – 2) + (23 – 2) = 12;
H5 = 1; h1 = 2; T5 = 23 – 2 = 6;
Для числа степеней свободы = 6 – 1 = 5 и 5%-го уровня значимости 2 = 11,07 - по таблице.
Поскольку 21,8 > 11,07, то гипотеза о согласии экспертов по ранжировании принимается.
ЗАДАЧА 19. «Групповая оценка объектов»
Условие. Три эксперта (d = 3) оценили значения двух мероприятий (m = 2) решения одной проблемы и дали нормированные оценки этих мероприятий (Х1,j +X2,j = 1) (см. табл. 4.4.).
Таблица 4.4.
Нормированные оценки мероприятий
| Эксперты (Эj) Мероприятия (Yi)\ | Э1 | Э2 | Э3 |
| Y1 | 0,3 | 0,5 | 0,2 |
| X11 | X12 | X13 | |
| Y2 | 0,7 | 0,5 | 0,8 |
| X21 | X22 | X23 |
Требуется дать групповые оценки мероприятий и вычислить коэффициенты компетентности экспертов.
Методические рекомендации по решению. Расчеты осуществляются методом последовательного приближения в итеративном процессе по следующим формулам:
Xi,j - оценки экспертов (см. табл. 11.1);
i - индекс мероприятия;
m - число мероприятий (m = 2);
j - индекс эксперта;
d - число экспертов (d = 3);
t - шаг итерации.
Вычисления начинаются с t = 1
. Начальные значения коэффициентов компетентности принимаются одинаковыми
Первый шаг
X11 = (1/3) * (0,3 + 0,5 + 0,2) = 0,333;
Х21 = (1/3) * (0,7 + 0,5 + 0,8) = 0,667;
1 = 0,333 * (0,3 + 0,5 + 0,2) + 0,667 * (0,7 +0,5 + 0,8) = 1,667;
K11 = (1/1,667) * (0,3 * 0,333 + 0,7 * 0,667) = 0,34;
К21 = (1/1,667) * (0,5 * 0,333 + 0,5 * 0,667) = 0,30;
К31 = (1/1,667) * (0,2 * 0,333 + 0,8 * 0,667) = 0,36.
Второй шаг
X12 = 0,3 * 0,34 + 0,5 * 0,30 + 0,2 * 0,36 = 0,334;
Х22 = 0,7 * 0,34 + 0,5 * 0,30 + 0,8 * 0.36 = 0,676;
2 = 0,324 * (0,3 + 0,5 + 0,2) + 0,676 * (0,7 + 0,5 + 0,8) = 1,676 ;
K12 = (1/1,676) * (0,3 * 0,324 + 0,7 * 0,676) = 0,341;
К22 = (1/1,676) * (0,5 * 0,324 + 0,5 * 0,676) = 0,298;
К32 = (1/1,676) * (0,2 * 0,324 + 0,8 * 0,676) = 0,361.
Третий шаг;
X13 = 0,3 * 0,341 + 0,5 * 0,298 + 0,2 * 0,361 = 0,3235;
Х23 = 0,7 * 0,341 + 0,5 * 0,298 + 0,8 * 0,361 = 0,6765,
3 = 0,3235 * (0,3 + 0,5 + 0,2) + 0,6765 * (0,7 + 0,5 + 0,8) = 1,6765;
K13 = (1/1,6765) * (0,3 * 0,03235 + 0,7 * 0,6765) = 0,341;
К23 = (1/1,6765) * (0,5 * 0,3235 + 0,5 * 0,6765) = 0,298;
К33 = (1/1,6765) * (0,2 * 0,3235 + 0,8 * 0,6765) = 0,361.
Как следует из результатов третьего приближения, вектор коэффициентов компетентности стабилизировался, поэтому дальнейшие вычисления не дают существенного уточнения.
5. Обоснование выбора решения с использованием метода имитационного моделирования
Для решения часто встречающихся задач управления в условиях неопределенности информации в практике управления используют различные методы моделирования: физического, аналогового, математического, имитационного. Все чаще в управлении иногда возникают сложные задачи, решение которых с помощью математических и других моделей не отвечает существу поставленной проблемы. Требуются методы, которые можно использовать в ситуациях, выходящих за рамки системы предпосылок, на которых основаны другие виды моделей.
Имитационное моделирование используется в случаях, когда применение математических аналитических моделей неадекватно или является слишком сложным. Хотя методы имитационного моделирования не слишком элегантны, они являются очень гибкими и мощными в применении. Они шаг за шагом воспроизводят процесс функционирования системы. Эта система может включать ряд стохастических переменных. В системе управления запасами, например, неопределенности могут быть подвержены как ежегодный спрос, так и срок реализации заказа.