Файл: Сборник задач по дисциплине управленческие решения для студентов дневного отделения, обучающихся по специальностям Менеджмент организации (080507. 65).doc

Оба принципа не позволяют учесть интересов всех членов группы. Для их со­блюдения, вводится понятие V - оптимальности, нашедшее отражение в следующих принципах:- принцип Курно. При его реализации все члены группы оцениваются как самостоятельные одноэлементные коалиции. Принцип отражает индивидуальную рациональность, когда ни одному из членов не выгодно менять решение, поскольку не существует лучшего. При этом возможно три типа поведения членов: а) держать­ся вместе, обеспечивая приемлемые условия существования для каждого и сохра­няя статус-кво; б) находиться в условиях конфронтации, думая прежде всего не о собственной выгоде, а о нанесении ущерба противнику (разорение или компромета­ция конкурента, война и т.д.); в) думать только о собственных интересах, т.е. дейст­вовать рационально, не оглядываясь ни на кого, что не всегда приносит ущерб груп­пе;

• 
  принцип Парето. Группа рассматривается как единая коалиция с общей целью и функцией предпочтения. Здесь оптимум один для всех, и смена решений никому не выгодна (тип поведения - статус-кво);
  
• 
  принцип Эджворта - средний между принципами Курно и Парето и наибо­лее общий в жизни. При его реализации возможны все три упомянутых типа поведе­ния.
  

Поскольку последний принцип наиболее распространен, то при групповом ЛПР обычно имеют дело с многокритериальными задачами и сталкиваются с огром­ным числом методов их решения, в различной степени формализованных, в том числе с экспертными оценками, играми с противником и т.д. Поэтому в данном под­разделе, не претендуя на полноту постановок задач и детализацию используемых приемов, рассмотрим только несколько типичных примеров задач по выбору реше­ний групповым ЛПР.

---

ЗАДАЧА 16. «Определение эффективных решений»

Условие. Пусть имеются четыре допустимые решения, и групповое ЛПР состоит из двух членов с функциями предпочтения Ф₁ и Ф₂, соответственно. Оба ЛПР провели упорядочение решений следующим образом:Ф₁ : ; (4.1.)Ф₂ : φ Y₄В соответствии с этим упорядочением значения функций предпочтения, измененные в рангах, представлены в табл. 4.1. Таблица 4.1.Предпочтения членов группы

Предпочтения\Решения	Yl	Y2	Y 3	Y4
Ф1	3	1	2	4
Ф2	2	3,5	1	3,5

Требуется определить эффективные решения, используя принцип Парето. Методические рекомендации по решению. Задача иллюстрирует, как из множества допустимых (приемлемых, удовлетворяющих ограничениям) решений методом логического анализа осуществляется отбор эффективных недоминирующих решений. Эффективные решения между собой несравнимы, так как нельзя сказать, какое из них предпочтительнее. Эффективные решения составляют «множество Парето», из которого уже иным способом выбирается оптимальное (единственное, наилучшее) с привлечением дополнительной информации (вероятности событий, значимости целей, веса членов группового ЛПР. Общая формула отбора: Y  Y_д  Y_э  Y*, где Y – множество альтернативных решений. Y_д – множество допустимых решений. Y_э – множество эффективных решений, Y* ­­- оптимальное решение.Осуществляя выделенный этап отбора решений, будем сравнивать последовательно пары решений по предпочтительности. Решения Y₁ и Y₂, как это следует из таблицы ранжировок, между собой несравнимы, так как мнения группы по их приоритету разделились. В то же время оба

---

члена группы считают, что решения Y₁ и Y₃ находятся в отношении , поэтому решение Y₁ не может быть эффективным, поскольку есть доминирующее лучшее решение Y₃. Следовательно, решение Y₁ исключается из дальнейшего рассмотрения. Оба члена группы считают, что , поэтому решение Y₄ также является неэффективным. Таким образом, из исходного множества четырех решений остались всего два решения Y₂ и Y₃, которые и будем считать эффективными, не отдавая предпочтения ни одному из членов группы.

Для наглядности процедуры определения эффективных решений представим все решения как точки на плоскости в системе координат Ф₁ и Ф₂. На рис. 4.1 по оси Ф₁ отложены предпочтения первого члена группы, а по оси Ф₂ – предпочтения второго члена группы. Измерения предпочтений проведены в порядковой шкале, в которой нет понятий масштаба и начала отсчета, поэтому точки на осях координат, характеризующие ранги, могут быть расположены неравномерно при соблюдении единственного условия . Эффективные решения Y₂ и Y₃ обведены на рисунке контуром.



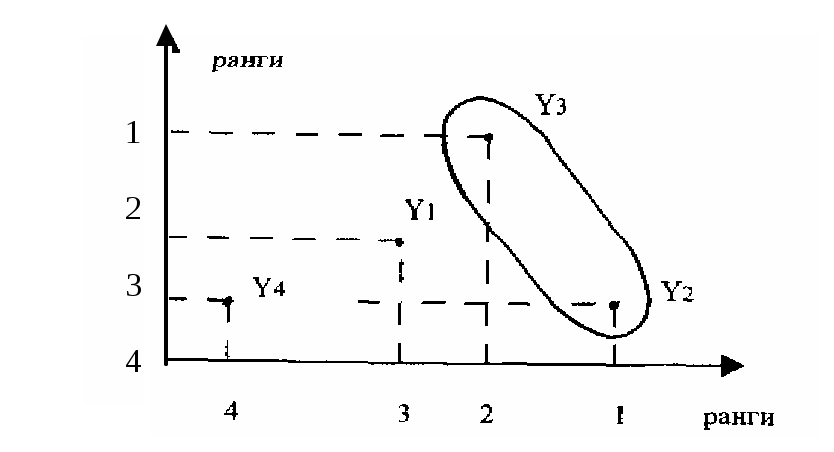
Рис. 4.1. – Графическая оценка предпочтений решений

ЗАДАЧА 17. «Групповой выбор решения при реализации различных принципов и типов поведения членов группы»

Условие. Рассмотрим иллюстративный пример применения принципов группо­вого выбора. Пусть имеется групповое ЛПР, включающее всего два члена. Сформу­лировано два варианта решения проблемы, и каждый из членов группы в соответст­вии со своим предпочтением может выбрать любое решение. Поэтому возможны че­тыре варианта состояний (Y1¹, Y1²), (Y1¹, Y2²), (Y2¹, Y1²), (Y2¹,Y2²), где нижний ин­декс обозначает номер решения, а верхний - номер члена группового ЛПР. Состоя­ние (Y1¹, Y1²) означает, что оба члена выбирают первое решение; соответственно состояние (Y2¹, Y2²

---

) означает выбор членами группового ЛПР второго решения. В состояниях (Y1\ Y2 ), (Y2¹, Y1²) выбираемые членами группы решения не совпада­ют.

Оба члена группового ЛПР высказали свои предпочтения состояний в рангах (см. табл. 4.2).

Таблица 4.2.
Предпочтения состояния для членов группы

Предпочтения\Состояния	Y11, Y12	Y11, Y22	Y21, Y12	Y21,Y22
Ф1	1	3	3	2
Ф2	2	3	3	1

Требуется найти оптимальные решения группового ЛПР для различных прин­ципов группового выбора и типов отношений между членами группы.Методические рекомендации по решению. В условиях гипотезы статус-квои принципа Курнокаждый член группы стремится не ухудшить свое состояние. Поэто­му оптимальными состояниями являются (Y1^1,Y1²) и (Y2¹, Y2²). Это означает, что каждому члену группы выгодно одновременно принять любое решение Y1, либо ре­шение Y2. Действительно, если первый член принял решение Y1¹, то второй член может принять решение Y1² либо Y2².В соответствии с предпочтениями в табл. 4.2., решение Y1² для второго члена предпочтительнее. Аналогично, если первый член принял решение Y2¹, то для вто­рого члена предпочтительным является решение Y2². Соответствующие рассужде­ния можно провести и для первого члена в зависимости от выбора решения вторым членом, чтобы убедиться в том, что оптимальным по принципу Курно в условиях ги­потезы статус-кво является одновременное принятие членами группы решения Y1 или Y2. Состояния (Y1¹ ,Y1²), (Y2¹ ,Y2²) являются состояниями равновесия по прин­ципу Курно.Оптимальным состоянием по принципу Паретов условиях отношения статус-кво также являются (Y1¹, Y1²) и (Y2¹,Y2²). Напомним, что по принципу Парето группа может улучшать свои решения без нанесения ущерба каждому члену, поэтому его применение возможно только при сильной зависимости всех членов группы. Эта за­висимость выражается в общности цели для всех членов группового ЛПР. Действи­тельно, из табл. 4.2. следует, что для выбранных состояний нет доминирующего (т.е. они являются эффективными, но не оптимальными в классическом понимании).

---

Оптимальными состояниями по принципу Эджвортав условиях отношения статус-кво также являются (Y1¹ ,Y1²) и (Y2¹ ,Y2²). Напомним, что по этому принципу каждой коалиции не выгодно менять свое решение, поскольку нет лучшего. Это обобщает принципы Курно и Эджворта в части согласования решений между коали­циями.Таким образом, для всех тех принципов в условиях отношения статус-кво оп­тимальные состояния одинаковы и заключаются в том, что обоим членам группы нужно принимать одинаковое решение, - либо Y1 , либо Y2 .Применение принципов группового выбора дает членам группы информацию о том, что им выгодно держаться вместе, т.е. принимать одинаковое решение, но ка­кое из них, однозначного ответа не дает, оба они - эффективны. Иными словами, гипотеза статус-кво не позволила получить окончательный ответ.В условиях отношения конфронтациидля первого члена группы оптималь­ными решениями будут и Y1, и Y2, поскольку второй член группы на эти решения будет выбирать Y2, и Y1, соответственно. Этим второй член группы будет наносить первому наибольший ущерб (третий ранг - см. табл. 4.2.). Следует заметить, что и первый член группы наносит второму эквивалентный ущерб.В условиях отношения рациональностиоптимальным решением для первого члена является Y1, а для второго - Y2, т.е. члены группы должны принимать разные решения.

---