ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 231
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
Е.А.Рыбакина
НАЧАЛЬНО-КРАЕВЫЕ
ЗАДАЧИ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Министерство образования и науки Российской Федерации
Балтийский государственный технический университет “Военмех”
Е.А.Рыбакина
НАЧАЛЬНО-КРАЕВЫЕ
ЗАДАЧИ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Учебное пособие
Санкт-Петербург
2005
УДК(51:53+517.927.2)(075.8)
Р93
Р
Р93
ыбакина Е.А.
Начально краевые задачи математической физики: учебное пособие / Е.А.Рыбакина; Балт.гос.техн.ун-т. СПб., 2005. 49 с.
Пособие соответствует курсу «Методы математической физики», который читается для специальностей «Приборы и системы лучевой энергетики» и «Триботехника». В нем рассмотрены начально-краевые задачи для дифференциальных уравнений в частных производных, возникающие при изучении различных физических проблем. Излагаются основные методы решения таких задач, дается физическая интерпретация решений. Теоретические сведения сопровождаются упражнениями, в конце пособия приведены задачи для самостоятельного решения.
Предназначено для студентов инженерно-физических специальностей технических вузов.
УДК(51:53+517.927.2)(075.8)
Рецензент: зав.каф. прикладной математики и информатики БГТУ д-р физ.-мат. наук, проф. С.Д.Шапорев
Утверждено
редакционно-издательским
советом университета
© Е.А.Рыбакина, 2005
© БГТУ, 2005
Введение
Современная математическая физика представляет собой довольно обширную научную область. Данный курс лекций в основном ограничивается той ее частью, которая связана с решением дифференциальных уравнений в частных производных, иначе их называют уравнениями математической физики. Различные области физики, описывающие совершенно несхожие по своей физической сущности явления, используют один и тот же математический аппарат – аппарат дифференциальных уравнений в частных производных. Математические вопросы оказываются почти одинаковыми, изучаем ли мы сигнал радара, распространение звуковой волны в жидкости или поле бесспиновых частиц. Таково удивительное свойство природы
, некое математическое единство различных ее проявлений.
Курс уравнений с частными производными существенно отличается от курса обыкновенных дифференциальных уравнений тем, что в нем изучаются далеко не все уравнения, которые можно написать, используя значки
Таким образом, наша цель – рассмотреть основные физические ситуации, выяснить, к каким математическим задачам они приводят, решить эти задачи и исследовать физические следствия полученных решений. Наши рассуждения при этом не всегда будут строгими с точки зрения математика, мы будем оставаться на физическом уровне строгости и только постараемся отмечать пробелы в наших рассуждениях.
В настоящем пособии подробно рассматриваются постановка физических задач и различные методы их решения для случая одномерного пространства, когда независимыми переменными в уравнениях являются время t и одна пространственная переменная x. Волновое уравнение в этом случае переходит в уравнение струны. Такое упрощение значительно сокращает математические выкладки и позволяет сосредоточиться на смысловой стороне проблемы.
Для сокращения записи в дальнейшем используются следующие аббревиатуры: ДУ – дифференциальное уравнение, ОДУ – обыкновенное дифференциальное уравнение, НКЗ – начально-краевая задача, КЗ – краевая задача, НУ – начальные условия, ГУ – граничные условия, с/ф – собственные функции, с/з – собственные значения. Частные производные, как правило, обозначаются нижними индексами, например:
В тексте пособия содержатся упражнения, выполнение которых обязательно для понимания темы. В заключительной части помещены задачи для практических занятий и самостоятельного решения.
Пособие предназначено для студентов III курса, владеющих аппаратом дифференциального и интегрального исчисления, обыкновенными дифференциальными уравнениями, а также знакомых с курсом общей физики.
§1. Вывод уравнения колебаний струны, постановка задач
В
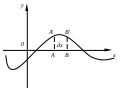
ывод уравнения. Струна – гибкая тонкая нить или проволока (струна фортепиано, скрипки, арфы). Будем считать, что она находится под действием сильного натяжения T0 и в состоянии равновесия без внешнего воздействия вытянута вдоль оси x. Если вывести струну из положения равновесия или подвергнуть действию внешней силы, она начнет колебаться, произвольная точка A в момент t займет положение
Рис.1
Обозначим через
Ускорение выделенного кусочка utt, его масса
. (1)
М

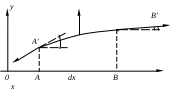
ы получили уравнение малых вынужденных поперечных колебаний струны в общем случае. Уравнение (1) – линейное неоднородное ДУ второго порядка с переменными коэффициентами.
Рис.2
Если струна однородна,
Именно его обычно называют уравнением вынужденных колебаний струны. При отсутствии внешнего воздействия, f(x,t)=0, приходим к уравнению свободных колебаний струны (однородному ДУ):
При выводе (2) мы предполагали, что внешняя сила распределена вдоль струны непрерывно; иногда приходится иметь дело с силой P(t), сосредоточенной в некоторой точке C (рис. 3). Второй закон Ньютона для элемента струны dx, содержащего точку C, имеет вид
причем левая часть равенства стремится к нулю при бесконечном уменьшении dx. Обозначив пределы
Р
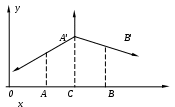
ис.3
Видно, что непрерывная функция u(x,t) имеет в точке Cугловую точку, т.е. скачок производной.
Замечание. При выводе уравнений колебаний мы пренебрегали сопротивлением воздуха; если его учесть, в уравнениях появится слагаемое с первой производной