ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 234
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
и  жестко закреплены, струна находится в положении равновесия. В начальный момент времени малой окрестности точки
жестко закреплены, струна находится в положении равновесия. В начальный момент времени малой окрестности точки 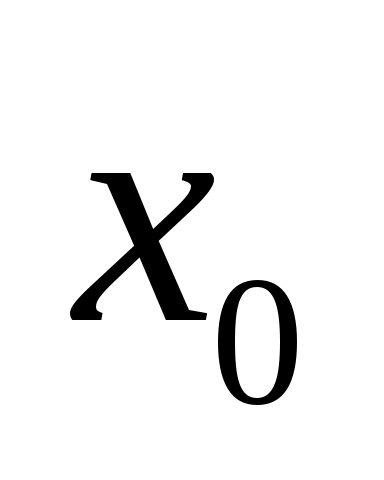 сообщается скорость
сообщается скорость  .
.
Решить эту задачу для случаев, когда оба конца струны свободны и когда один конец закреплен, а другой свободен.
В задачах 20 – 35 решение следует представить в виде ряда Фурье, как это показано в примере 1. В некоторых частных случаях ряд может содержать конечное число слагаемых.
следует представить в виде ряда Фурье, как это показано в примере 1. В некоторых частных случаях ряд может содержать конечное число слагаемых.
Пример 1. Решить I НКЗ для однородного уравнения струны:
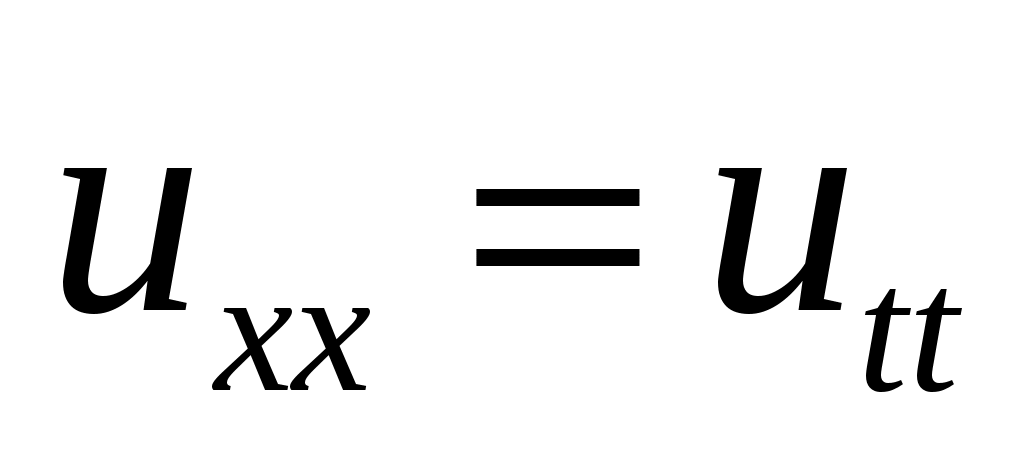 ,
, 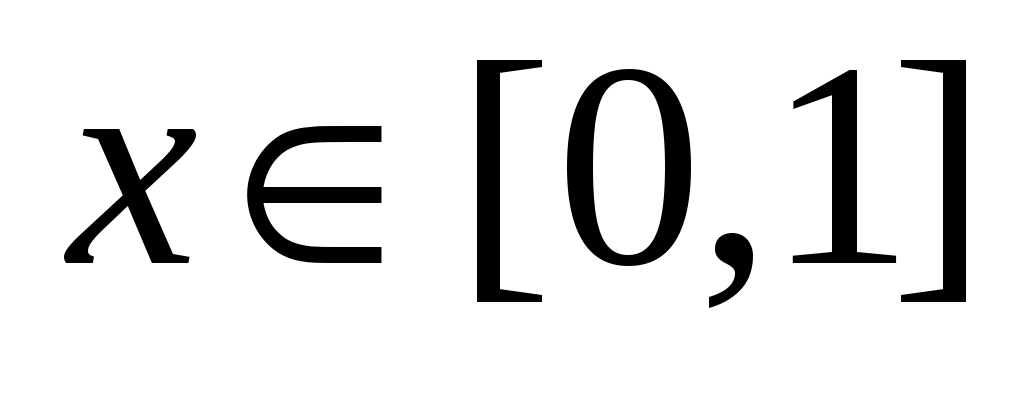 ,
,  ,
,
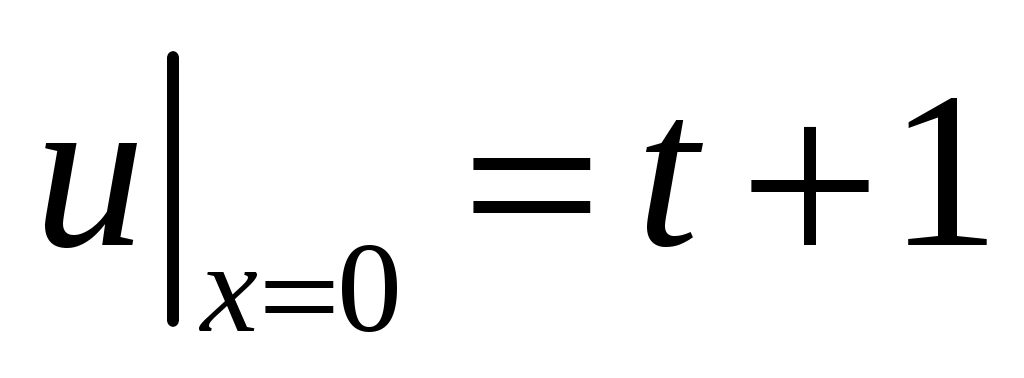 ,
, 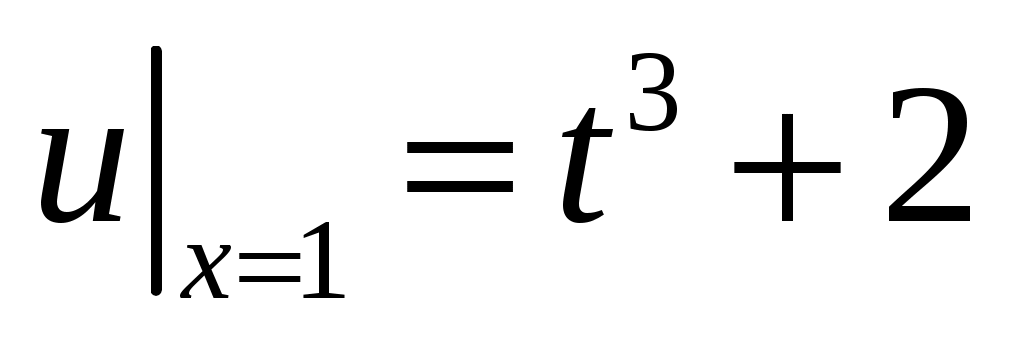 ,
, 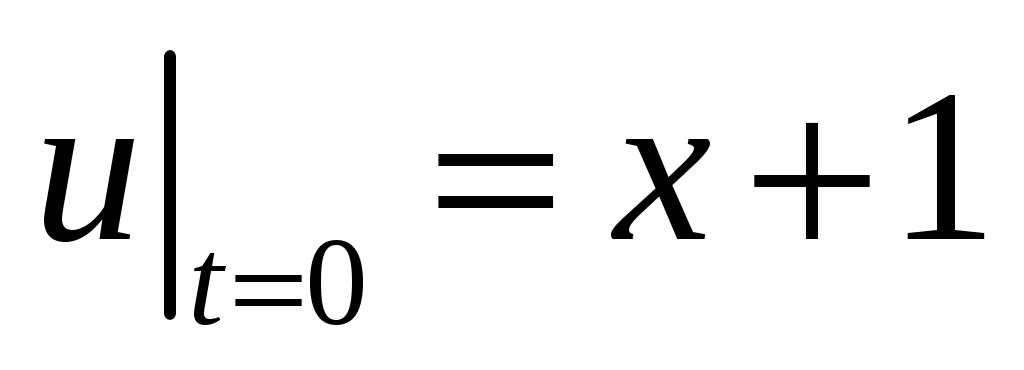 ,
, 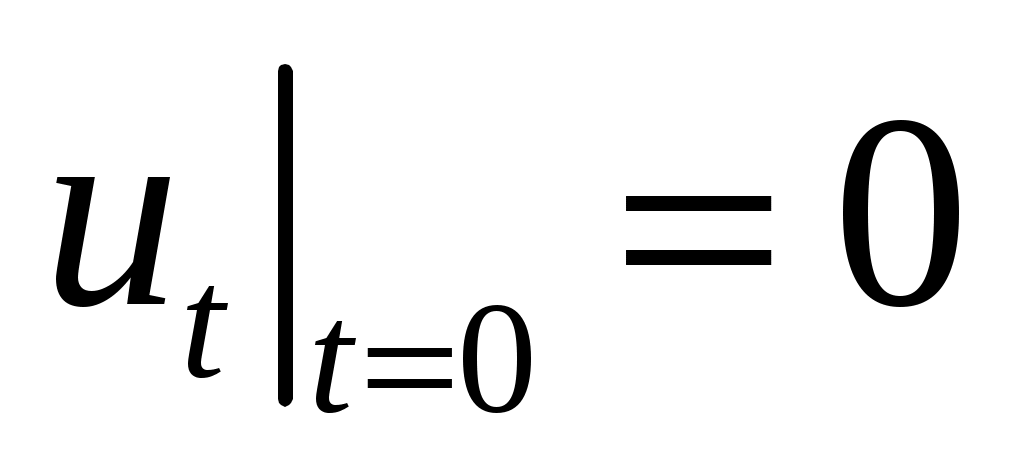 .
.
Решение следует искать в виде суммы (50): , где
, где  - произвольная функция, удовлетворяющая ГУ. Выберем ее линейной по x:
- произвольная функция, удовлетворяющая ГУ. Выберем ее линейной по x: 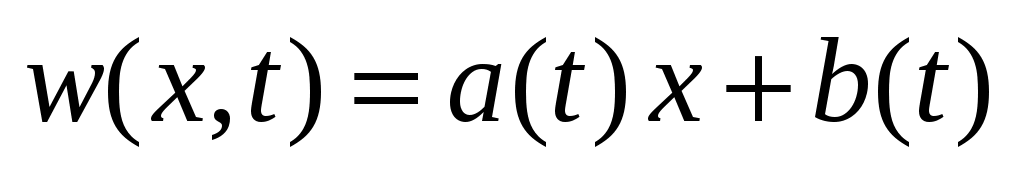 ; подстановка в ГУ дает
; подстановка в ГУ дает
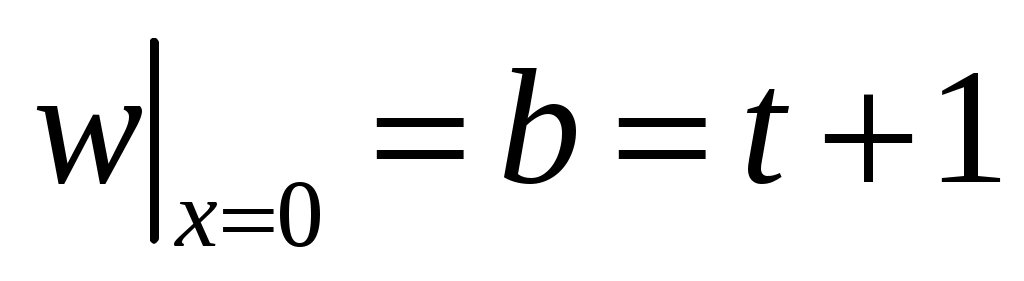 ;
; 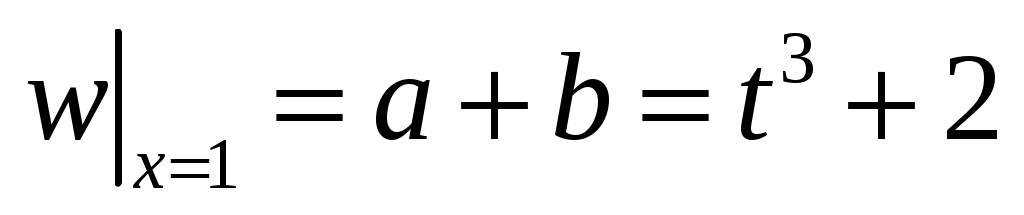 ;
; 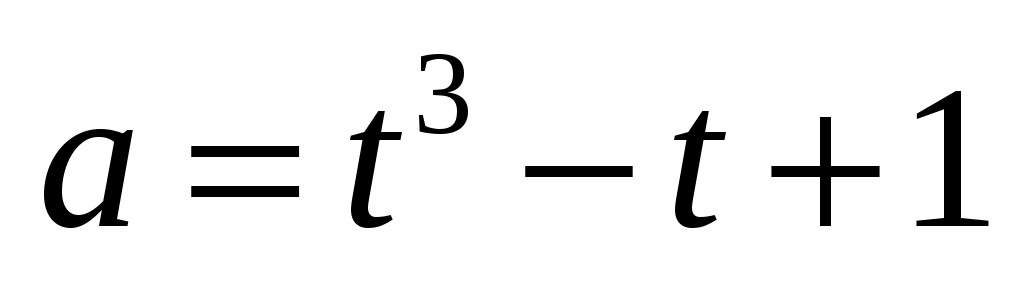 ;
;
окончательно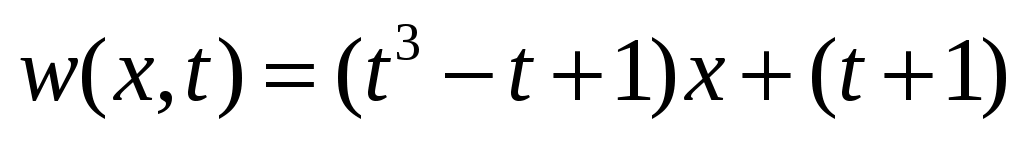 .
.
Подставляя сумму (50) в исходную задачу, получаем НКЗ для функции :
:
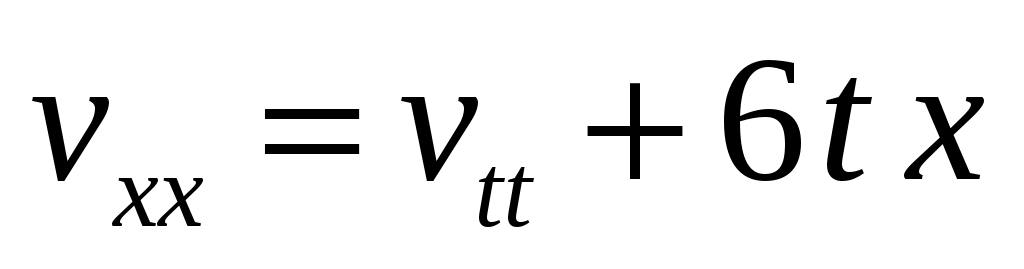
,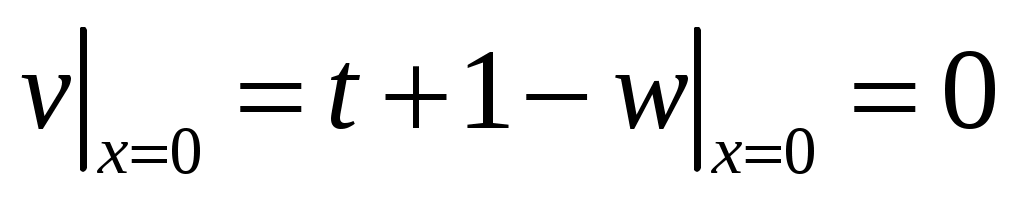 ,
, 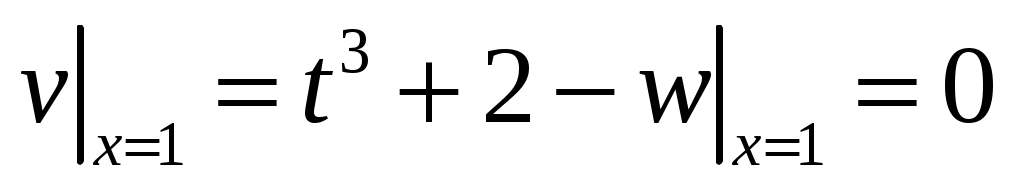 ,
,
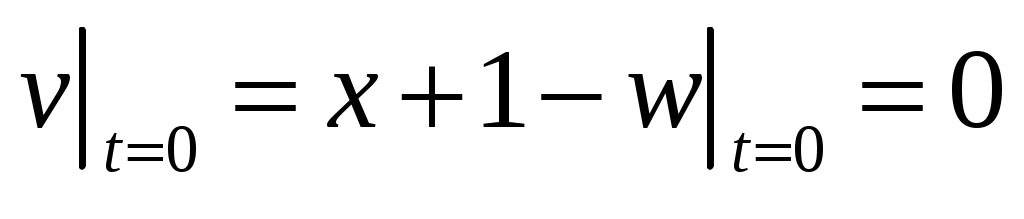 ,
, 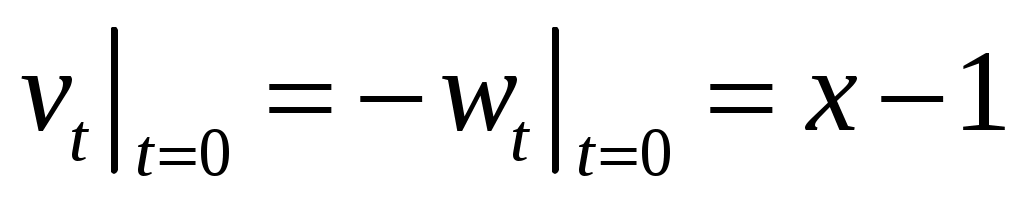 .
.
Видно, что удовлетворяет неоднородному уравнению с нулевыми ГУ и неоднородными НУ. Решение такой задачи построено в § 7, его следует искать в виде суммы
удовлетворяет неоднородному уравнению с нулевыми ГУ и неоднородными НУ. Решение такой задачи построено в § 7, его следует искать в виде суммы 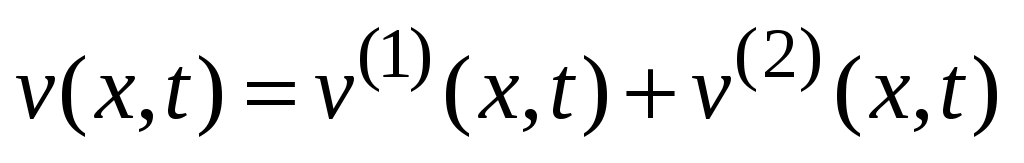 , где
, где 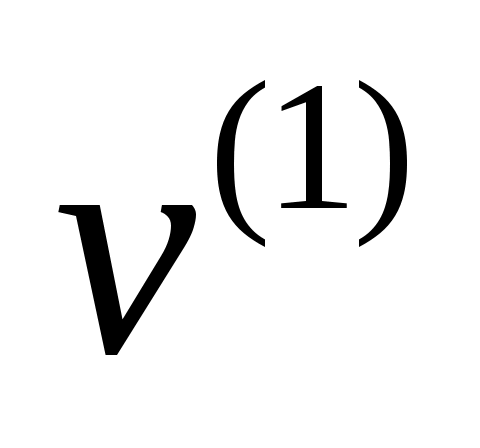 удовлетворяет однородному уравнению с ненулевыми НУ,
удовлетворяет однородному уравнению с ненулевыми НУ, 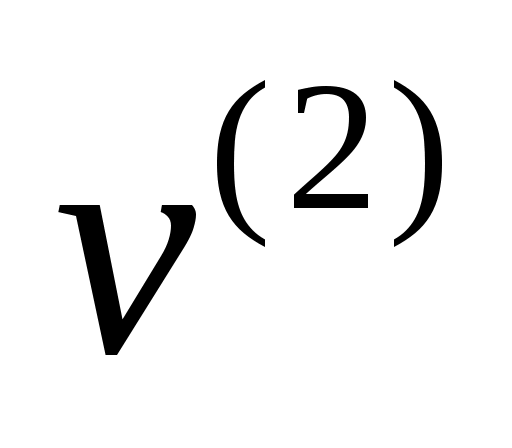 - неоднородному уравнению с нулевыми НУ:
- неоднородному уравнению с нулевыми НУ:
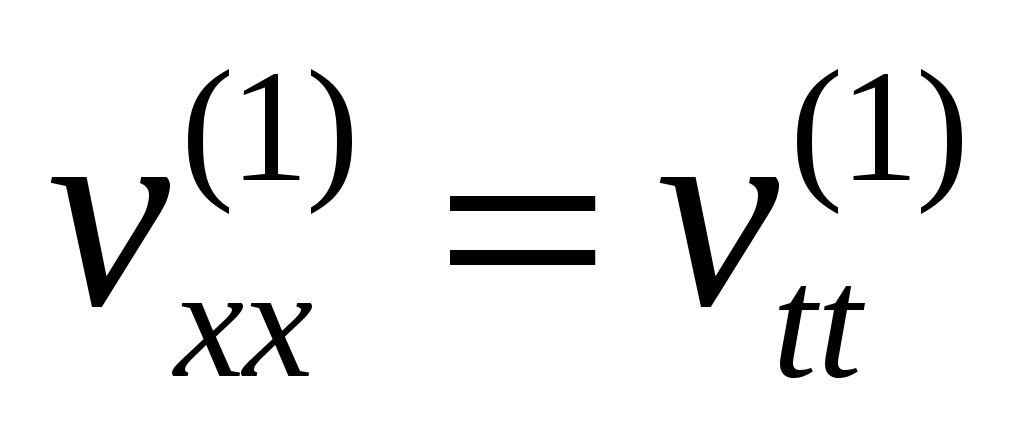 ,
, 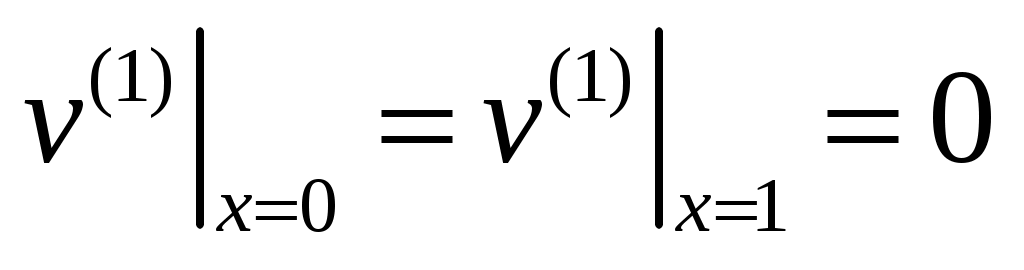 ,
, 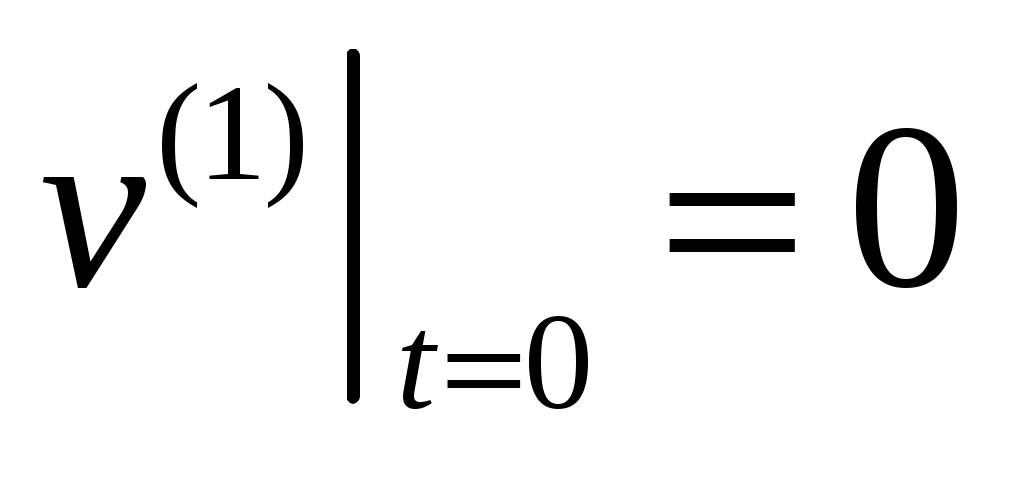 ,
, 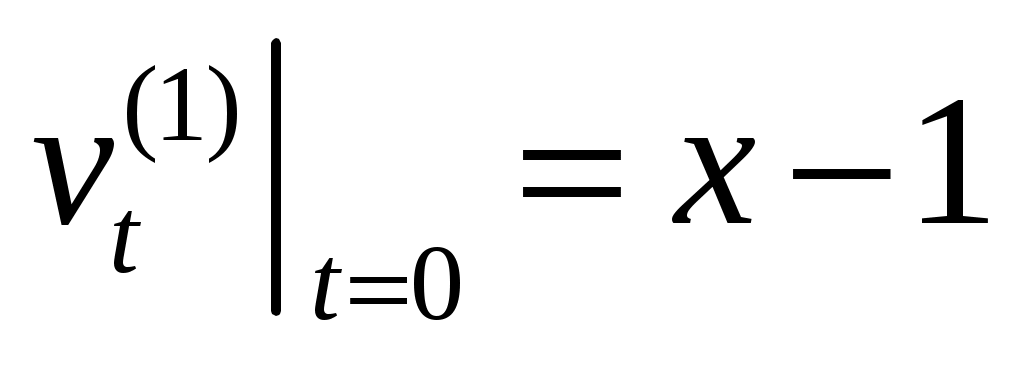 ;
;
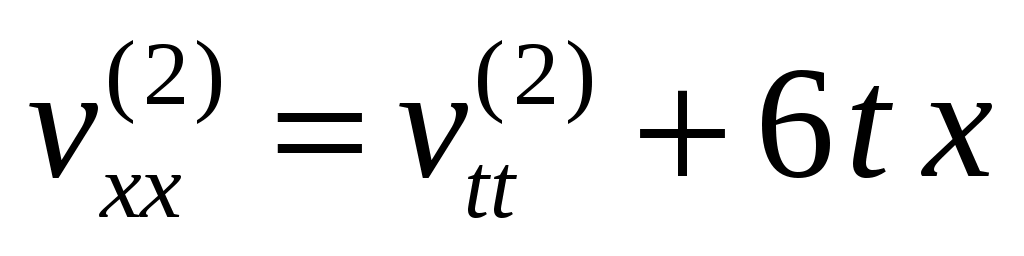 ,
, 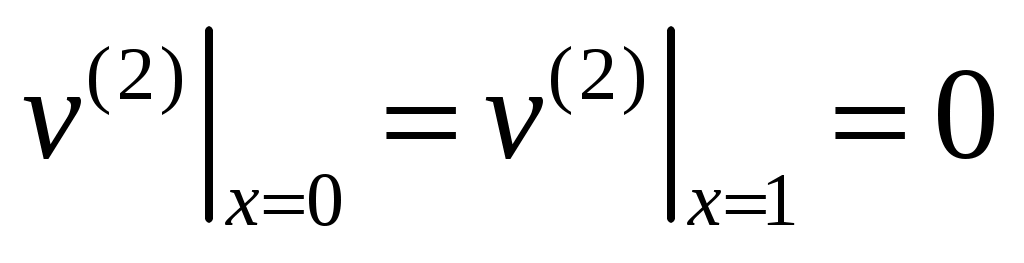 ,
, 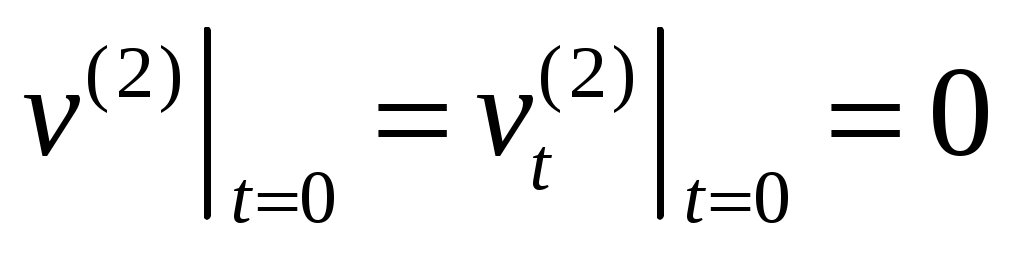 .
.
Обе функции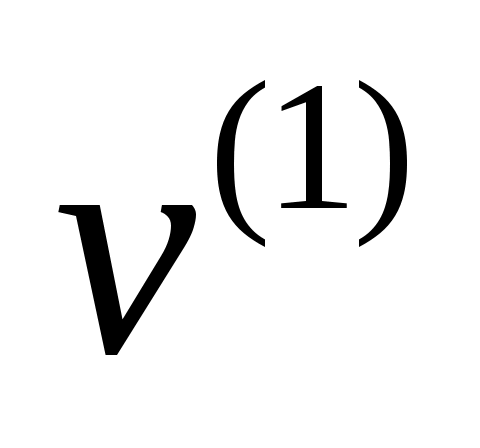 и
и 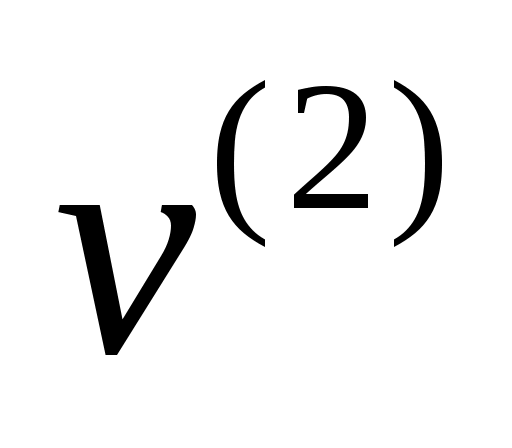 определяются в виде рядов Фурье по
определяются в виде рядов Фурье по 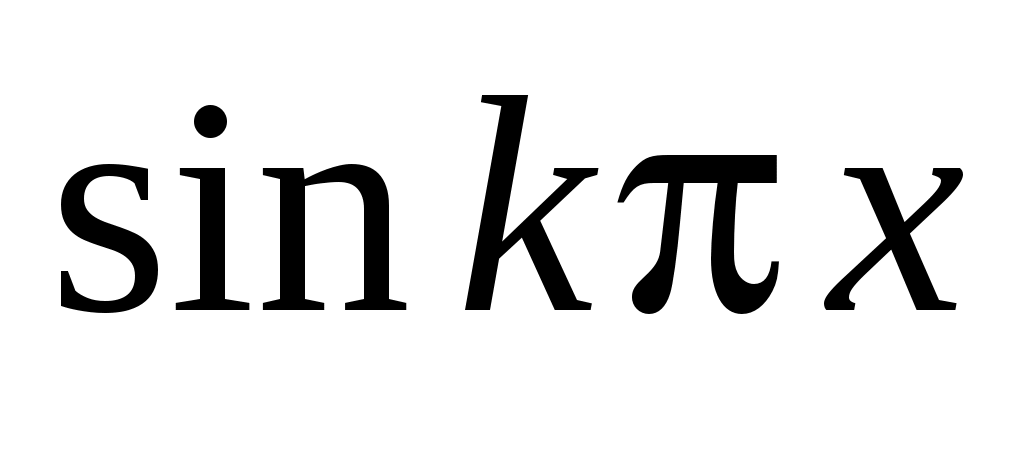 (в нашей задаче
(в нашей задаче 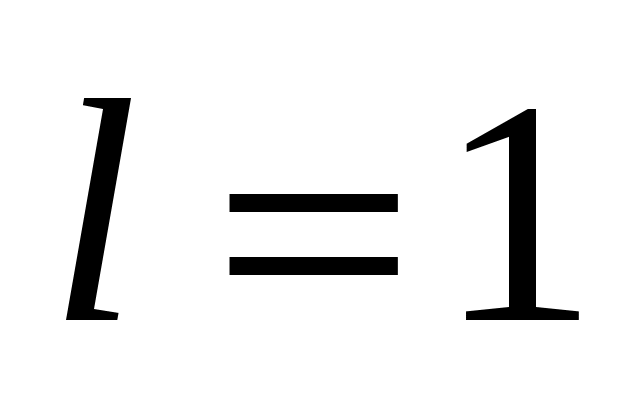 ). Выпишем разложения в ряды Фурье по синусам на промежутке
). Выпишем разложения в ряды Фурье по синусам на промежутке  для входящих в задачу функций:
для входящих в задачу функций:
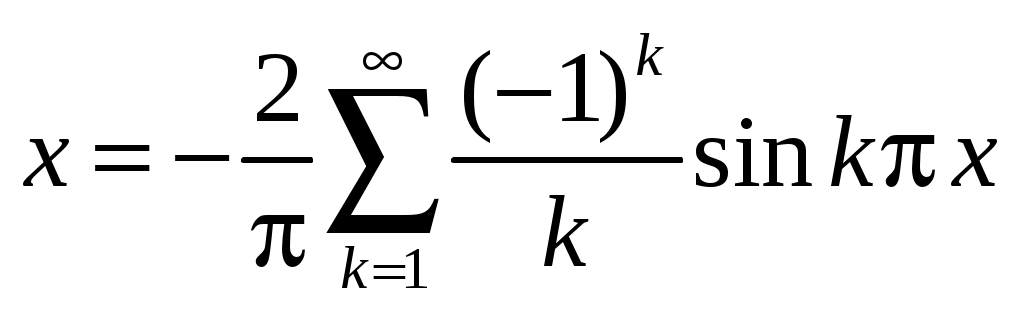 ;
; 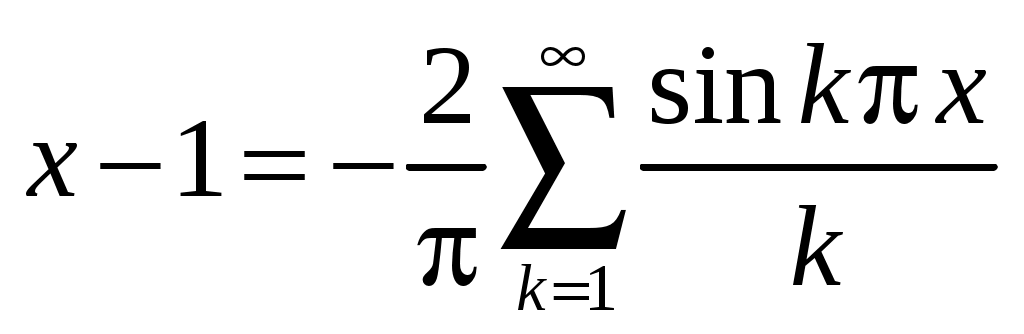 .
.
Ряд Фурье для функции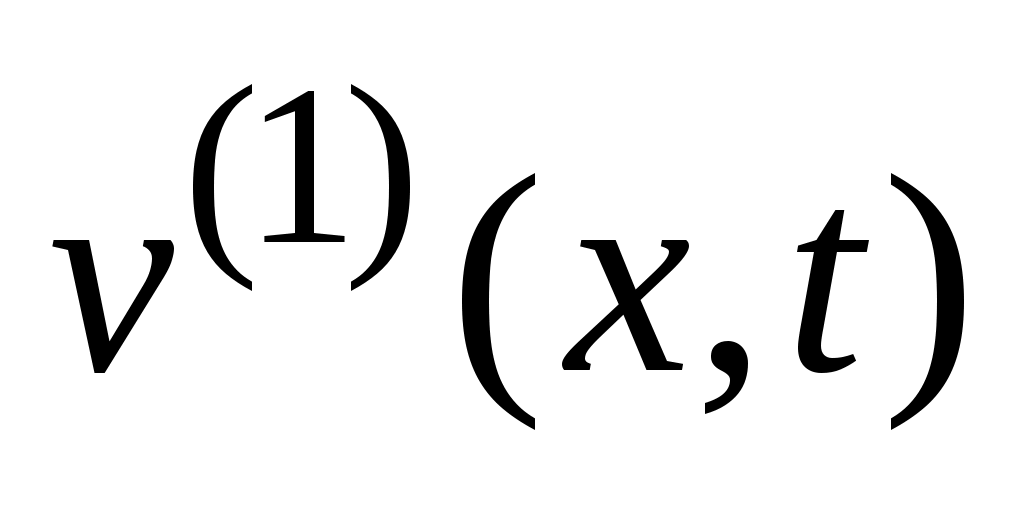 имеет вид (42) (в задаче
имеет вид (42) (в задаче
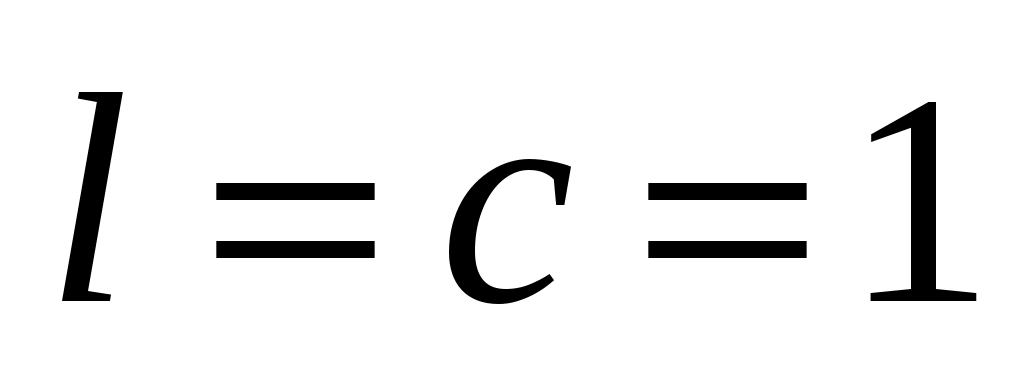 ):
):
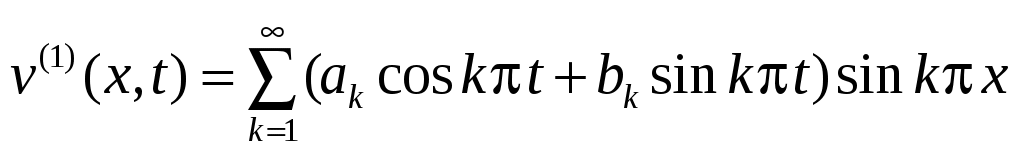 ;
;
подстановка его в начальные условия дает
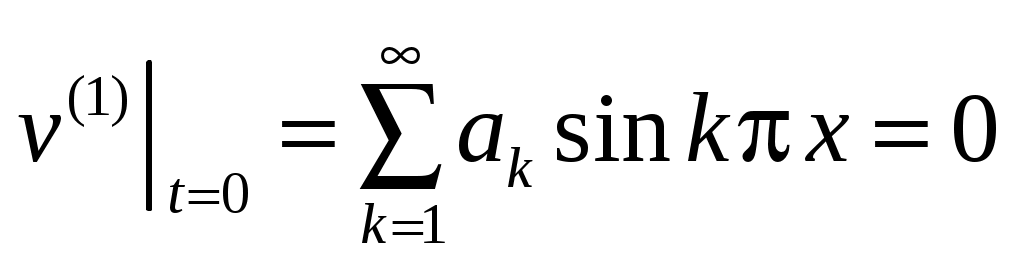 ;
; 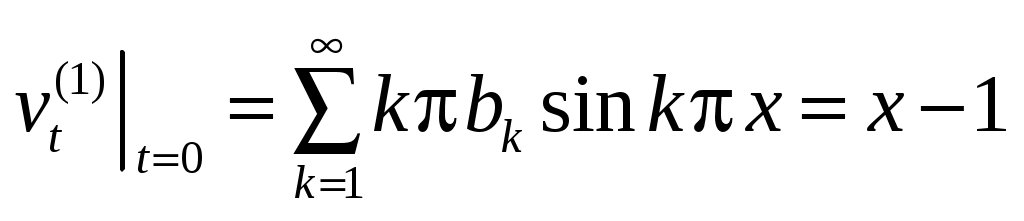 ,
,
следовательно,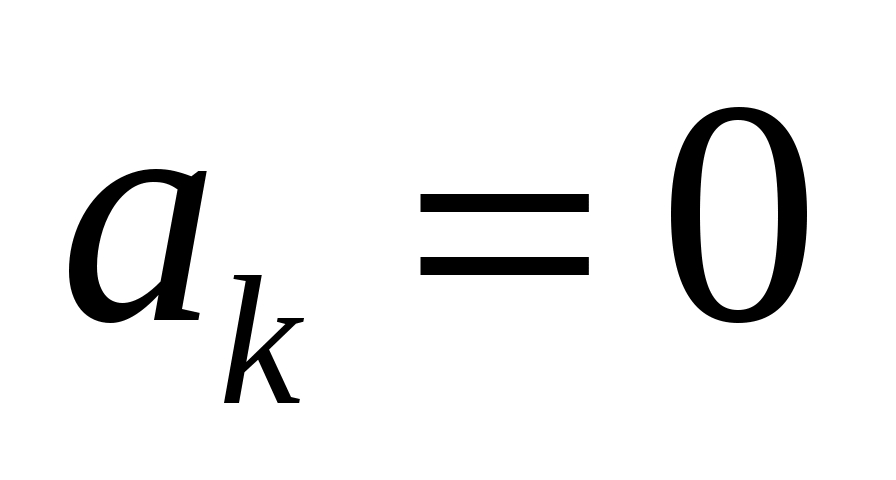 ,
, 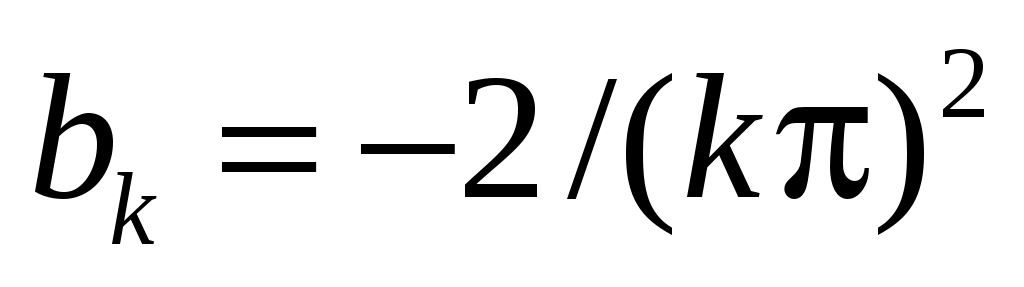 ,
,  .
.
Функция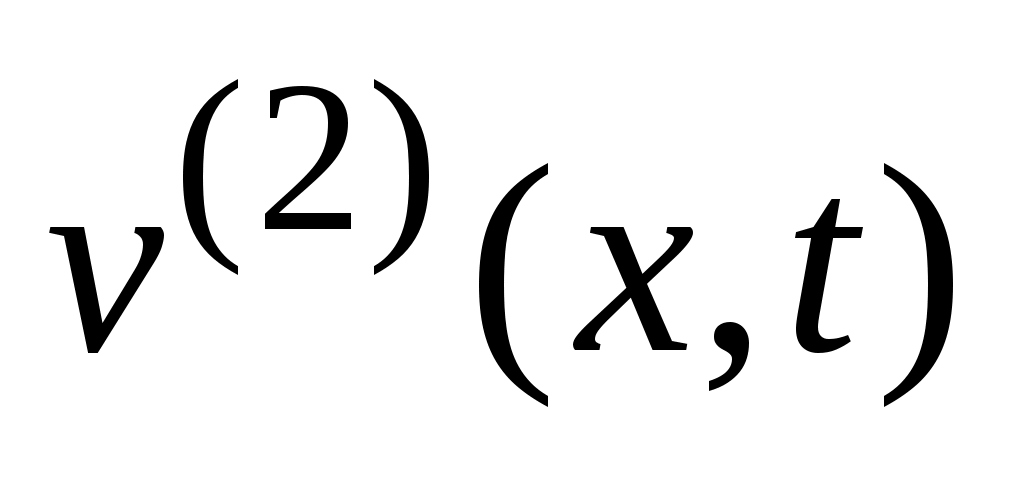 задается рядом (45):
задается рядом (45): 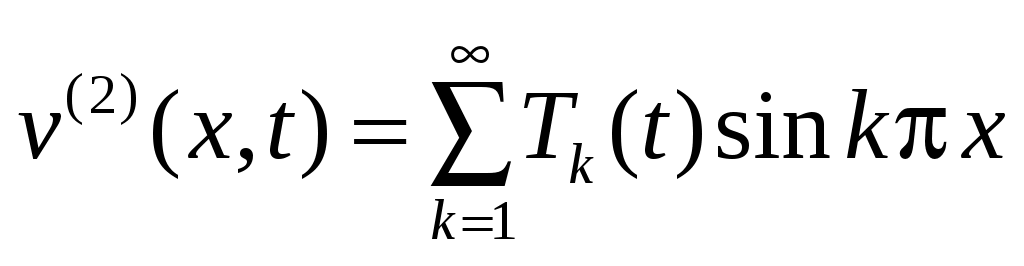 , подставляя его в уравнение и НУ, получаем
, подставляя его в уравнение и НУ, получаем
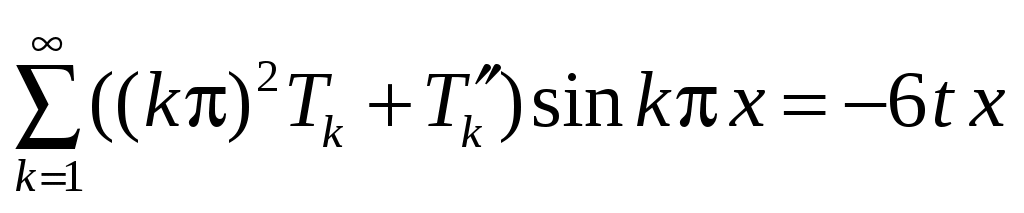 ,
,
следовательно,
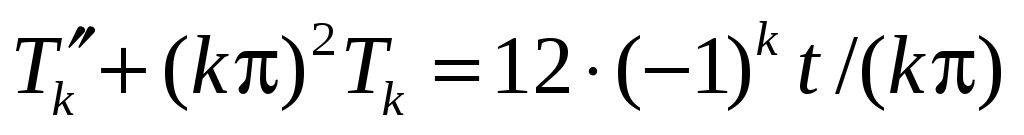 ;
; 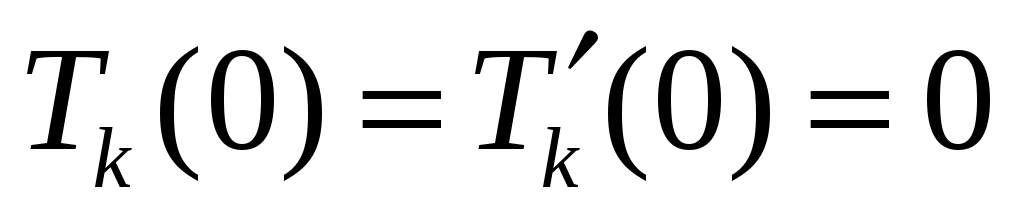 ,
,  .
.
Общее решение этого уравнения
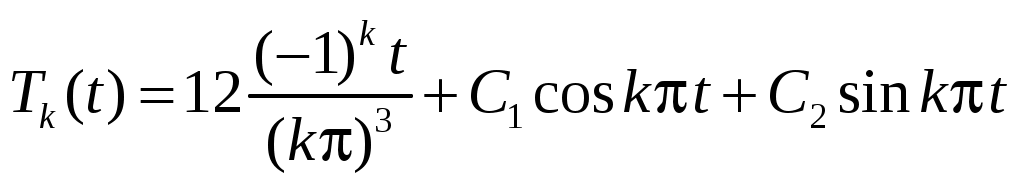 ;
;
из начальных условий следует: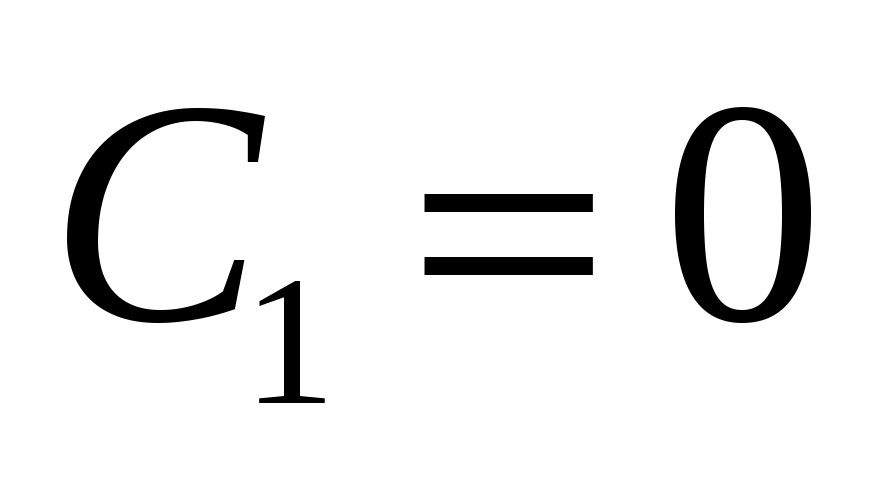 ;
; 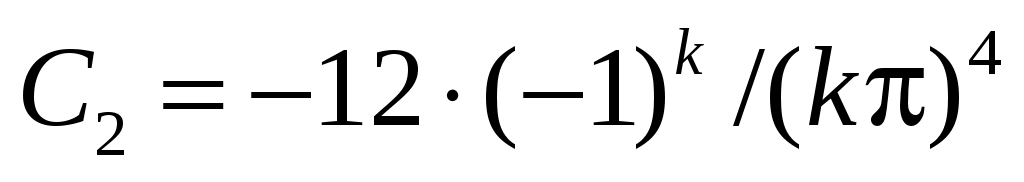
и окончательно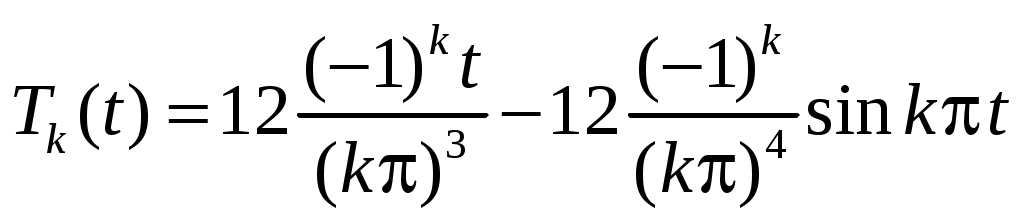 .
.
Таким образом, получены разложения в ряды для решений и
и 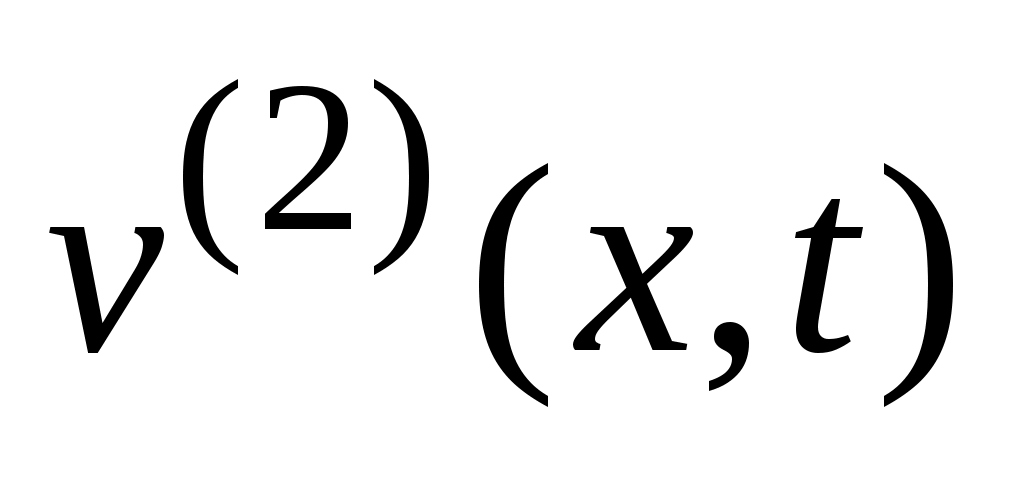 ; суммируя их и
; суммируя их и  , приходим к окончательному ответу:
, приходим к окончательному ответу:
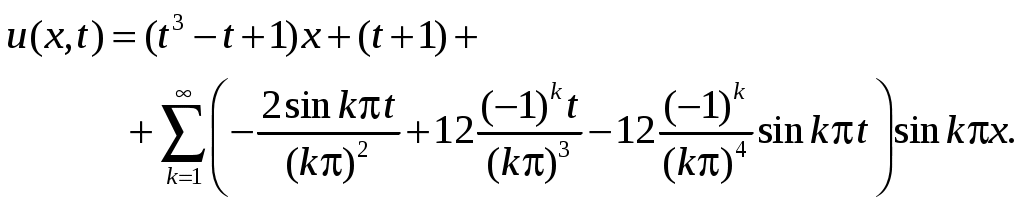
Прямой выкладкой нетрудно проверить, что полученный ряд удовлетворяет всем условиям поставленной задачи.
Пример 2. Решить смешанную НКЗ для неоднородного уравнения:
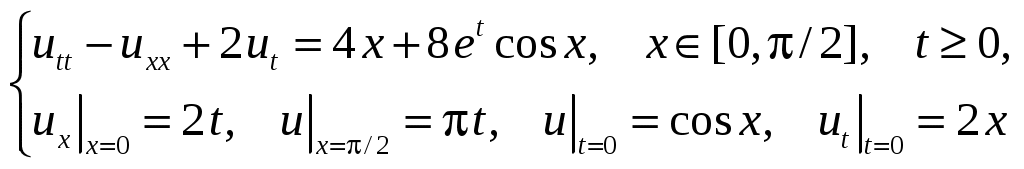
Решение будем искать в виде суммы (50): , где функция
, где функция  удовлетворяет ГУ задачи. Ее можно выбрать линейной:
удовлетворяет ГУ задачи. Ее можно выбрать линейной: 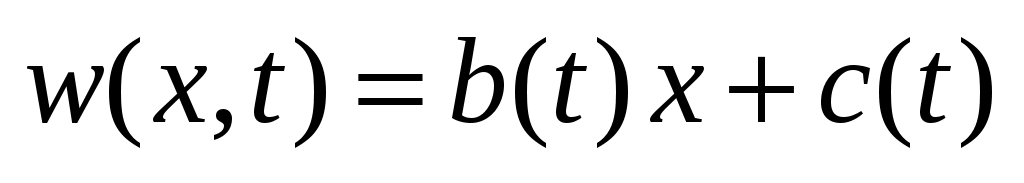 ; подстановка в граничные условия дает равенства
; подстановка в граничные условия дает равенства 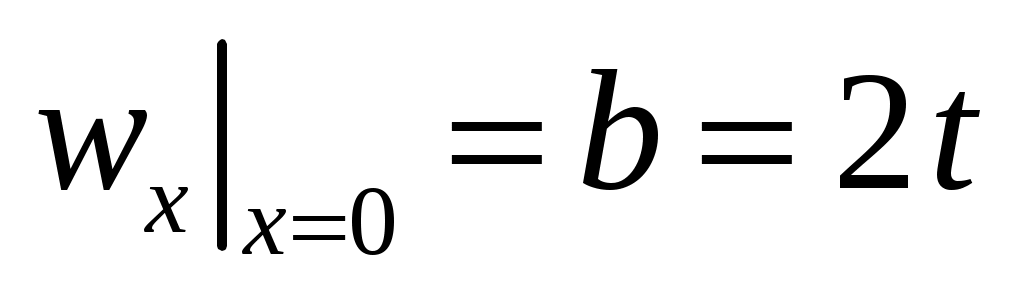 ,
, 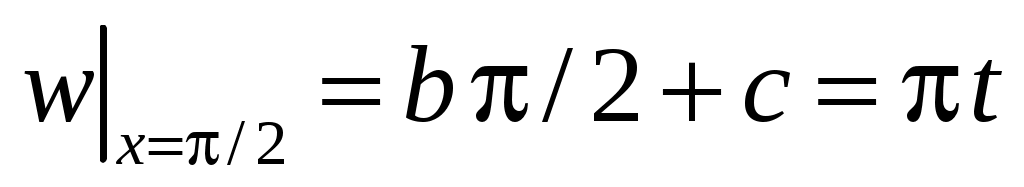 , следовательно,
, следовательно, 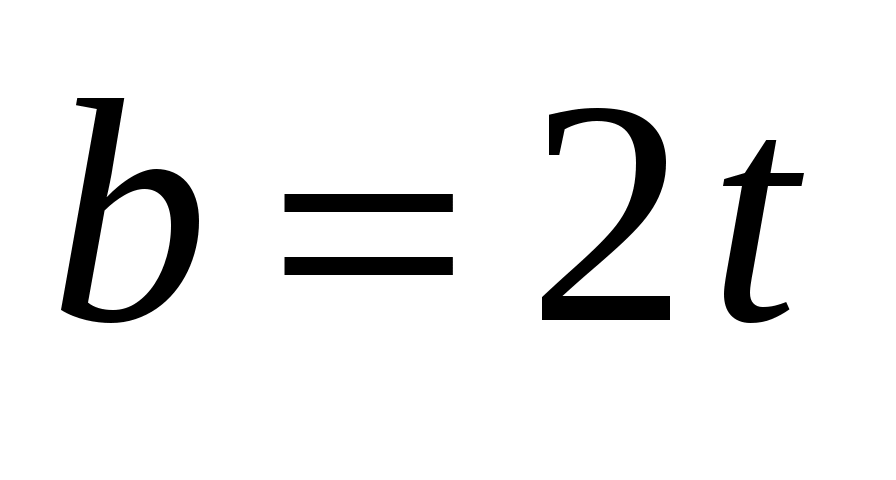 ,
, 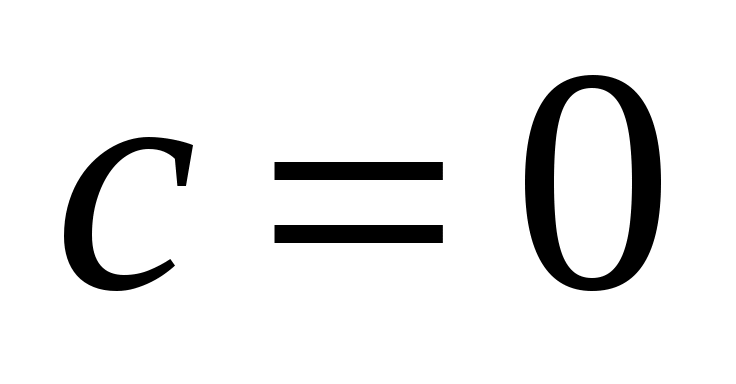 и окончательно получаем
и окончательно получаем  .
.
Для функции возникает следующая НКЗ с нулевыми ГУ:
возникает следующая НКЗ с нулевыми ГУ:
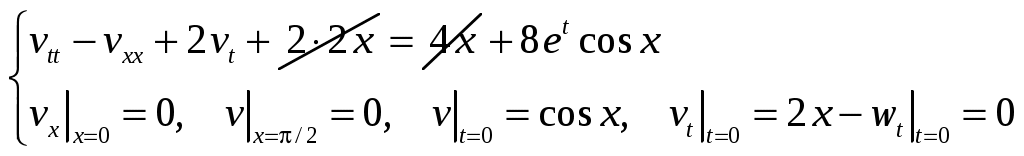
Решение смешанной НКЗ в виде ряда Фурье предлагалось построить в упражнении 12. Повторяя рассуждения § 6, разделим переменные, т.е. будем искать решение соответствующего однородного уравнения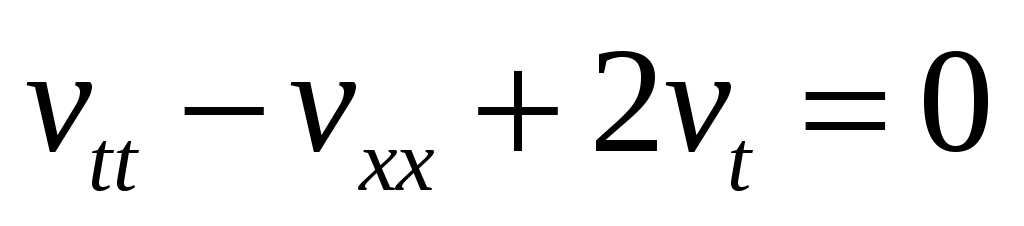 в виде произведения функций (40):
в виде произведения функций (40): 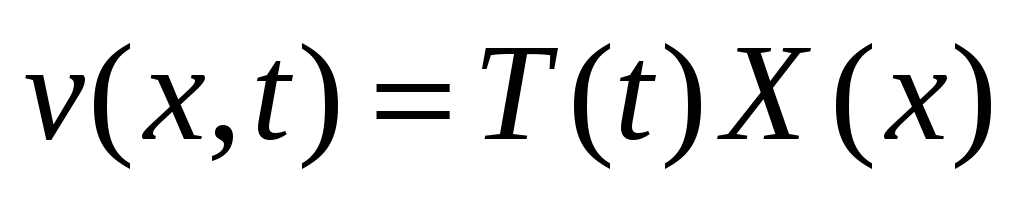 . Подстановка произведения в однородное уравнение приводит к равенству
. Подстановка произведения в однородное уравнение приводит к равенству 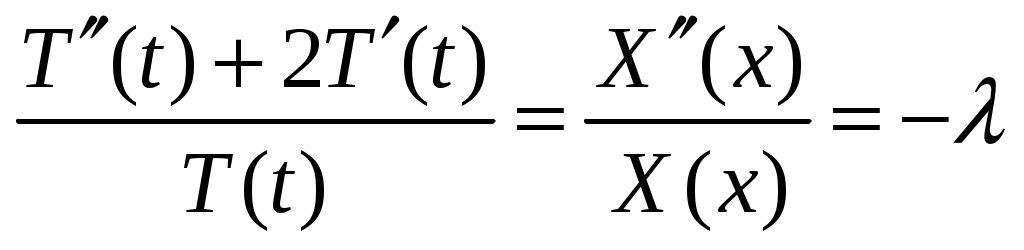 , из которого, с учетом ГУ задачи, выводится следующая КЗ для X(x):
, из которого, с учетом ГУ задачи, выводится следующая КЗ для X(x): 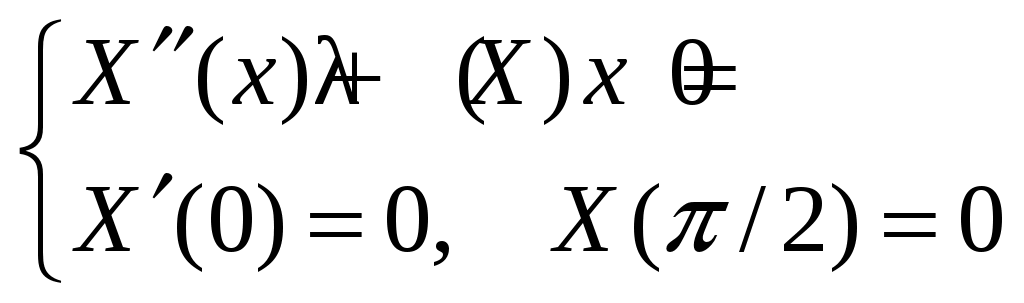 .
.
Нетрудно получить набор собственных функций и собственных значений этой задачи:
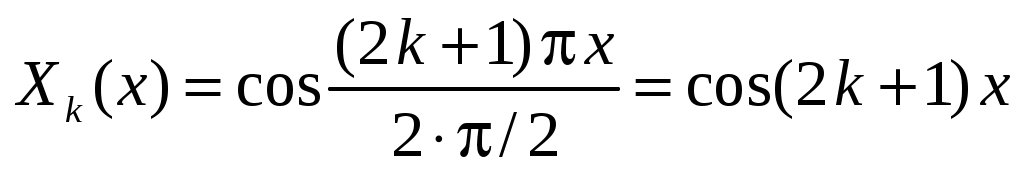 ,
, 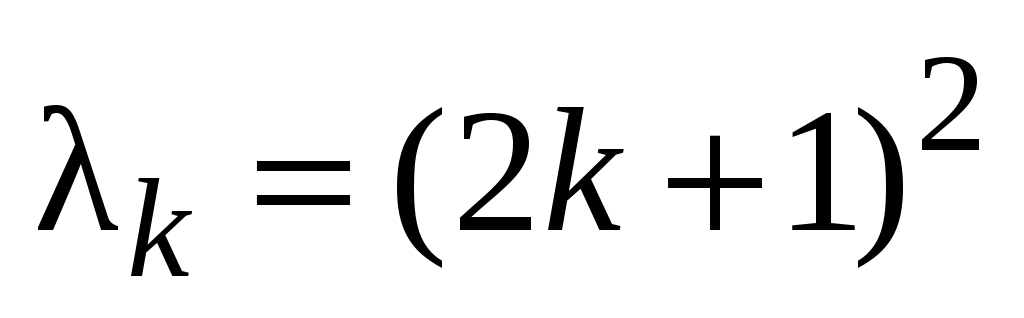 ,
, 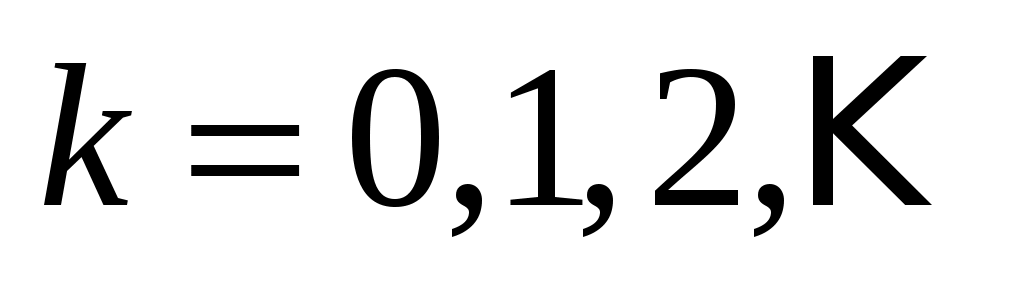 .
.
Решение как однородного, так и неоднородного уравнений следует искать в виде рядов Фурье по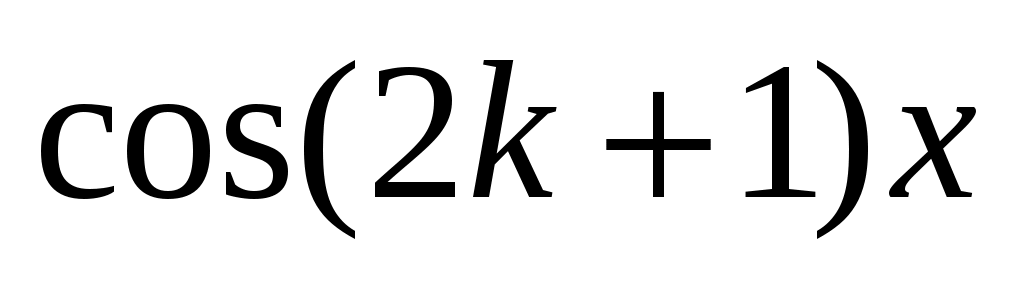
:
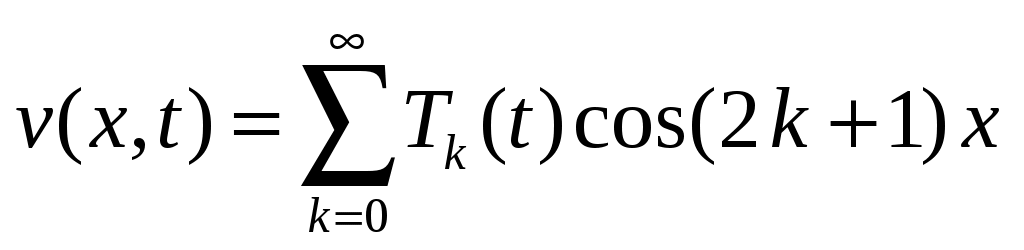 .
.
Подстановка ряда в уравнение и НУ дает равенства
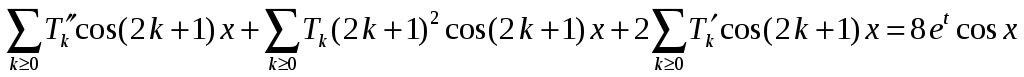
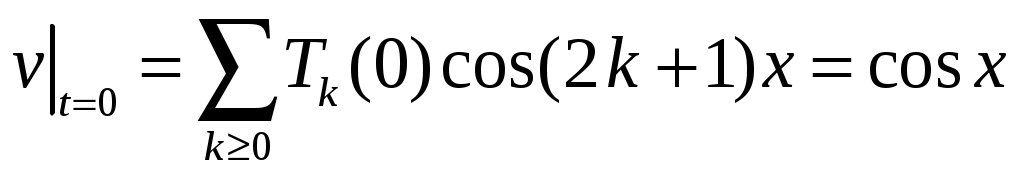 ;
; 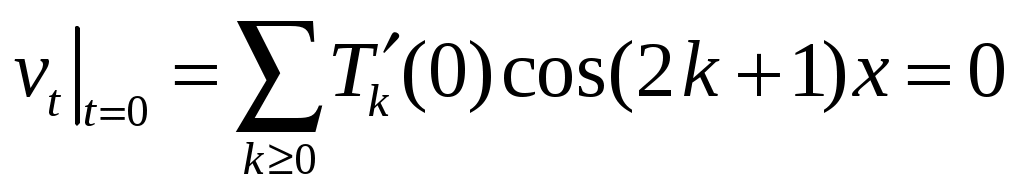 .
.
 является первым членом ряда Фурье по
является первым членом ряда Фурье по  при
при 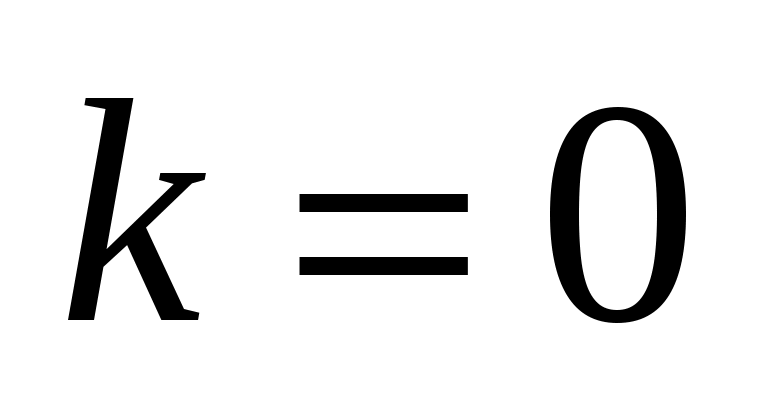 , поэтому, приравнивая коэффициенты Фурье, мы получаем различные задачи для
, поэтому, приравнивая коэффициенты Фурье, мы получаем различные задачи для 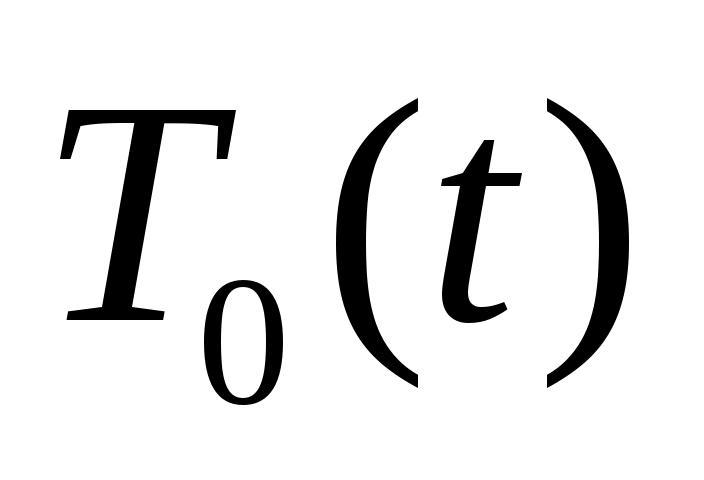 и
и 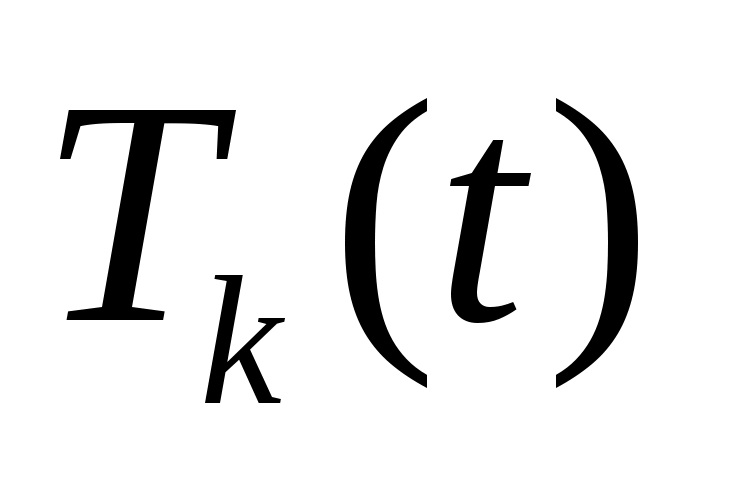 :
:
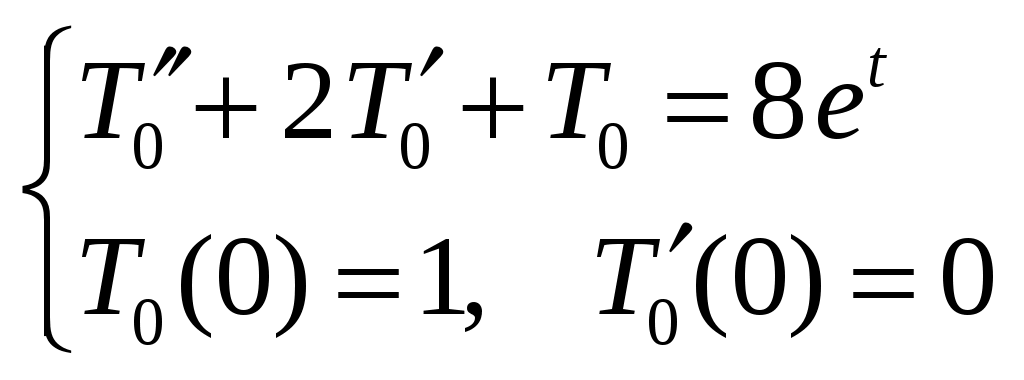 ;
; 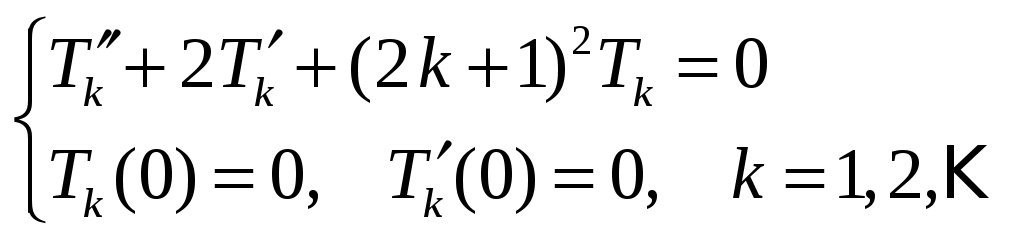
Вторая задача имеет только тривиальное решение: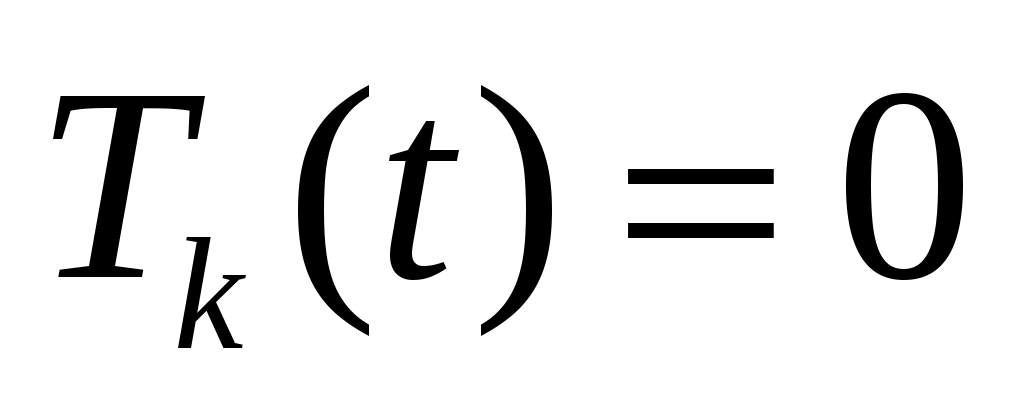 , следовательно, ряд для функции
, следовательно, ряд для функции  состоит из одного первого слагаемого. Общее решение уравнения для
состоит из одного первого слагаемого. Общее решение уравнения для 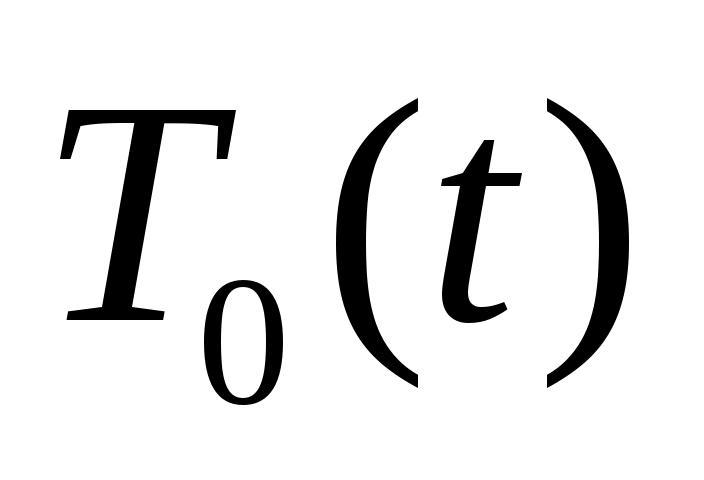 :
: 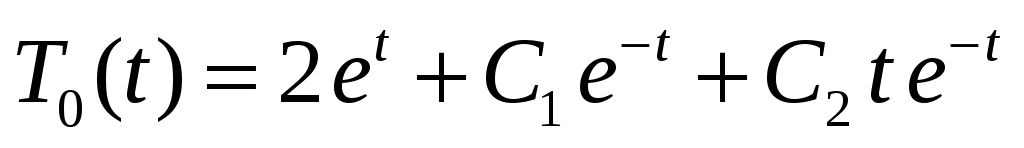 , с учетом НУ получаем
, с учетом НУ получаем
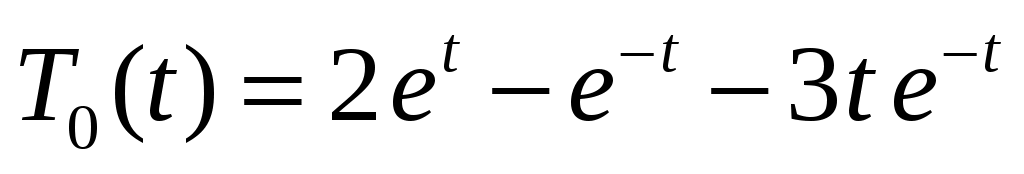 .
.
Для функции имеем
имеем 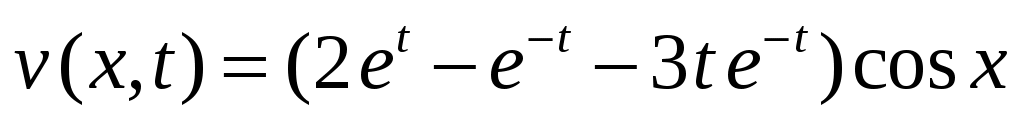 ;
;
ответ исходной задачи:
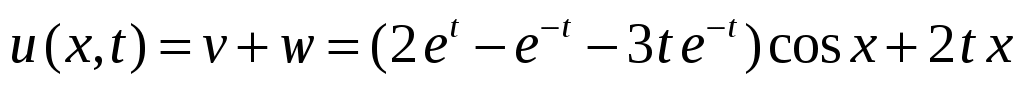 .
.
Решение этой задачи можно было несколько сократить. Установив, что функция представима рядом Фурье по
представима рядом Фурье по  , и заметив, что все входящие в задачу функции содержат только один член
, и заметив, что все входящие в задачу функции содержат только один член 
Решить эту задачу для случаев, когда оба конца струны свободны и когда один конец закреплен, а другой свободен.
Решение начально-краевых задач методом Фурье
В задачах 20 – 35 решение
Пример 1. Решить I НКЗ для однородного уравнения струны:
Решение следует искать в виде суммы (50):
окончательно
Подставляя сумму (50) в исходную задачу, получаем НКЗ для функции
,
Видно, что
Обе функции
Ряд Фурье для функции
подстановка его в начальные условия дает
следовательно,
Функция
следовательно,
Общее решение этого уравнения
из начальных условий следует:
и окончательно
Таким образом, получены разложения в ряды для решений
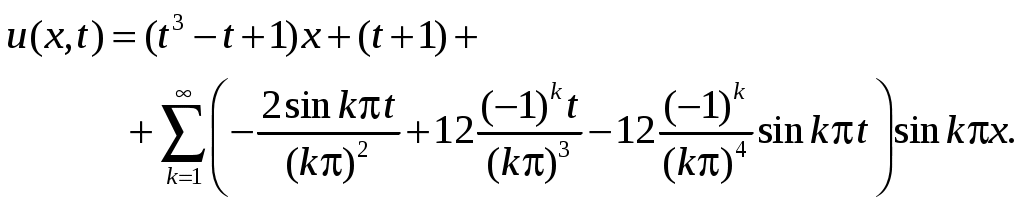
Прямой выкладкой нетрудно проверить, что полученный ряд удовлетворяет всем условиям поставленной задачи.
Пример 2. Решить смешанную НКЗ для неоднородного уравнения:
Решение будем искать в виде суммы (50):
Для функции
Решение смешанной НКЗ в виде ряда Фурье предлагалось построить в упражнении 12. Повторяя рассуждения § 6, разделим переменные, т.е. будем искать решение соответствующего однородного уравнения
Нетрудно получить набор собственных функций и собственных значений этой задачи:
Решение как однородного, так и неоднородного уравнений следует искать в виде рядов Фурье по
:
Подстановка ряда в уравнение и НУ дает равенства
Вторая задача имеет только тривиальное решение:
Для функции
ответ исходной задачи:
Решение этой задачи можно было несколько сократить. Установив, что функция