Файл: Математической физики.doc

, тогда . Если наблюдатель вышел в момент t = 0 из точки x₀ и передвигается вдоль оси x направо со скоростью c, его координата меняется по закону . Для такого наблюдателя смещение струны остается постоянным. Следовательно, первое слагаемое описывает возмущение, которое движется направо со скоростью c, не меняя свою форму, так называемую прямую волну (рис. 5). Второе слагаемое дает обратную волну, которая движется со скоростью c налево. Общее решение уравнения струны возникает при наложении прямой и обратной волн.


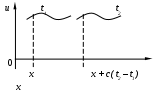
Рис. 5

Решение задачи Коши. Подберем произвольные функции и так, чтобы u(x,t) удовлетворяла НУ задачи (17). Подстановка (18) в НУ дает

.

Продифференцировав первое равенство, находим и . Интегрированием получим

, .

Поскольку , . Подставляя выражения для и в (18), получаем решение Даламбера задачи Коши (17):

---

. (19)

Если функция дважды непрерывно дифференцируема и функция один раз непрерывно дифференцируема на всей вещественной оси, решение u(x,t), задаваемое формулой (19), будет иметь непрерывные первые и вторые производные. Такое решение задачи называется классическим.

Упражнение 4. Проверить прямой подстановкой, что при сформулированных выше условиях на и , формула (19) дает решение задачи Коши (17), т.е. справедлива теорема существования.

Замечание. Поскольку всякое решение задачи Коши, если оно существует, представимо в виде (19), справедлива теорема единственности.

В реальных ситуациях начальными данными могут оказаться функции, не удовлетворяющие указанным требованиям гладкости (например, в начальный момент струна имеет форму ломаной линии). Тем не менее, разумно считать, что формула (19) все равно дает решение задачи (17), хотя u(x,t) и не имеет всюду непрерывные производные до второго порядка. Такое решение называется обобщенным. Теория обобщенных функций и строгое определение обобщенного решения выходят за рамки данного курса.

Физическая интерпретация решения Даламбера

1. Рассмотрим решение в точке в момент времени ; оно зависит от начального смещения в двух точках и и от начальных скоростей на промежутке . Этот интервал вырезается на оси x прямыми , которые называются характеристиками уравнения (3) для точки , рис. 6. Начальные условия на остальной струне на решение в этой точке вообще не влияют. Именно поэтому в пределах некоторого времени можно не учитывать влияние удаленных концов струны на движение ее среднего участка.

---

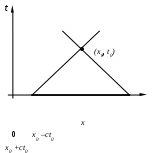
Рис.6
2. Пусть начальные скорости точек струны равны нулю, , струну отклонили и плавно отпустили, тогда

.

Предположим, что начальное возмущение отлично от нуля лишь в конечном промежутке ; проведем через точки и характеристики, в результате полуплоскость (x,t) разобьется на шесть областей (рис. 7). Область I соответствует точкам, до которых в данный момент времени доходят и прямая, и обратная волны; II − только обратная, III – только прямая. До областей IV и V к данному моменту времени возмущение еще не дошло; до точек VI возмущение успело дойти и пройти через них, теперь они покоятся в равновесном положении.

Можно описать эту ситуацию несколько иначе: будем наблюдать за возмущением в некоторой точке . До момента она покоится, после момента возмущение в точке исчезает; и – моменты прохождения переднего и заднего фронтов через точку .

3. Пусть начальные отклонения точек струны равны нулю, , струну толчком вывели из положения равновесия, в этом случае

, где ,

т.е. по-прежнему имеем дело с распространением прямой и обратной волн. Если

---

лишь в конечном промежутке , можно повторить рассуждения предыдущего пункта. Для областей I – V выводы совпадают; в области VI
.







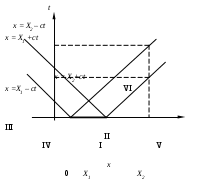
Рис.7
Таким образом, действие начального импульса приводит к тому, что с течением времени точки струны сдвигаются на одинаковый отрезок и после прохождения заднего фронта остаются неподвижными в этом новом положении.

Упражнение 5. Пусть u(x,t) – решение задачи Коши (17). Выберем в качестве начального момент времени и рассмотрим задачу Коши для уравнения (3) с начальными условиями

. (20)

С помощью формулы Даламбера следует показать, что решение задач Коши (17) u(x,t) и (3, 20) совпадают при . Т.е. можно произвольный момент времени выбрать за начальный, взяв в качестве НУ возмущение, достигнутое к этому моменту. Именно это утверждает принцип Гюйгенса^.

Задача Коши для вынужденных колебаний бесконечной струны. Вынужденные колебания бесконечной струны описываются задачей (9):



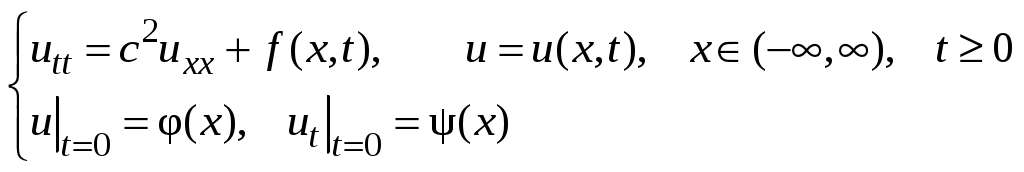
Решение этой задачи можно найти как сумму решений задачи о колебаниях свободной струны (17) и задачи о вынужденных колебаниях струны, в начальный момент невозмущенной:

;

здесь - решение задачи (17), задаваемое формулой Даламбера; определяется задачей

. (21)

Мы могли бы построить сейчас решение (21) в виде интегральной формулы; метод,

---

который при этом используется, будет продемонстрирован в дальнейшем, при решении аналогичной задачи Коши для многомерного волнового уравнения. Там мы вернемся к решению (21), а сейчас объявим результат:

; (22)

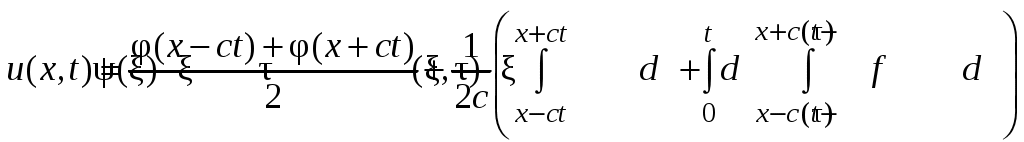(23)

Упражнение 6. Прямой подстановкой проверить, что если дважды непрерывно дифференцируема, и один раз непрерывно дифференцируемы, то функция u(x,t) (23) имеет непрерывные вторые производные и удовлетворяет всем условиям задачи (9), т.е. является ее классическим решением. Таким образом, справедлива теорема существования.

Теорема единственности для задачи (9) очевидна, так как разность двух решений удовлетворяла бы свободному уравнению с нулевыми НУ и тождественно равнялась нулю.

---