ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 228
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
заведомо выполнятся. Ряд (45) написан по аналогии с (42), но функции 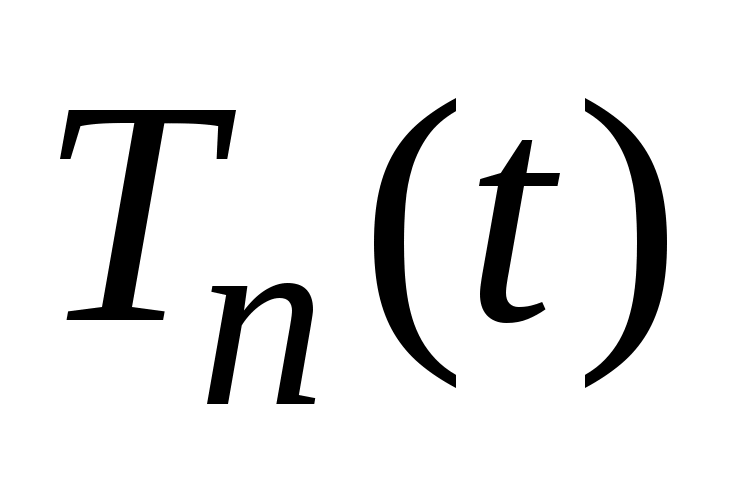 теперь нуждаются в определении.
теперь нуждаются в определении.
Подстановка ряда (45) в уравнение (2) дает
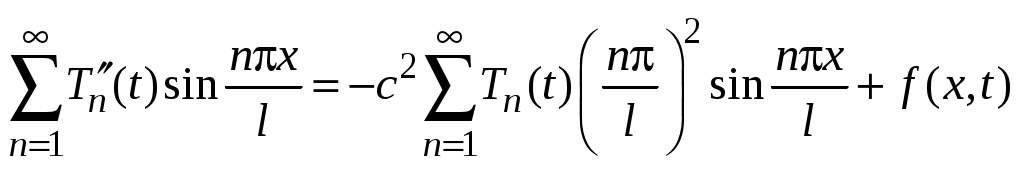 ,
,
следовательно,
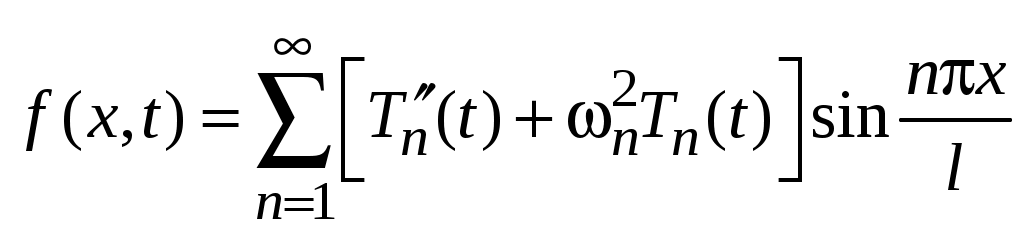 ,
, 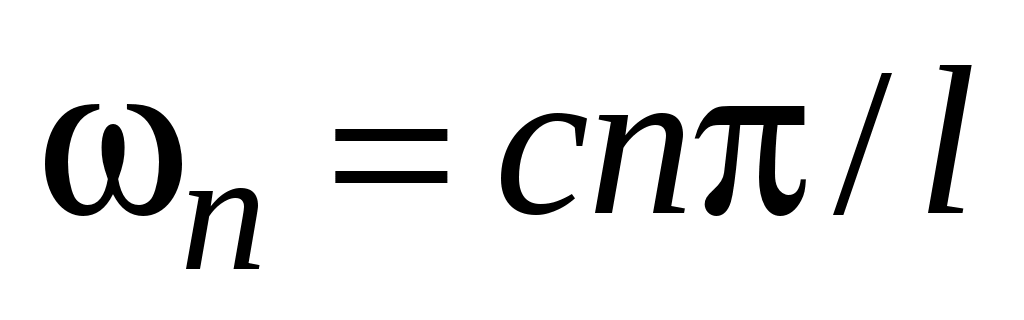 .
.
Функция f(x,t) как функция от x может быть разложена в ряд Фурье по синусам на промежутке с коэффициентами
с коэффициентами 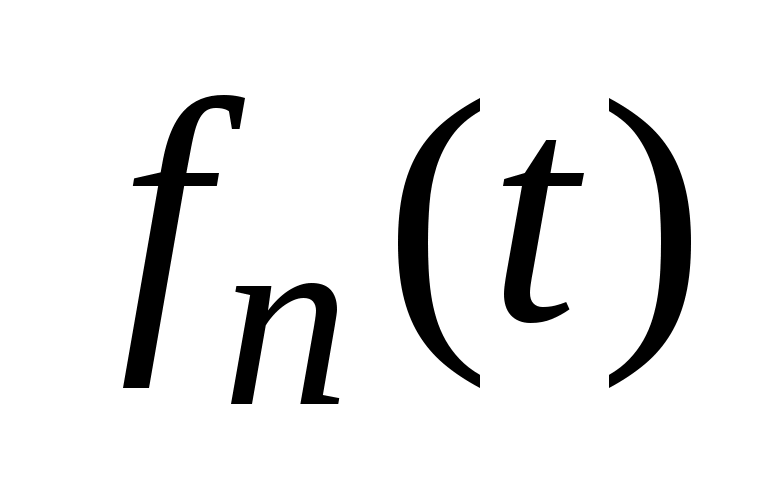 , зависящими от t:
, зависящими от t:
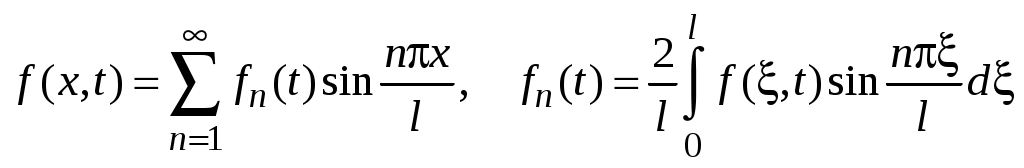 .
.
Для функции возникли два разложения в ряды Фурье по синусам; поскольку такое разложение единственно, их коэффициенты можно приравнять:
возникли два разложения в ряды Фурье по синусам; поскольку такое разложение единственно, их коэффициенты можно приравнять:
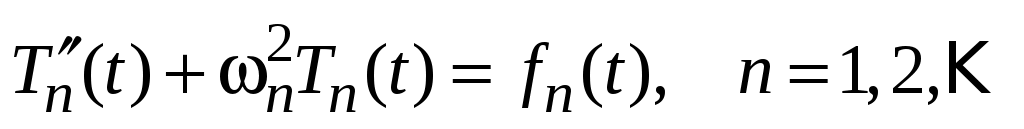 .
.
Если функции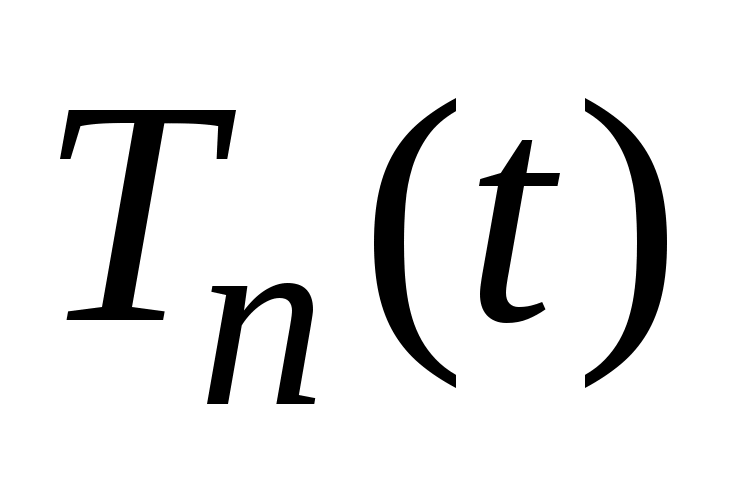 удовлетворяют этим уравнениям, функция
удовлетворяют этим уравнениям, функция  , заданная рядом (45), удовлетворяет уравнению и ГУ. Чтобы выполнялись НУ, достаточно потребовать
, заданная рядом (45), удовлетворяет уравнению и ГУ. Чтобы выполнялись НУ, достаточно потребовать  ,
, 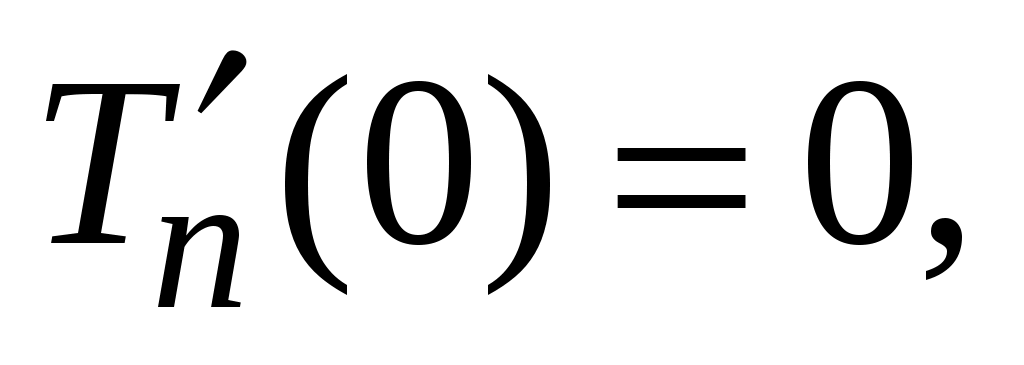
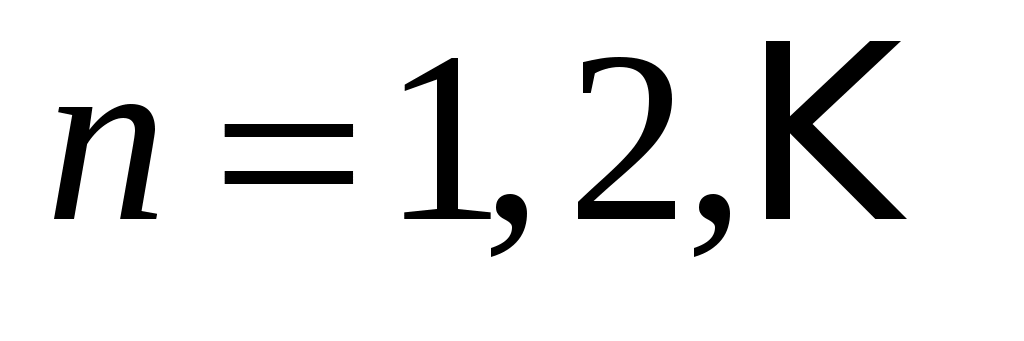 . Таким образом, функции
. Таким образом, функции 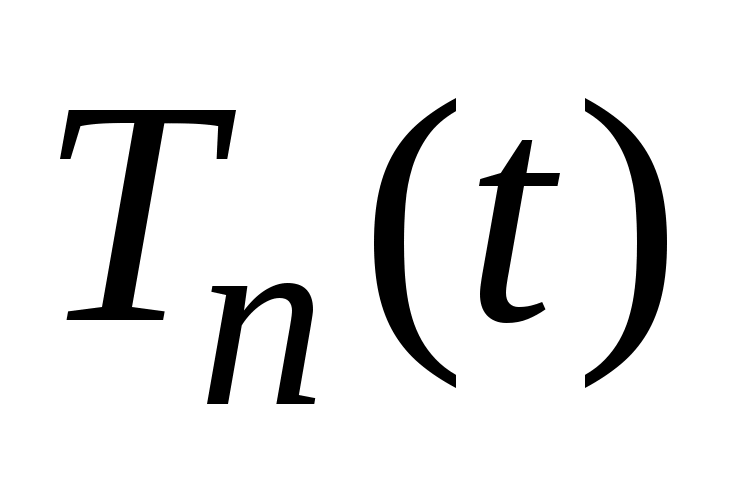 определяются задачами Коши для обыкновенных линейных неоднородных ДУ:
определяются задачами Коши для обыкновенных линейных неоднородных ДУ:
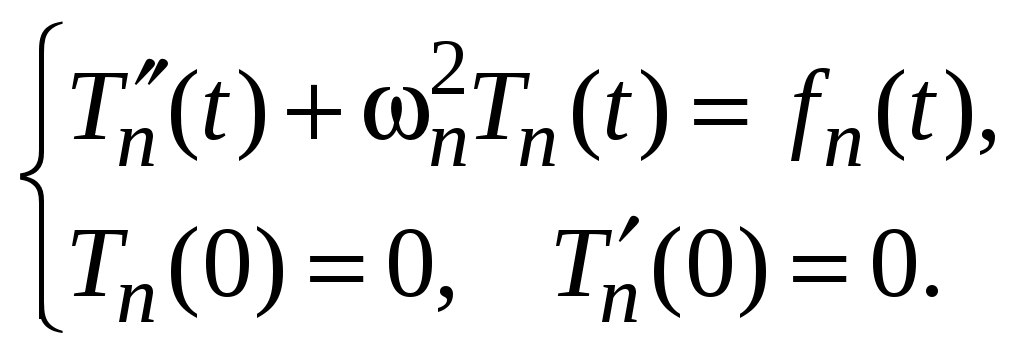 (46)
(46)
Пусть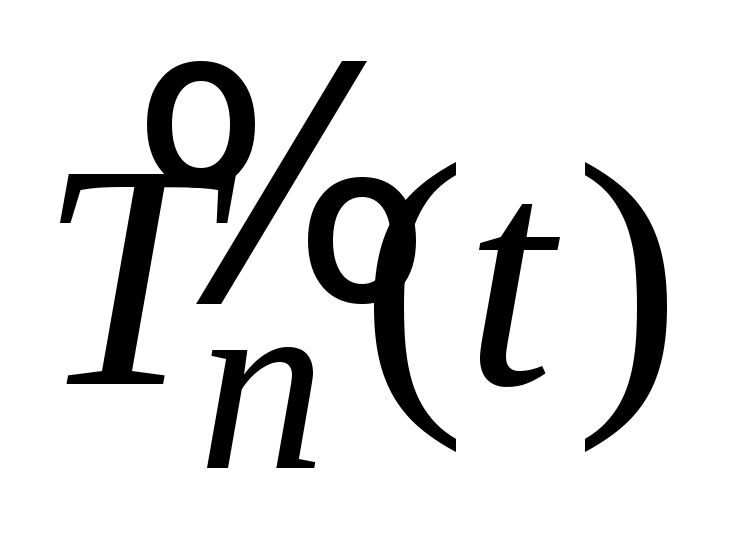 - частное решение этого неоднородного уравнения, тогда его общее решение имеет вид
- частное решение этого неоднородного уравнения, тогда его общее решение имеет вид
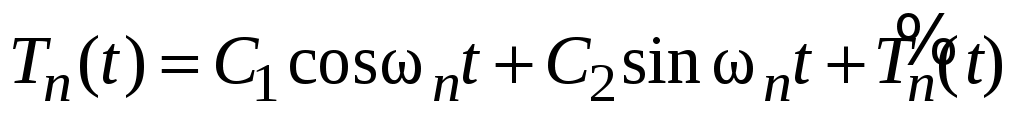 .
.
Упражнение 13. Методом вариации произвольных множителей Лагранжа
* найти частное решение уравнения из задачи (46) в виде
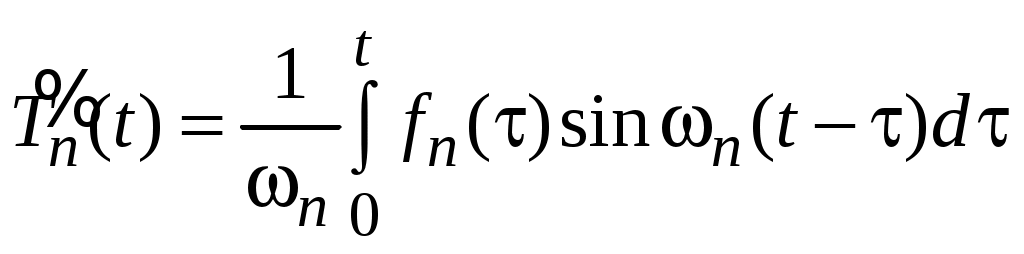 .
.
Для общего решения уравнения (46) имеем
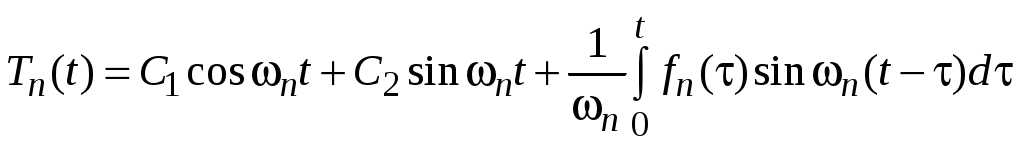 , (47)
, (47)
подстановка условий Коши дает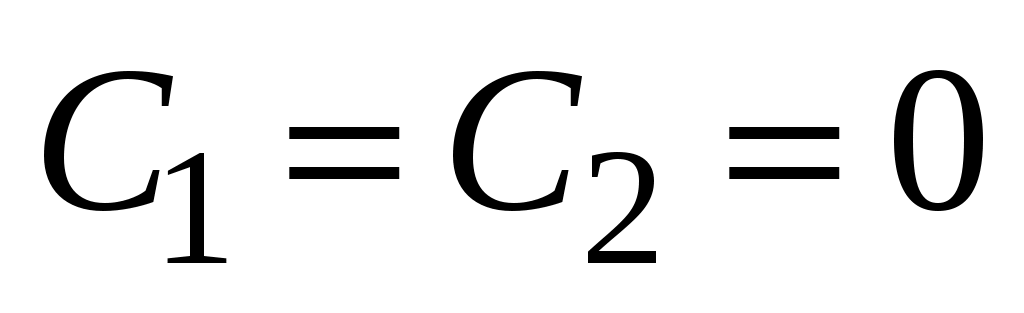 . Окончательно решение (46) принимает вид
. Окончательно решение (46) принимает вид
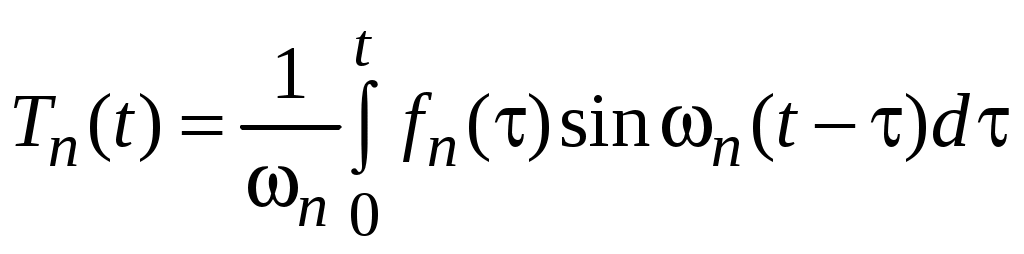 . (48)
. (48)
Подставляя в (48) выражения для коэффициентов Фурье и частот, получаем
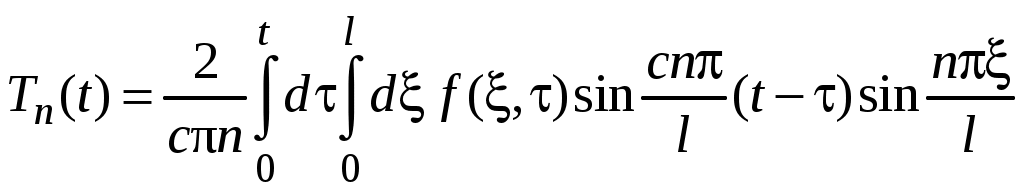 . (49)
. (49)
Ряд (45) с коэффициентами (49) дает решение задачи (44). Если функция дважды непрерывно дифференцируема и обращается в нуль на концах промежутка
дважды непрерывно дифференцируема и обращается в нуль на концах промежутка  , сумма ряда является классическим решением задачи.
, сумма ряда является классическим решением задачи.
I начально-краевая задача в общем случае состоит из неоднородного уравнения (2), неоднородных ГУ (33) и НУ (34). Ее решение следует искать в виде суммы двух функций:
 , (50)
, (50)
где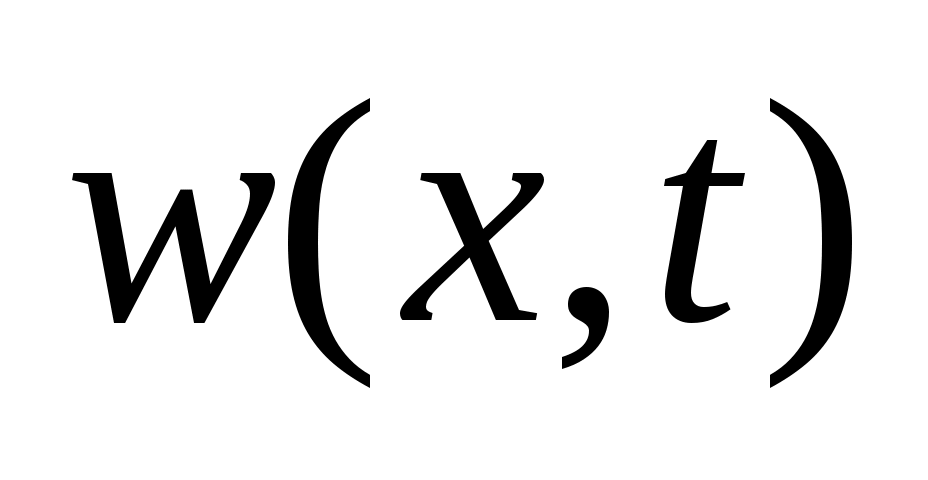 - произвольная функция, удовлетворяющая ГУ (33). Можно, например, выбрать
- произвольная функция, удовлетворяющая ГУ (33). Можно, например, выбрать 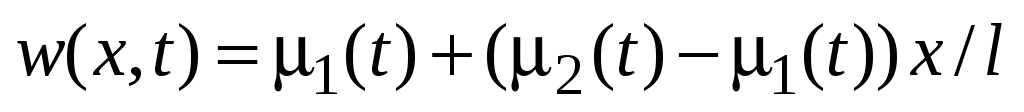 .
.
Для функции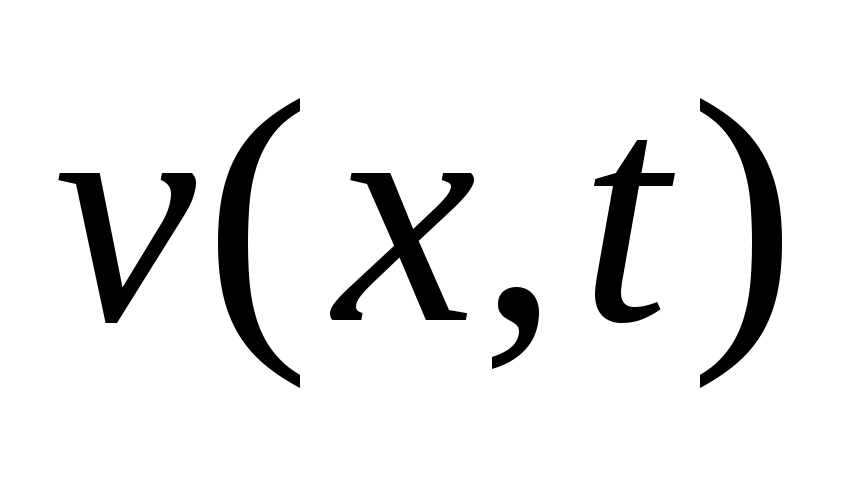 возникает НКЗ с однородными ГУ, метод решения которой изложен выше:
возникает НКЗ с однородными ГУ, метод решения которой изложен выше:
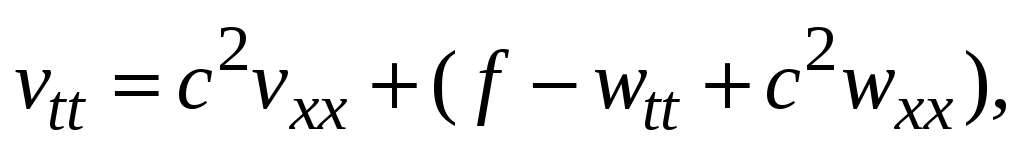
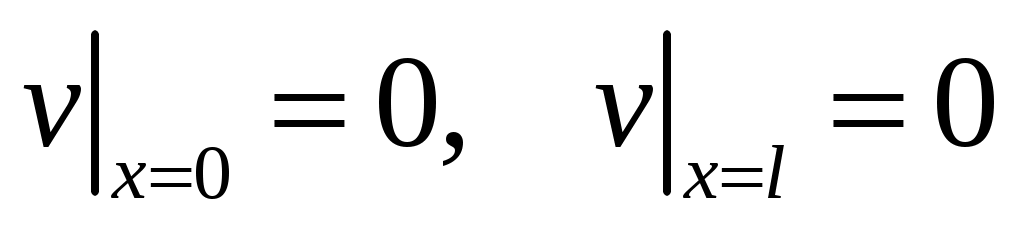
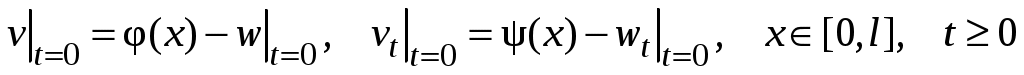 .
.
Частные случаи вынужденных колебаний струны с закрепленными концами.
1.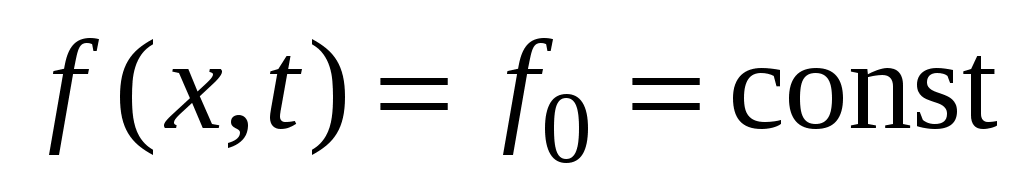 , т.е. на струну действует постоянная распределенная сила; например, горизонтальная струна находится в однородном поле силы тяжести. В этом случае решение НКЗ (2), (34), (35) проще искать в виде суммы
, т.е. на струну действует постоянная распределенная сила; например, горизонтальная струна находится в однородном поле силы тяжести. В этом случае решение НКЗ (2), (34), (35) проще искать в виде суммы
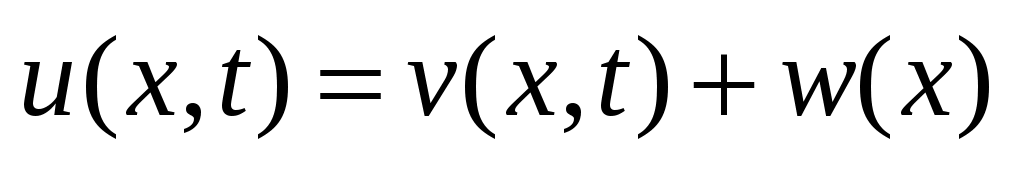 , где функция
, где функция 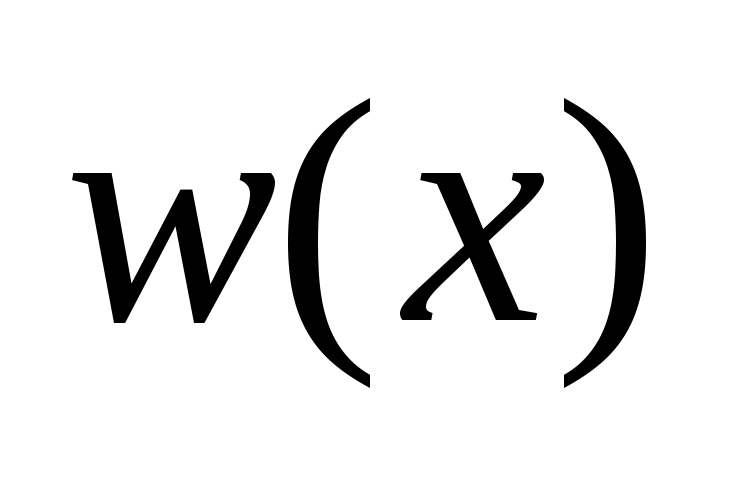 удовлетворяет уравнению (2) и ГУ (35), т.е.
удовлетворяет уравнению (2) и ГУ (35), т.е. 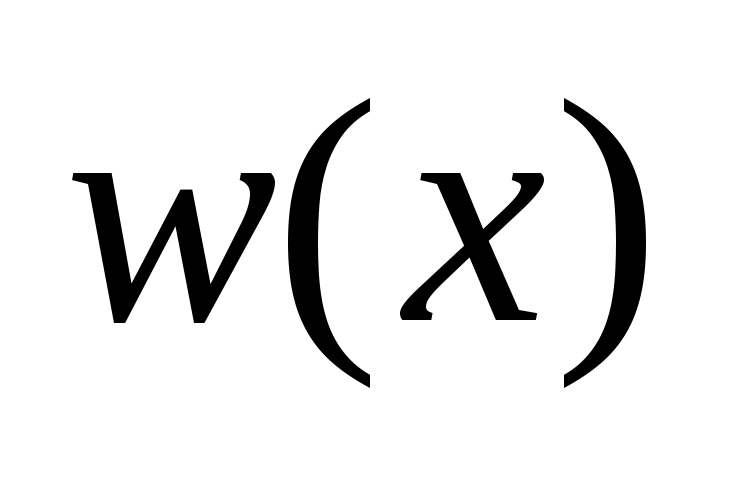 определяется краевой задачей для ОДУ:
определяется краевой задачей для ОДУ:
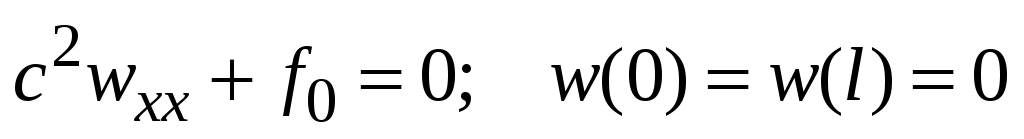 .
.
Решение этой задачи, описывающее статический прогиб струны, найдено в упражнении 1: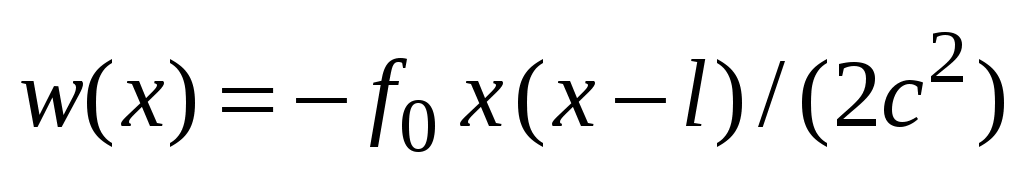 .
.
Функция должна быть решением однородного уравнения (3) с однородными ГУ (35) и неоднородными НУ:
должна быть решением однородного уравнения (3) с однородными ГУ (35) и неоднородными НУ:
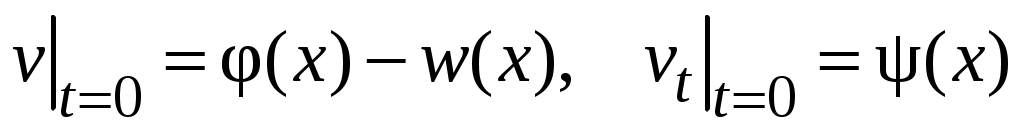 .
.
 описывает свободные колебания струны около положения равновесия, эта задача решена в § 6.
описывает свободные колебания струны около положения равновесия, эта задача решена в § 6.
2. Действующая на струну распределенная сила постоянна во времени, но может меняться от точки к точке,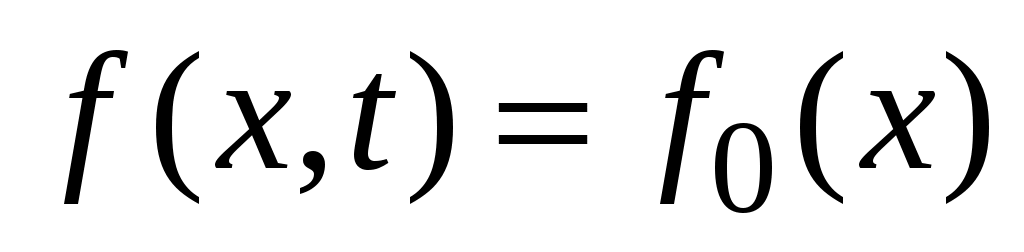 . Отличие от предыдущего случая состоит только в том, что для функции
. Отличие от предыдущего случая состоит только в том, что для функции 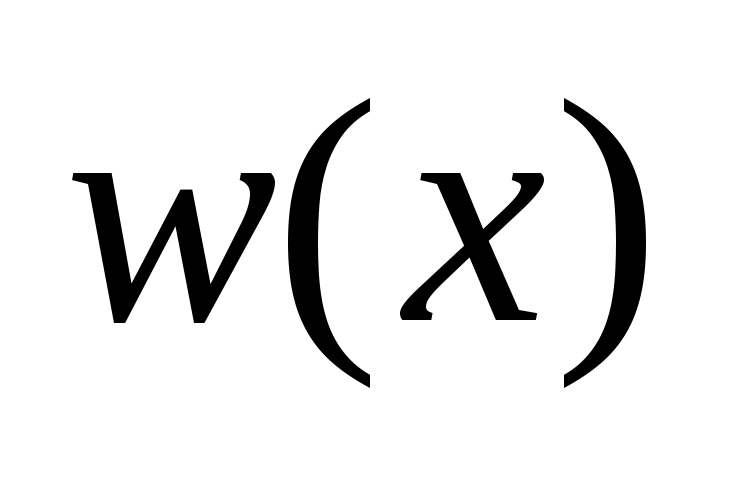 возникает более сложная КЗ:
возникает более сложная КЗ:
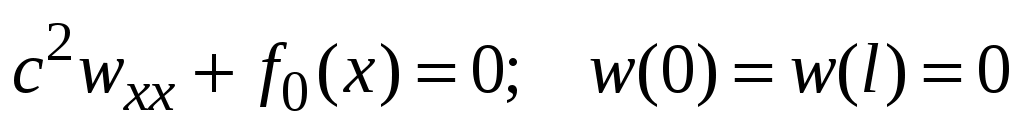 .
.
Упражнение 14. Получить решение задачи для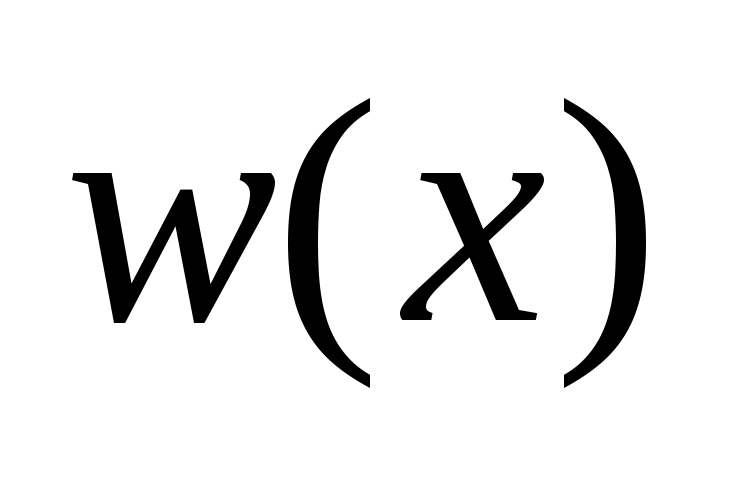 в виде
в виде
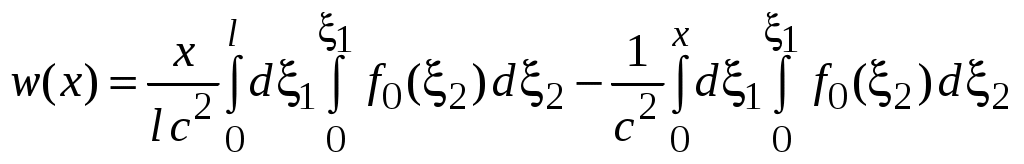 .
.
3. Приложенная к струне распределенная сила меняется по гармоническому закону: . Решение НКЗ (2), (34), (35) будем искать в виде суммы (50), в которой функция
. Решение НКЗ (2), (34), (35) будем искать в виде суммы (50), в которой функция  - частное решение уравнения (2), удовлетворяющее ГУ (35). Функция
- частное решение уравнения (2), удовлетворяющее ГУ (35). Функция  будет тогда решением однородного уравнения (3) с теми же ГУ (35) и произвольными НУ; такое решение построено в § 6.
будет тогда решением однородного уравнения (3) с теми же ГУ (35) и произвольными НУ; такое решение построено в § 6.
Вид функции зависит от того, совпадает или нет частота внешнего воздействия
зависит от того, совпадает или нет частота внешнего воздействия
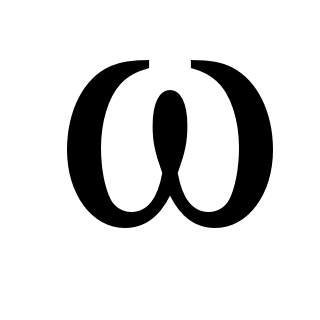 с одной из собственных частот струны
с одной из собственных частот струны 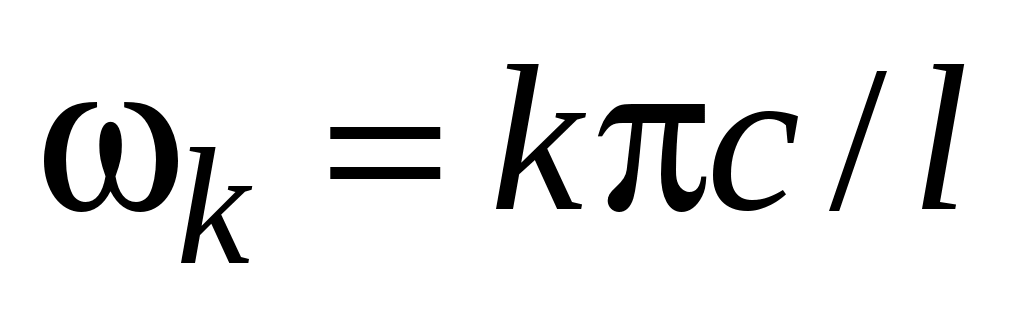 . При совпадении частот,
. При совпадении частот, 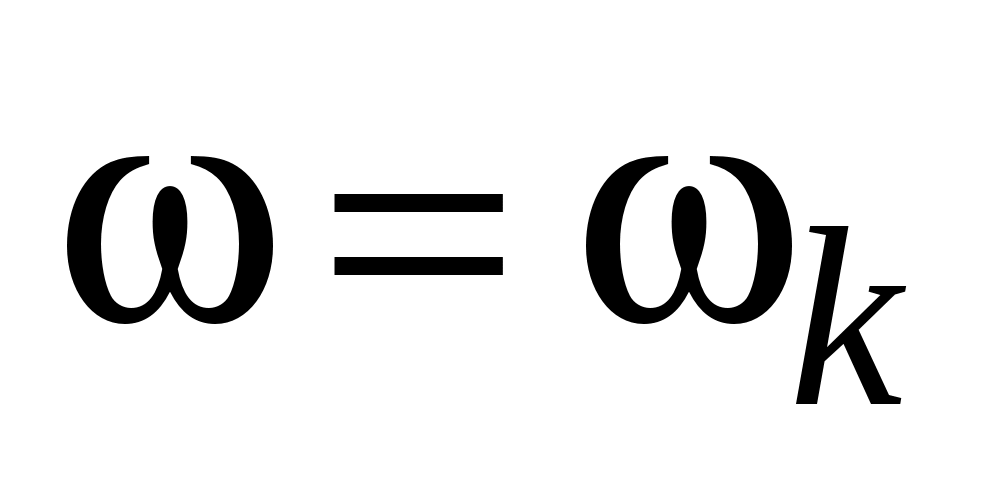 , возможно возникновение резонанса, при котором амплитуда колебаний с частотой вынуждающей силы неограниченно возрастает пропорционально времени.
, возможно возникновение резонанса, при котором амплитуда колебаний с частотой вынуждающей силы неограниченно возрастает пропорционально времени.
Упражнение 15. Построить частное решение уравнения (2) с ГУ (35), рассмотреть три случая:
1)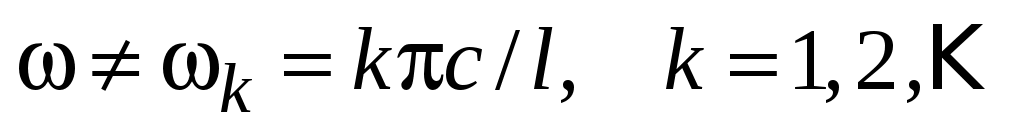 . Частное решение следует искать в виде
. Частное решение следует искать в виде
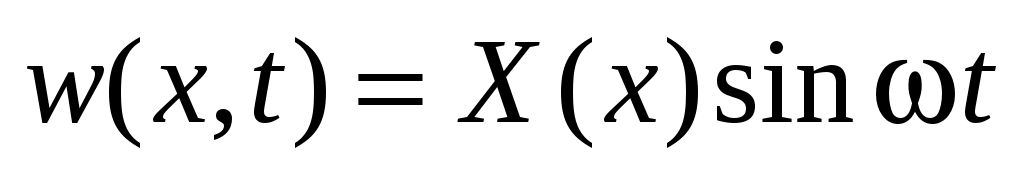 , (51)
, (51)
его подстановка в (2) и (35) дает краевую задачу для ОДУ:
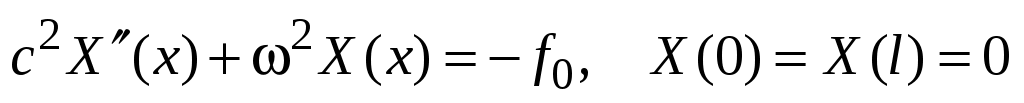 . (52)
. (52)
Выше мы уже строили общее решение такого уравнения, с точностью до обозначений оно имеет вид (47). Учет ГУ даст для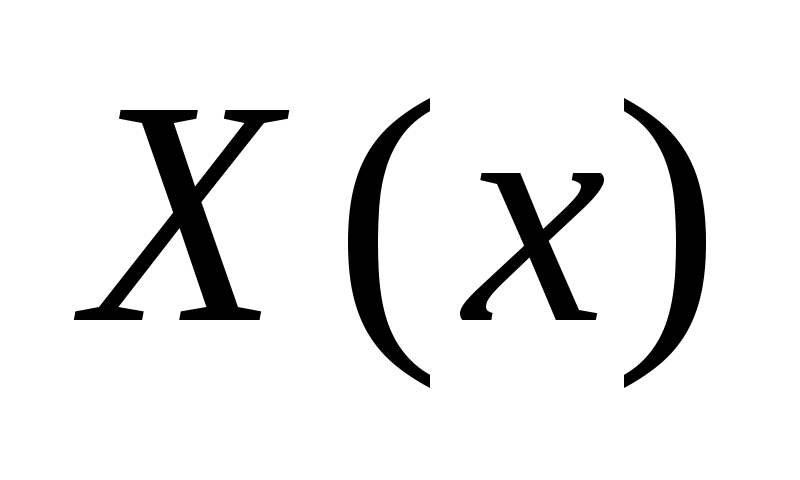 следующее выражение:
следующее выражение:
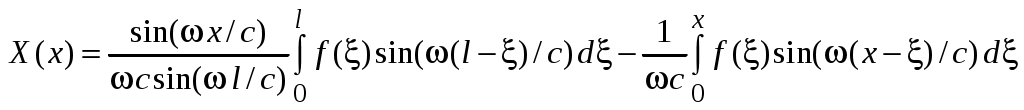 ;
;
2)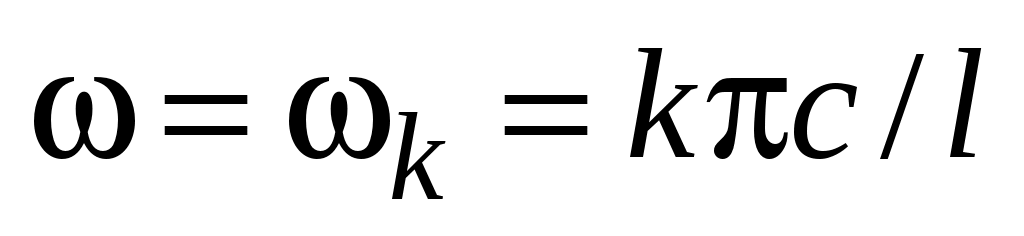 при некотором k и выполняется условие
при некотором k и выполняется условие
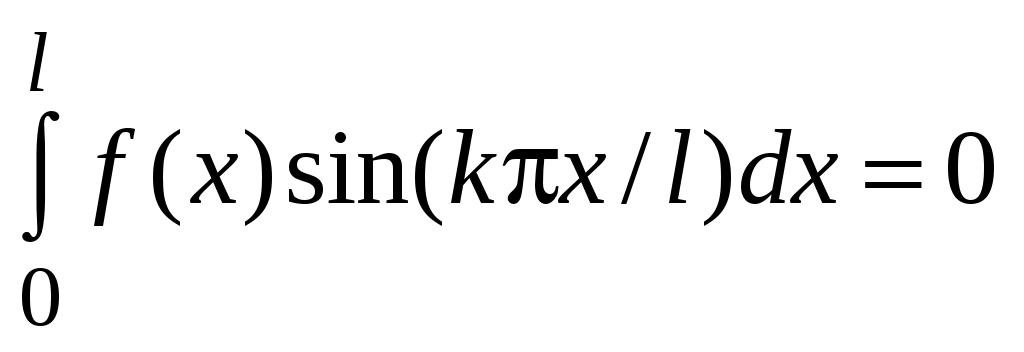 . (53)
. (53)
Частное решение по-прежнему можно искать в виде (51), где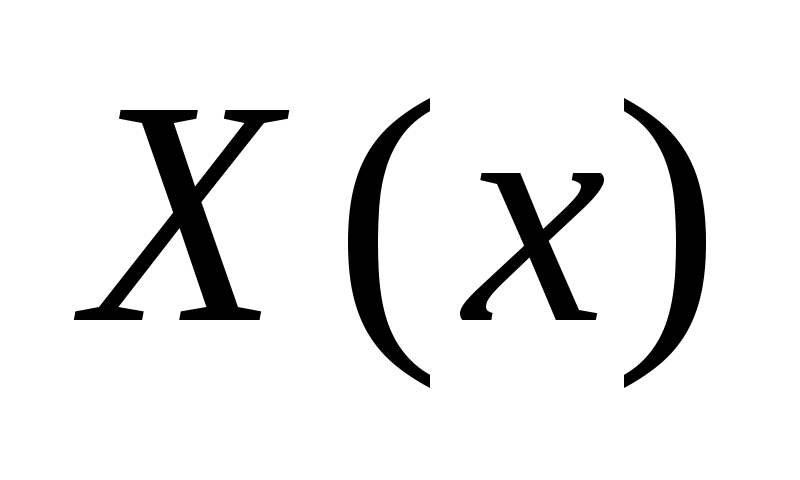 − решение задачи (52). Для
− решение задачи (52). Для 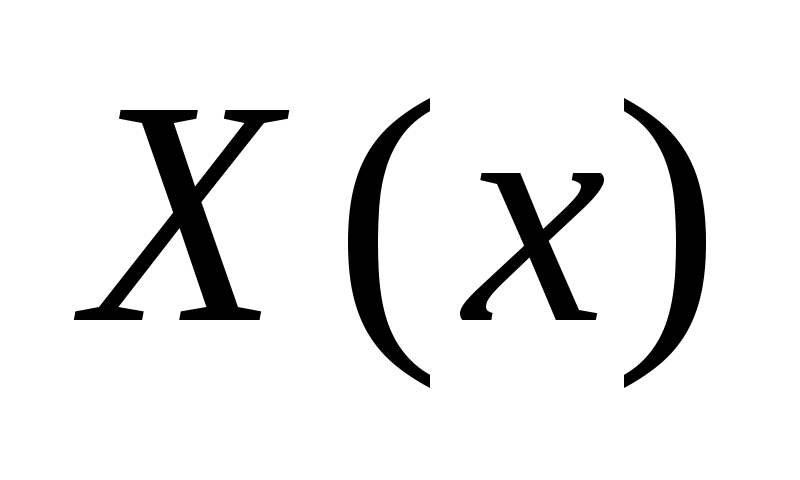 можно получить в этом случае более простое выражение:
можно получить в этом случае более простое выражение:
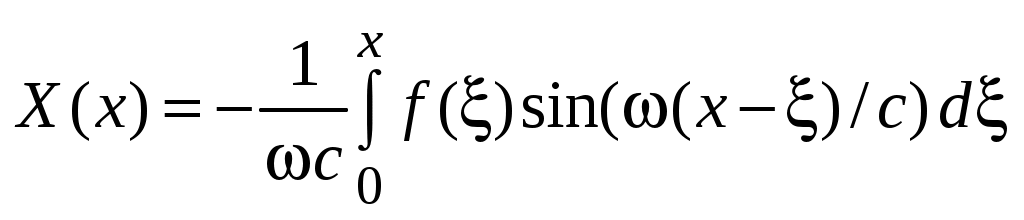 ;
;
3)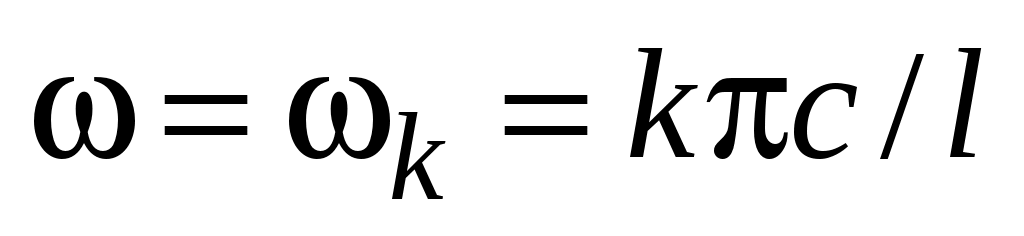 при некотором k и условие (53) не выполняется. Для частного решения можно получить
при некотором k и условие (53) не выполняется. Для частного решения можно получить
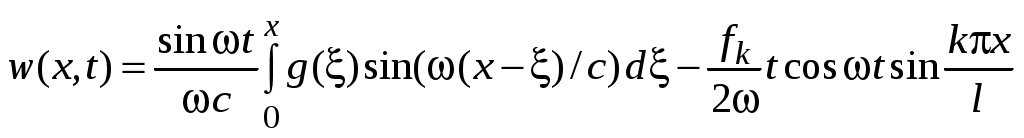 ,
,
где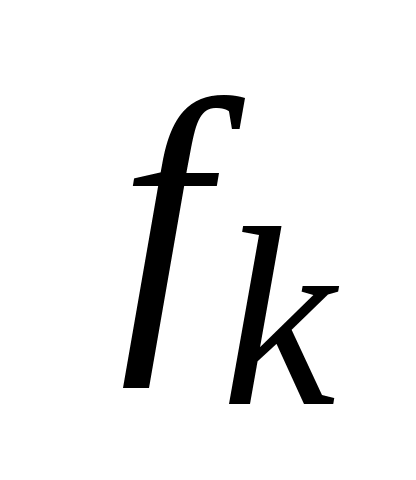 − коэффициент разложения функции
− коэффициент разложения функции 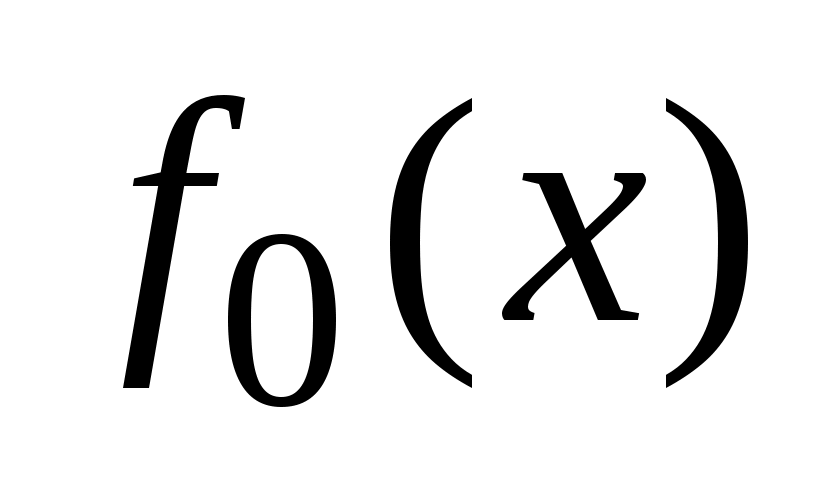 в ряд Фурье по синусам на промежутке
в ряд Фурье по синусам на промежутке  , функция
, функция 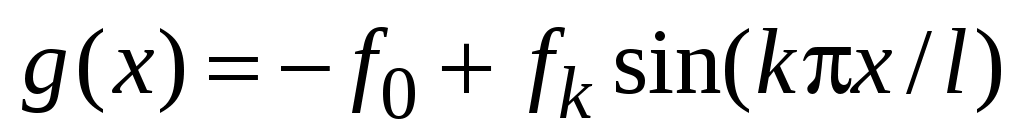 обладает тем свойством, что для нее интеграл (53) равен нулю. Видно, что второе слагаемое описывает колебание с частотой
обладает тем свойством, что для нее интеграл (53) равен нулю. Видно, что второе слагаемое описывает колебание с частотой 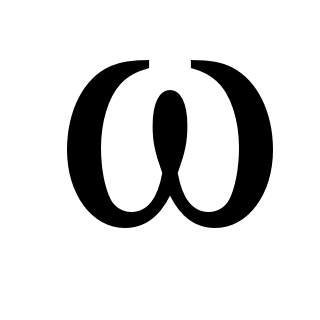 , амплитуда которого неограниченно возрастает пропорционально
, амплитуда которого неограниченно возрастает пропорционально
t.
Подстановка ряда (45) в уравнение (2) дает
следовательно,
Функция f(x,t) как функция от x может быть разложена в ряд Фурье по синусам на промежутке
Для функции
Если функции
Пусть
Упражнение 13. Методом вариации произвольных множителей Лагранжа
* найти частное решение уравнения из задачи (46) в виде
Для общего решения уравнения (46) имеем
подстановка условий Коши дает
Подставляя в (48) выражения для коэффициентов Фурье и частот, получаем
Ряд (45) с коэффициентами (49) дает решение задачи (44). Если функция
I начально-краевая задача в общем случае состоит из неоднородного уравнения (2), неоднородных ГУ (33) и НУ (34). Ее решение следует искать в виде суммы двух функций:
где
Для функции
Частные случаи вынужденных колебаний струны с закрепленными концами.
1.
Решение этой задачи, описывающее статический прогиб струны, найдено в упражнении 1:
Функция
2. Действующая на струну распределенная сила постоянна во времени, но может меняться от точки к точке,
Упражнение 14. Получить решение задачи для
3. Приложенная к струне распределенная сила меняется по гармоническому закону:
Вид функции
Упражнение 15. Построить частное решение уравнения (2) с ГУ (35), рассмотреть три случая:
1)
его подстановка в (2) и (35) дает краевую задачу для ОДУ:
Выше мы уже строили общее решение такого уравнения, с точностью до обозначений оно имеет вид (47). Учет ГУ даст для
2)
Частное решение по-прежнему можно искать в виде (51), где
3)
где
t.