ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 230
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
§3. Корректность задач математической физики. Пример некорректной задачи
Поскольку задачи матфизики описывают реальные процессы в природе, они должны удовлетворять некоторым требованиям.
Определение. Математическая задача поставлена корректно, если
− решение задачи существует;
− задача имеет единственное решение;
− решение задачи устойчиво, т.е. оно непрерывно зависит от исходных данных.
Требование устойчивости означает, что всякий физически определенный процесс должен непрерывно зависеть от начальных и граничных условий и от неоднородного члена в уравнении, т.е. должен характеризоваться функциями, которые мало меняются при малых изменениях исходных данных. В противном случае, например, двум системам практически одинаковых НУ (различие которых лежит в пределах точности измерений) могли бы соответствовать существенно разные процессы. Такие процессы не являются физически определенными. Устойчивость важна также для приближенного решения задач.
Математическую формулировку требования устойчивости покажем на примере задачи Коши (17), попутно докажем, что она устойчива.
Утверждение. Для любого промежутка времени
если только НУ различаются меньше чем на
.
Для доказательства используем формулу Даламбера (19):
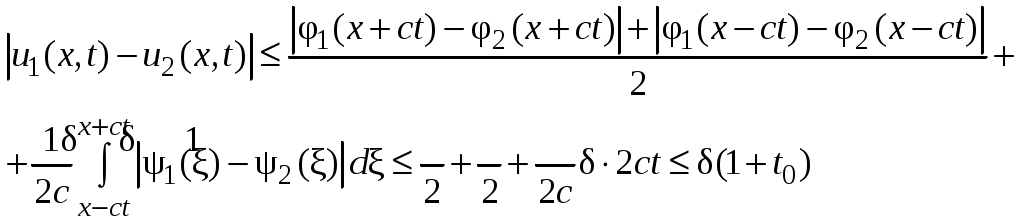
и положим
Пример Адамара* – пример некорректной задачи. Рассмотрим задачу Коши для уравнения Лапласа**:
Функции
Для любого
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
НКЗ для полубесконечной струны возникает, если один из ее концов находится далеко от исследуемого участка и не влияет на его колебания. Мы рассмотрим влияние другого, близкого, конца на распространение волны, изучим процесс отражения волн от него. Будем считать, что этот конец совпадает с точкой x= 0.
Свободные колебания струны задаются уравнением (3), в котором функция u(x,t) определяется при
Случай однородного ГУ возникает, если конец струны закреплен (свободен):
Рассмотрим сначала НКЗ (3), (25), (26). Формула Даламбера (18) дает общее решение уравнения (3), ее можно использовать и в данном случае. Но выражения
определяют эти функции только для
Подставим (18) в (26):
,
Видно, что функции
Мы получили, что задача (3), (25), (26) эквивалентна задаче Коши для бесконечной струны:
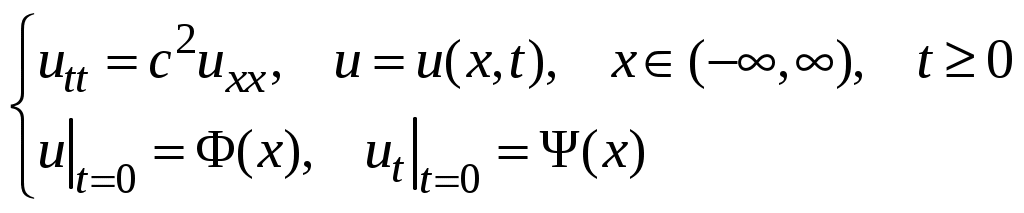
где
Решение этой последней задачи дается формулой Даламбера (19).
Выпишем решение задачи (3), (25), (26) в терминах исходных функций:
ГУ I рода:
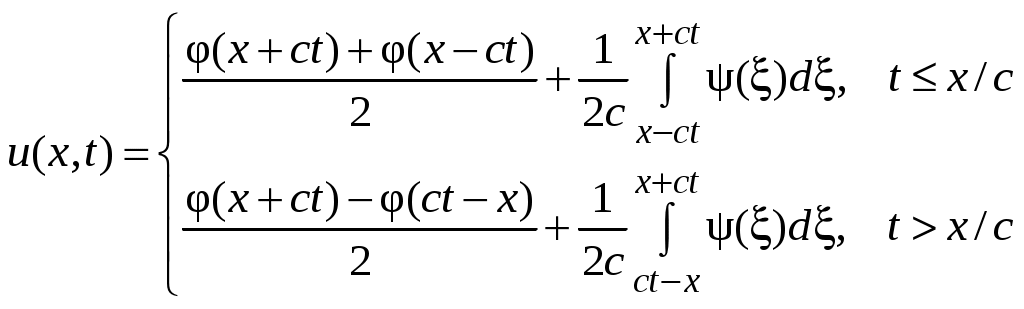 (27)
(27)ГУ II рода:
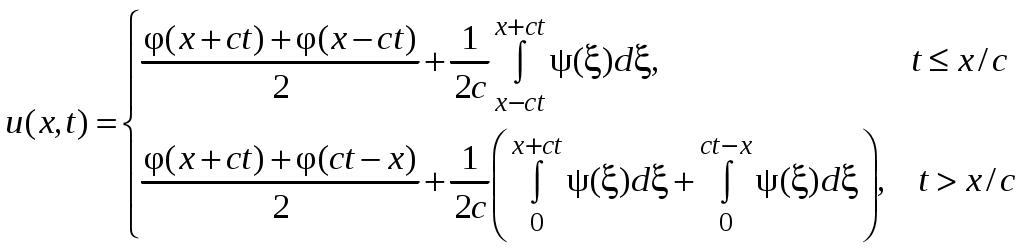 (28)
(28)Легко проверить прямой подстановкой, что если
Физическая интерпретация решения.
Пусть начальное возмущение отлично от нуля только на конечном промежутке
Область I соответствует точкам, до которых в данный момент доходят и прямая, и обратная волны от исходного возмущения; области IV и V соответствуют точкам, до которых в данный момент возмущение еще не дошло; до точек области II дошла только обратная волна, до III – только прямая. В точках области VI u= const, волна от исходного возмущения через них уже прошла, и теперь они покоятся. Области I – VI такие же, как в случае бесконечной струны.
Р
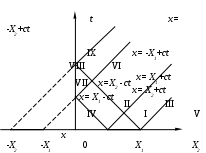 ис.8
ис.8Область VIII соответствует точкам, в которые приходит прямая волна от фиктивного возмущения:
Таким образом, действие закрепленного (свободного) конца x= 0 свелось к отражению волны смещения, связанному с сохранением абсолютной величины смещения и переменой (сохранением) его знака.
Влияние граничного режима. В случае произвольного неоднородного ГУ решение задачи (3), (24), (25) следует искать в виде суммы