ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 229
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
§1. Вывод уравнения колебаний струны, постановка задач
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера**
§3. Корректность задач математической физики. Пример некорректной задачи
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений)
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)
§6. Свободные колебания ограниченной струны. Метод Фурье* (метод разделения переменных)
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных)
этого ряда, можно было сразу искать  в виде произведения:
в виде произведения: 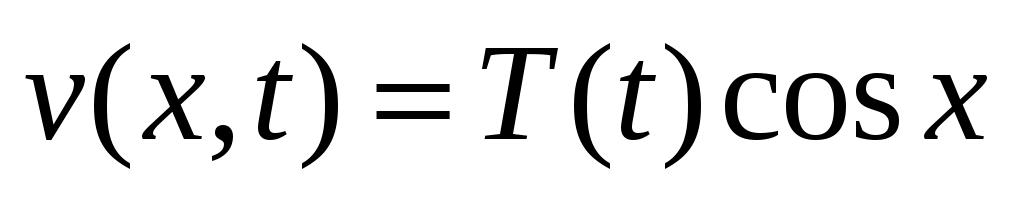 .
.
Пример 3. Решить вторую НКЗ для однородного уравнения струны:
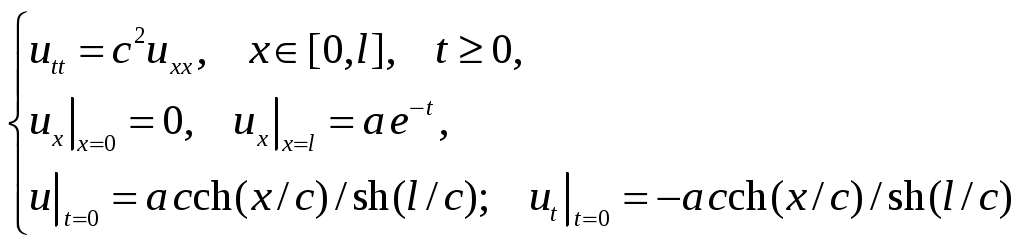
Решение задачи будем искать в виде суммы (50): , при этом попытаемся подобрать функцию
, при этом попытаемся подобрать функцию  , одновременно удовлетворяющую уравнению и ГУ; обычно это удается, если в задаче фигурируют const, exp, sin, cos. Функцию
, одновременно удовлетворяющую уравнению и ГУ; обычно это удается, если в задаче фигурируют const, exp, sin, cos. Функцию  будем искать в виде
будем искать в виде 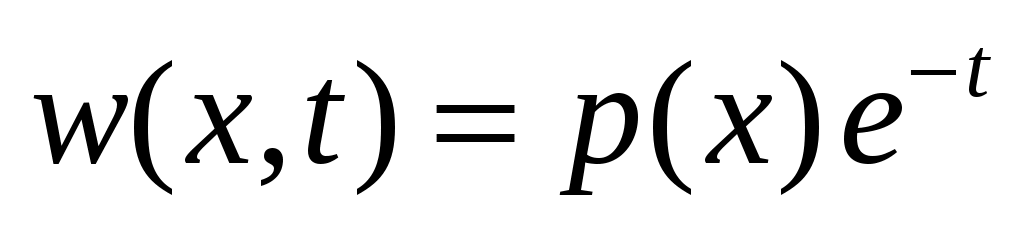 , где
, где 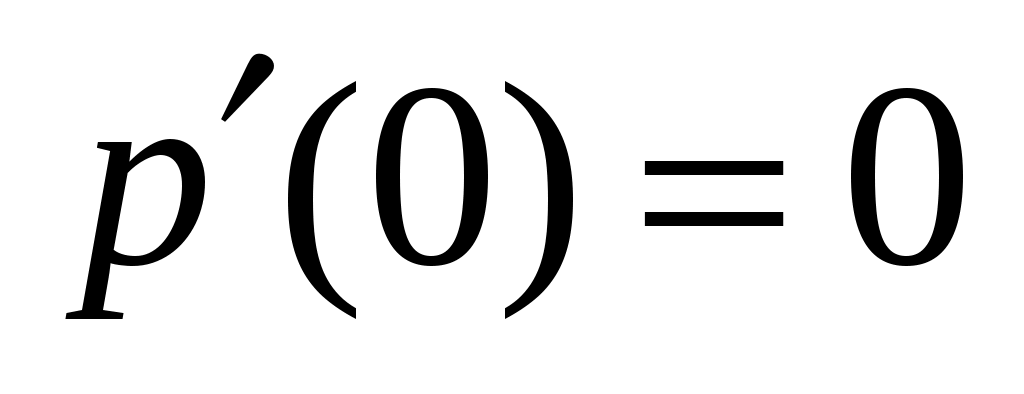 ,
, 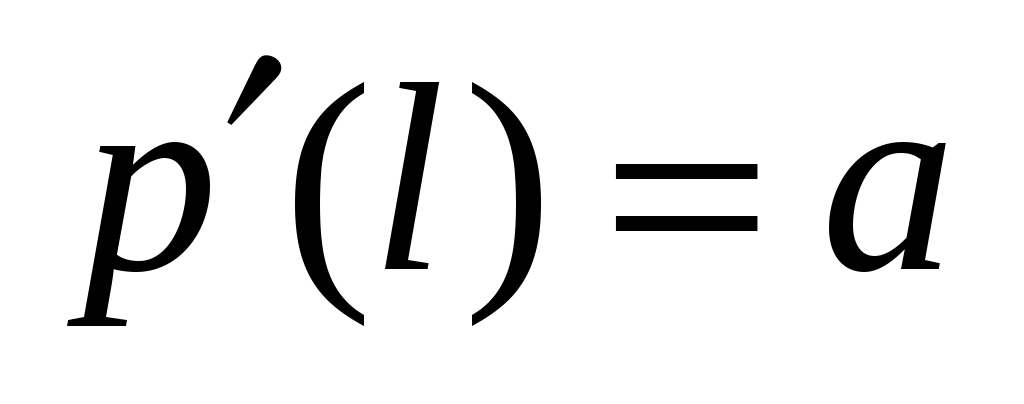 . Подстановка в уравнение дает
. Подстановка в уравнение дает 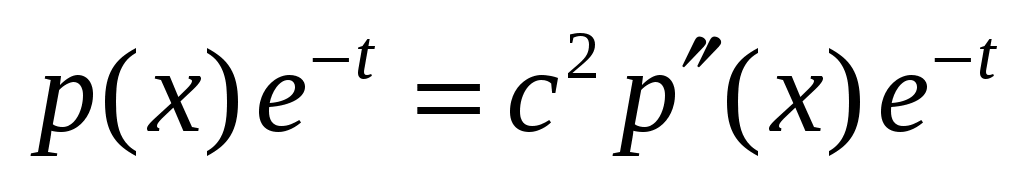 , для
, для 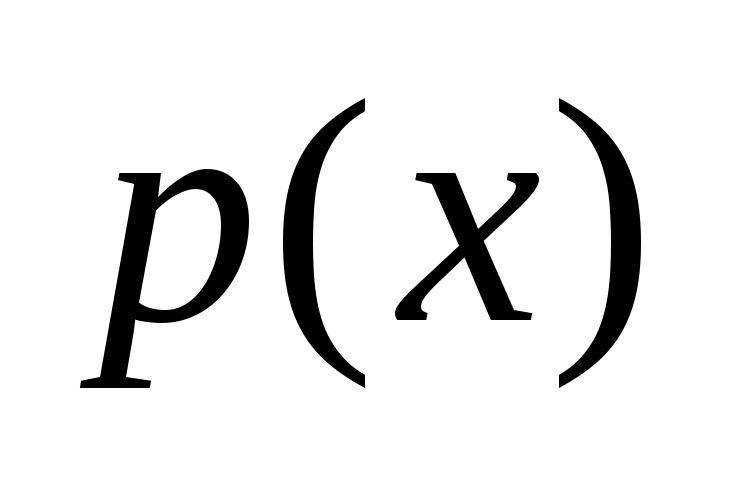 получаем уравнение
получаем уравнение  .Его общее решение имеет вид
.Его общее решение имеет вид 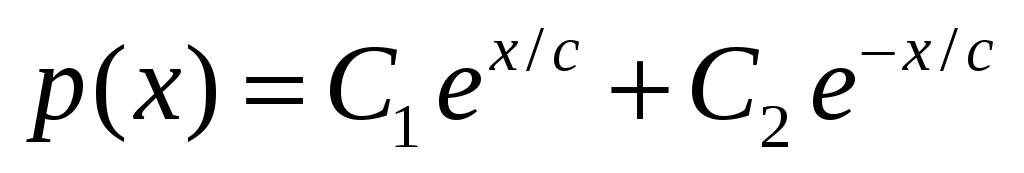 , из начальных условий следует, что
, из начальных условий следует, что 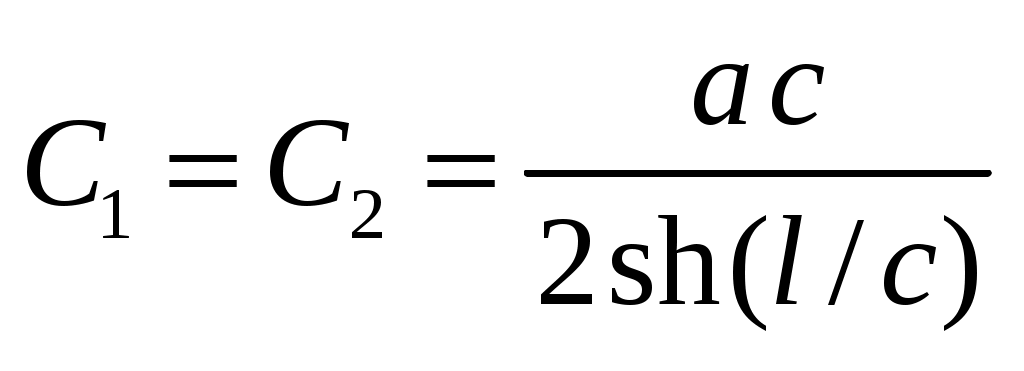 . В результате получаем
. В результате получаем
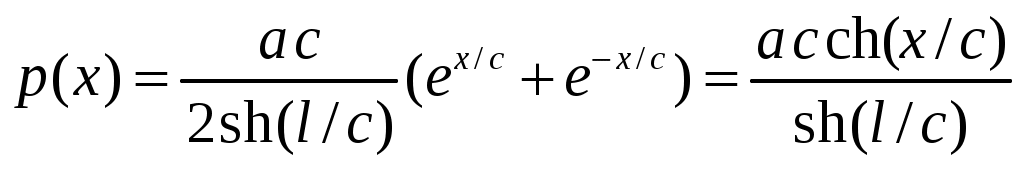 и
и 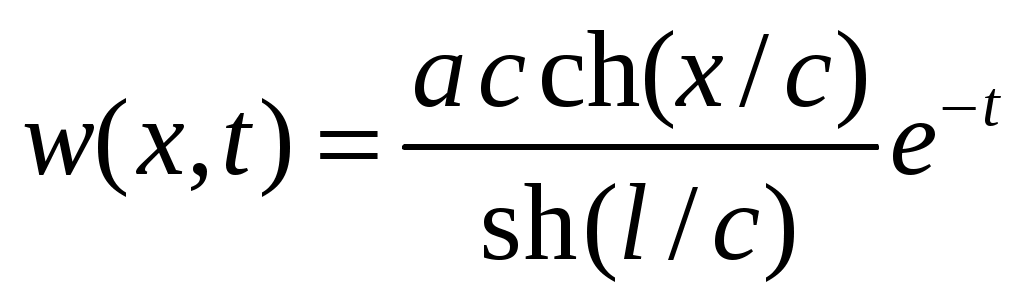 .
.
Подставим сумму в исходную задачу:
в исходную задачу:
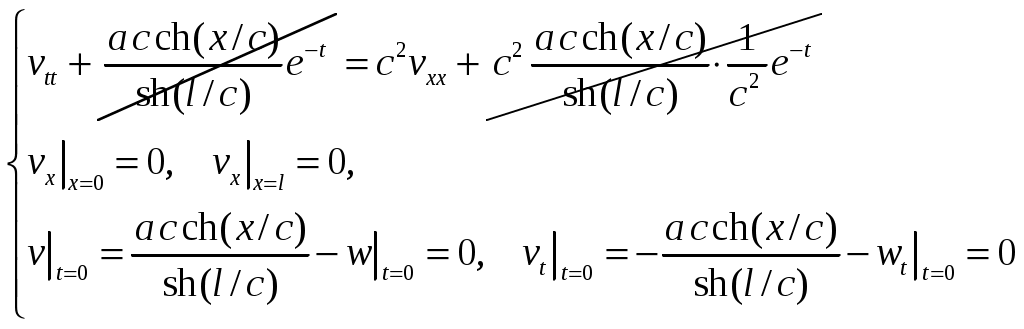
Для функции возникла задача из однородного волнового
возникла задача из однородного волнового
уравнения с однородными НУ и ГУ, которая имеет только тривиальное решение: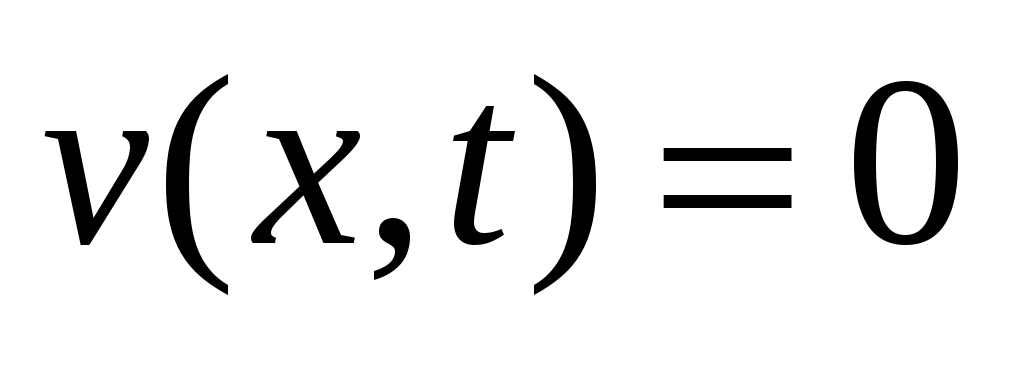 . Ответ исходной задачи:
. Ответ исходной задачи:
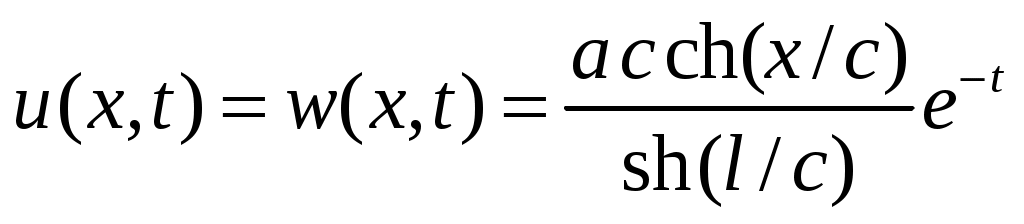
.
Отметим, что в общем случае при таком методе решения для функции возникает задача из однородного уравнения с однородными граничными и неоднородными начальными условиями. Для граничных условий II рода ее решение следует искать в виде ряда:
возникает задача из однородного уравнения с однородными граничными и неоднородными начальными условиями. Для граничных условий II рода ее решение следует искать в виде ряда:
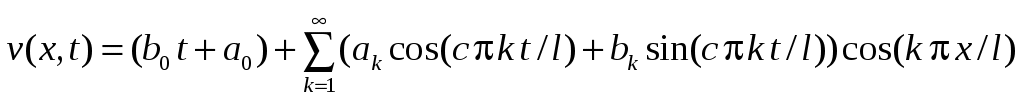 .
.
20. Однородная струна со свободным концом и закрепленным концом
и закрепленным концом  имеет в начальный момент форму квадратичной параболы:
имеет в начальный момент форму квадратичной параболы: 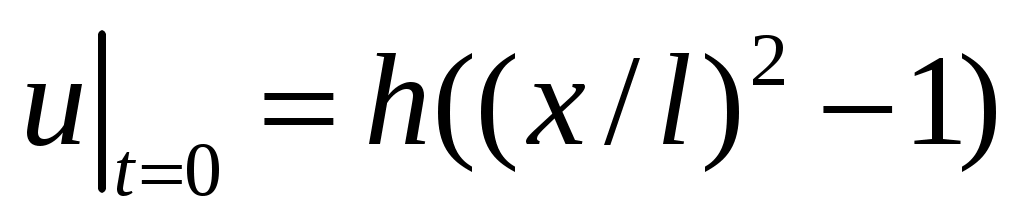 . Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
. Определить смещение точек струны от прямолинейного положения равновесия, предполагая, что начальные скорости отсутствуют.
21. Однородная струна, закрепленная на конце и свободная на конце
и свободная на конце  , находится в прямолинейном положении равновесия. В момент времени
, находится в прямолинейном положении равновесия. В момент времени  она получает в точке x0 удар от молоточка, который сообщает этой точке скоростьv0. Описать свободные колебания струны. Молоточек считать плоским, шириной
она получает в точке x0 удар от молоточка, который сообщает этой точке скоростьv0. Описать свободные колебания струны. Молоточек считать плоским, шириной 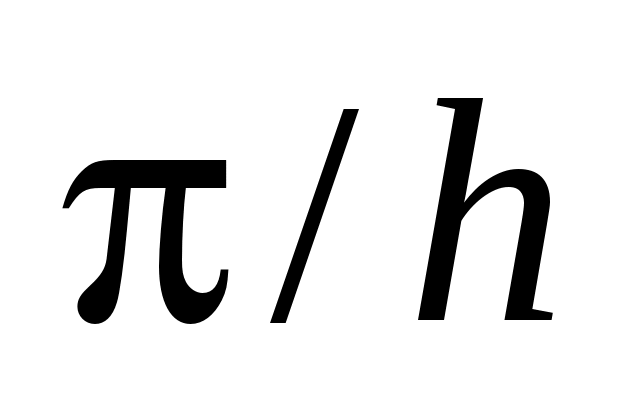 :
:
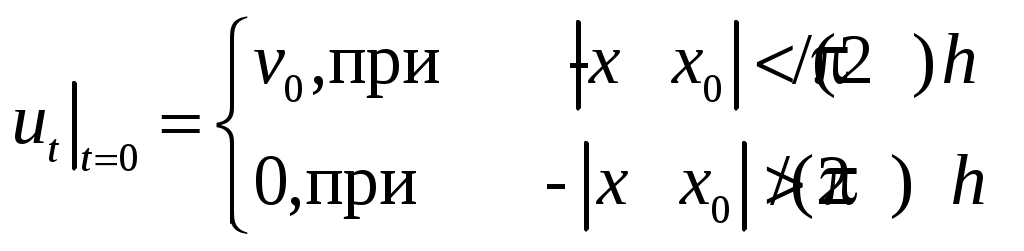
22. Однородная струна, свободная на конце и закрепленная на конце
и закрепленная на конце  , находится в прямолинейном положении равновесия. В момент времени
, находится в прямолинейном положении равновесия. В момент времени  она получает в точке x0 удар от молоточка, который сообщает этой точке скоростьv0. Описать свободные колебания струны. Молоточек считать выпуклым, шириной
она получает в точке x0 удар от молоточка, который сообщает этой точке скоростьv0. Описать свободные колебания струны. Молоточек считать выпуклым, шириной 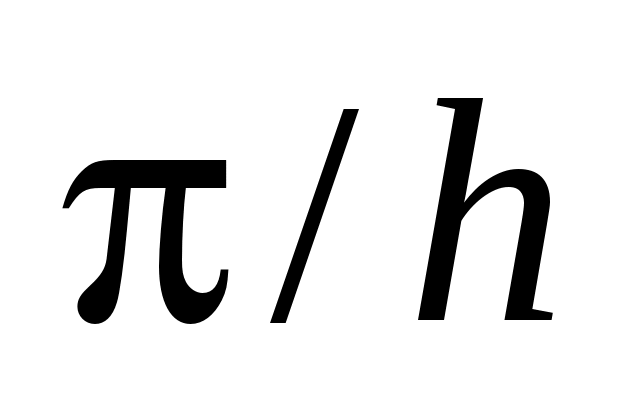 :
:
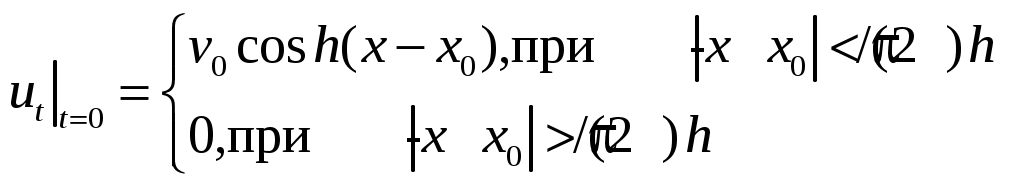
23. Описать продольные колебания цилиндрического стержня,
один конец которого свободен, а к другому с момента приложена сила
приложена сила 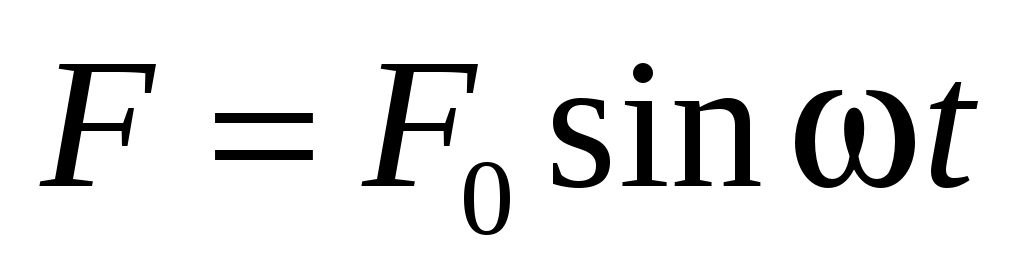 , направление которой совпадает с осью стержня. (Считать, что
, направление которой совпадает с осью стержня. (Считать, что  не совпадает с собственными частотами стержня.)
не совпадает с собственными частотами стержня.)
24. На струну длиной l действует внешняя возмущающая сила, плотность которой равна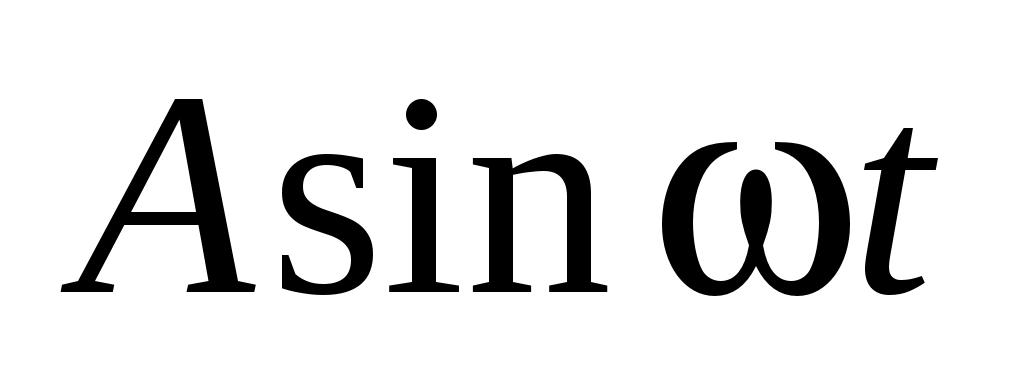 (
( не совпадает с собственными частотами струны). Найти закон колебаний струны, если начальные отклонения и скорости равны нулю, левый конец струны закреплен, а правый свободен.
не совпадает с собственными частотами струны). Найти закон колебаний струны, если начальные отклонения и скорости равны нулю, левый конец струны закреплен, а правый свободен.
В задачах 25 – 28 функция определена при
определена при  ,
,  .
.
25.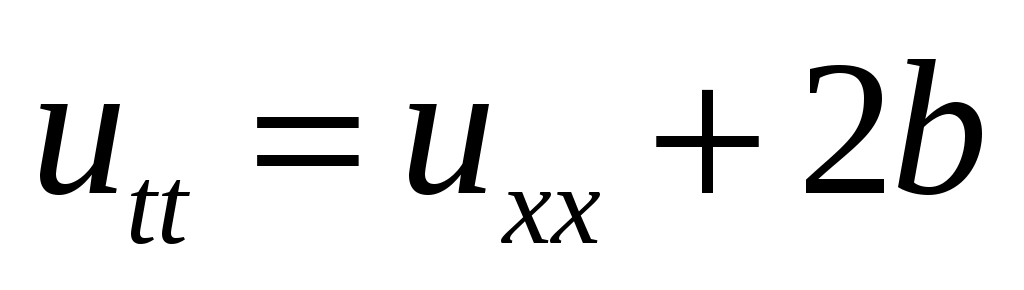 ,
, 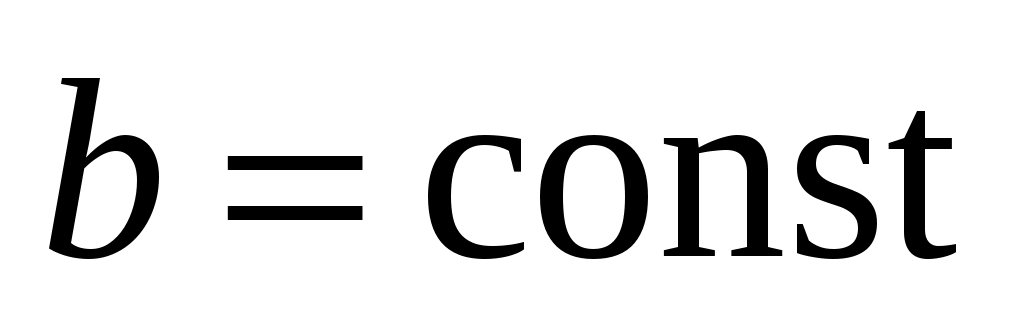 ,
, 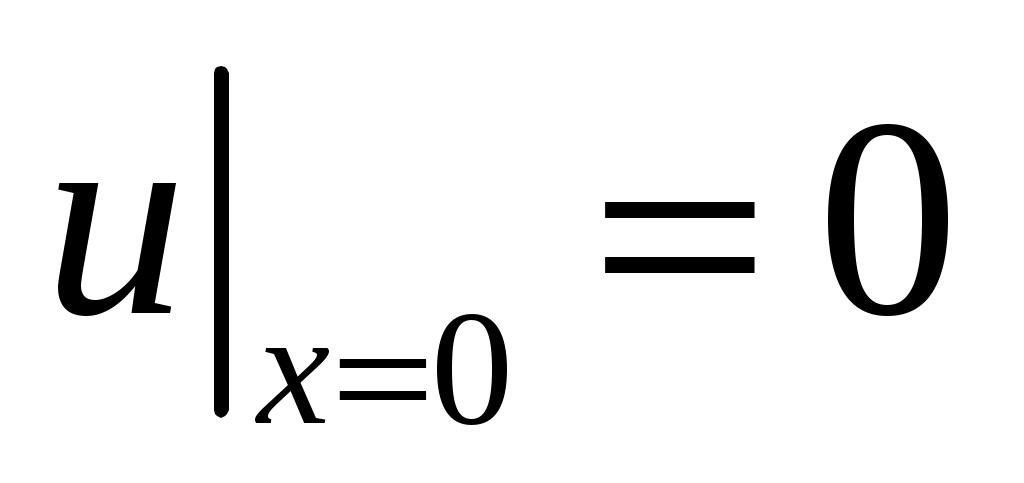 ,
, 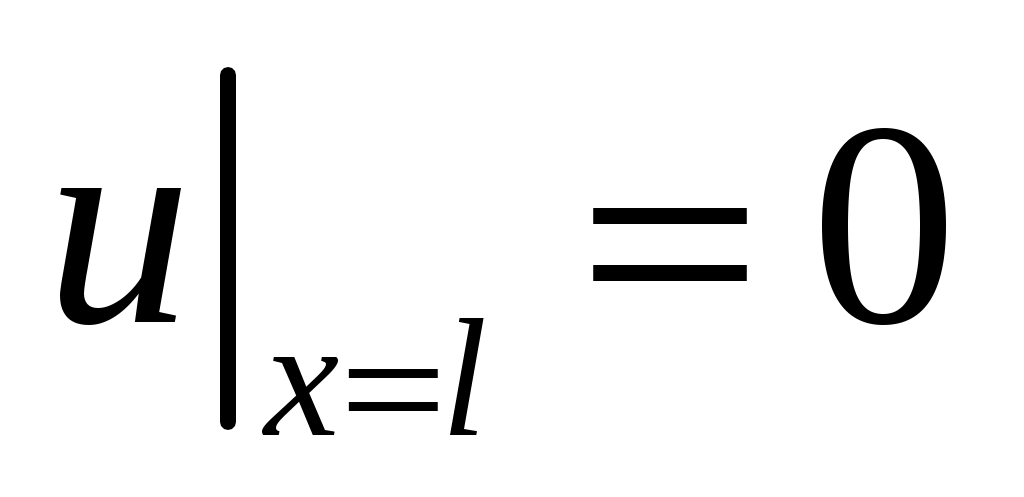 ,
, 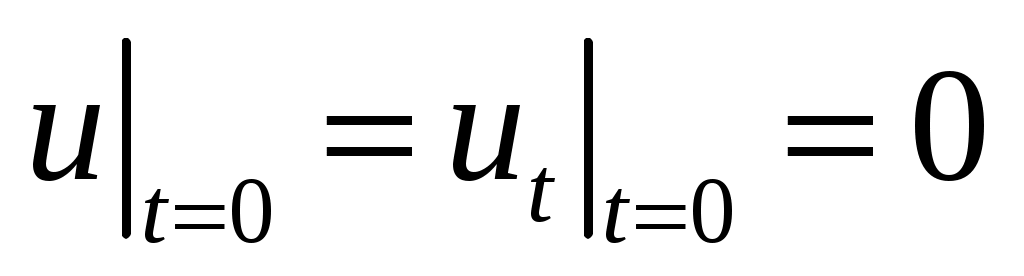 .
.
26.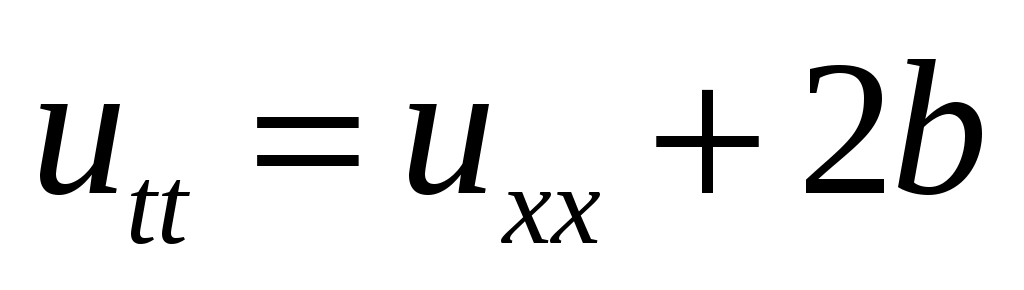 ,
, 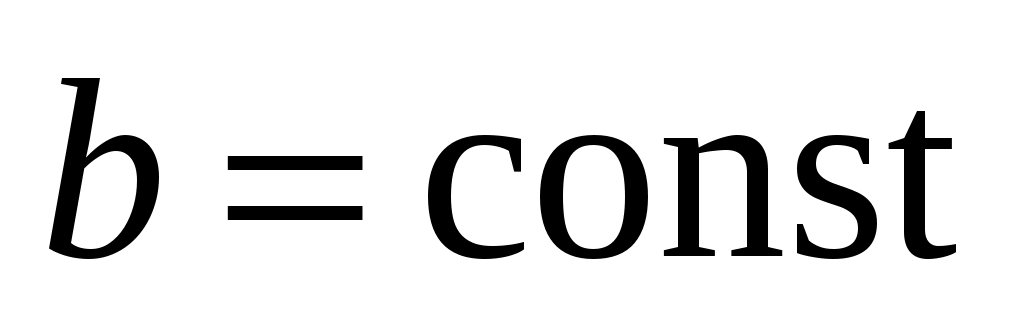 ,
, 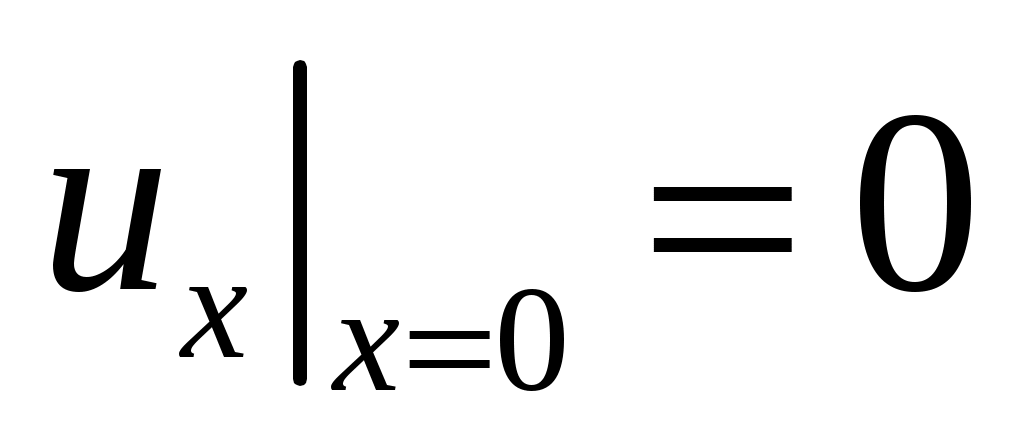 ,
, 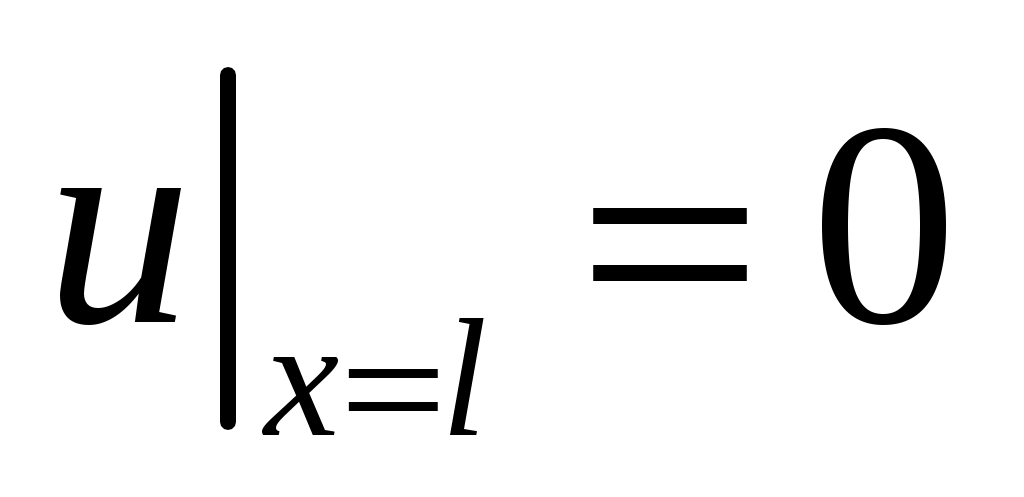 ,
, 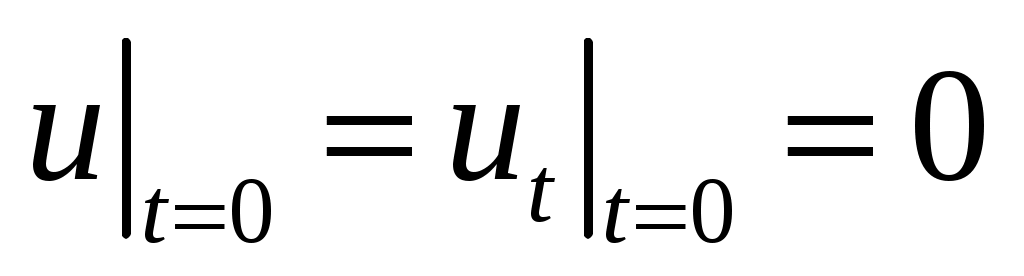 .
.
27. ,
, 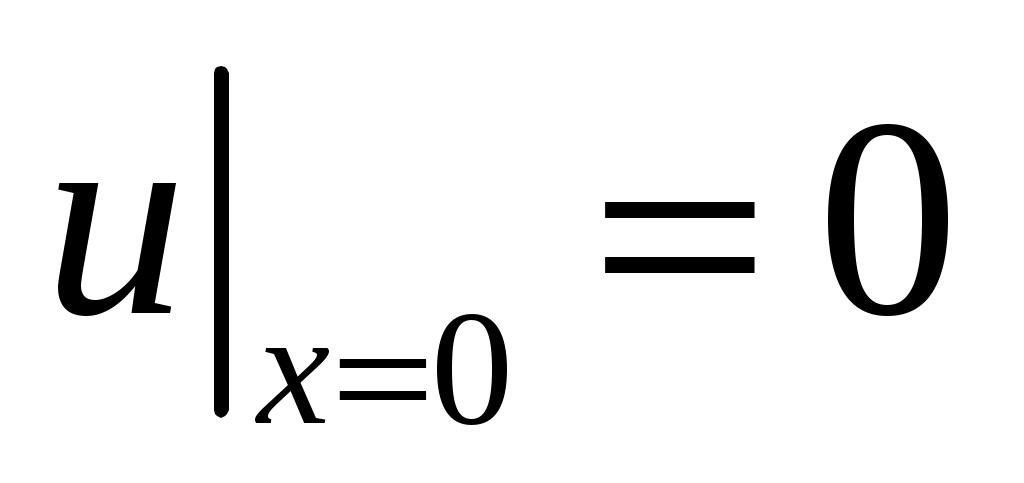 ,
,  ,
, 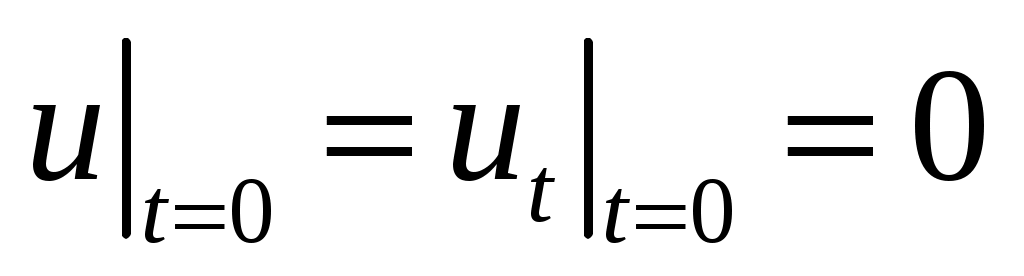
.
28. ,
, 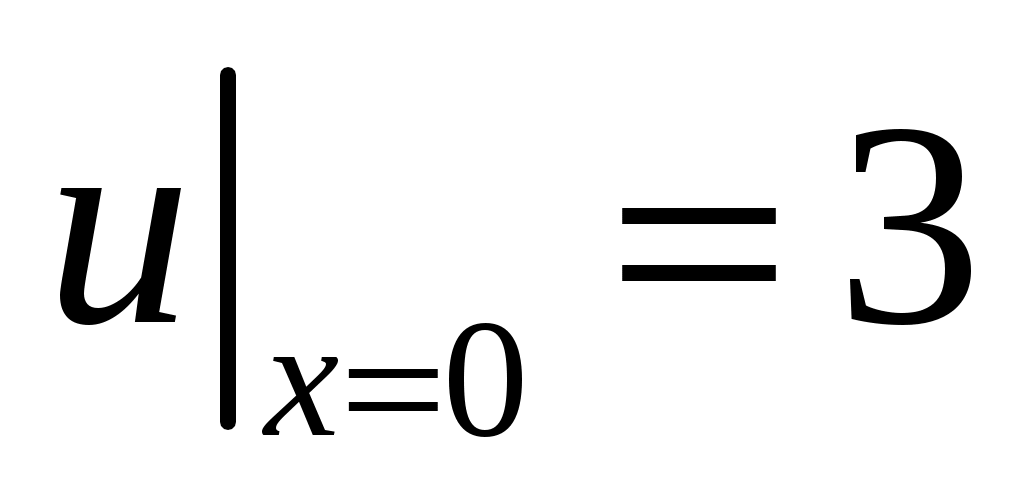 ,
, 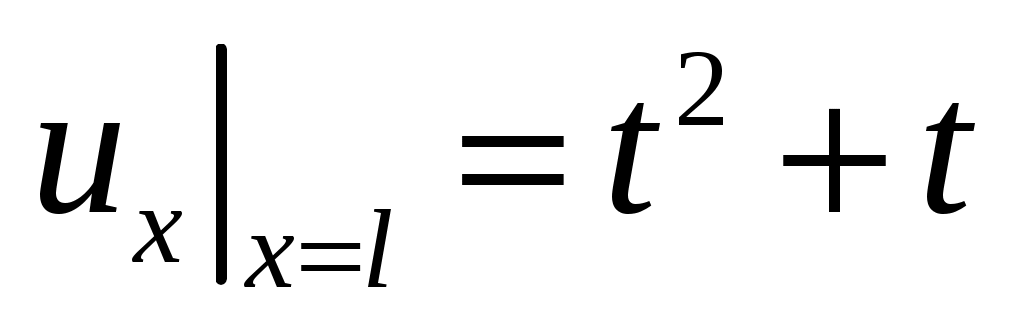 ,
,  .
.
В задачах 29–32 функция определена при
определена при 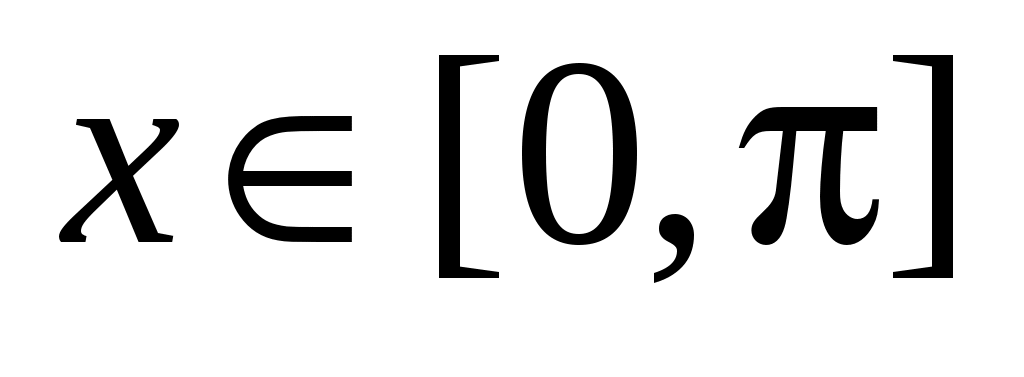 ,
,  .
.
29.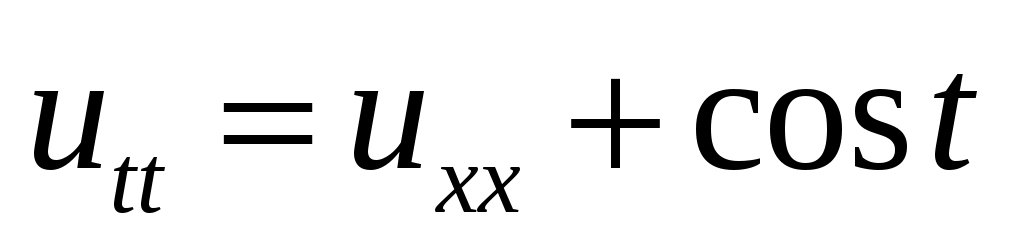 ,
, 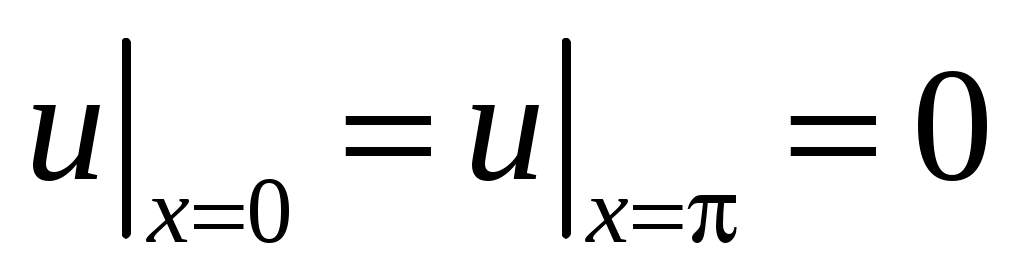 ,
,  .
.
30.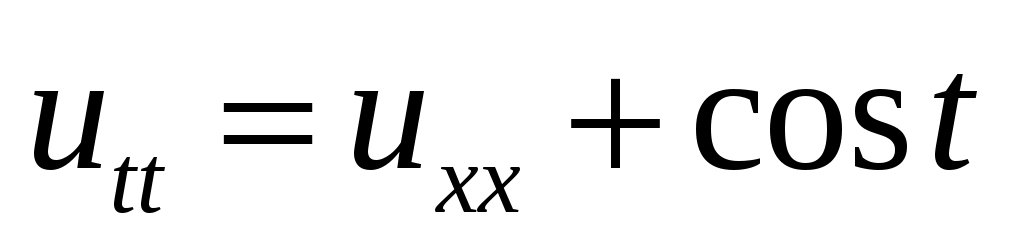 ,
, 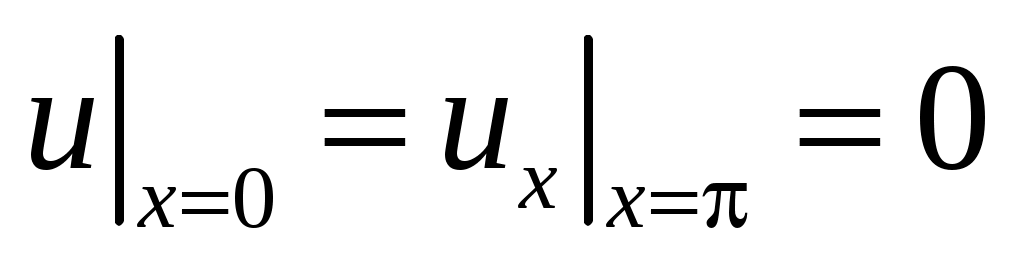 ,
,  .
.
31.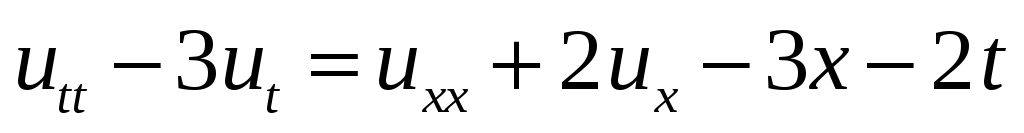 ,
,
 ,
, 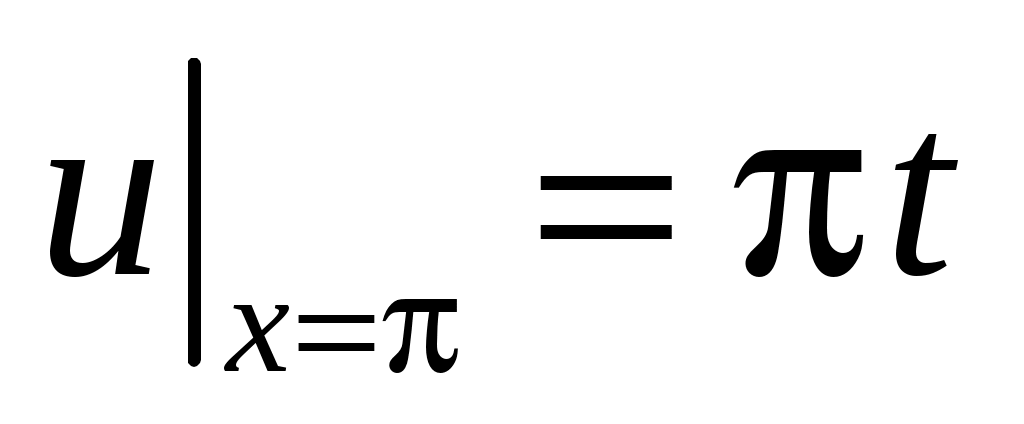 ,
, 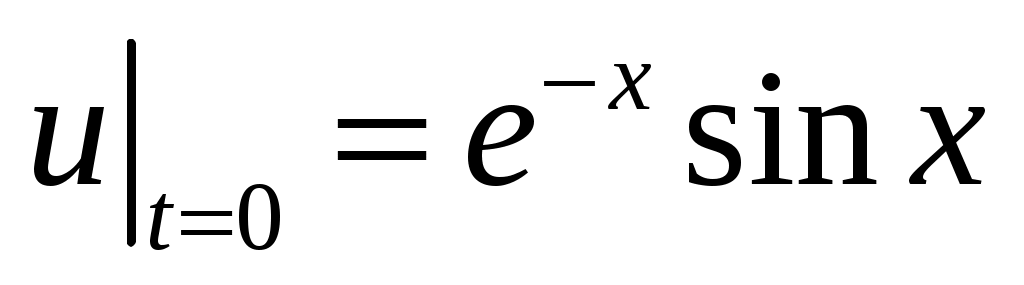 ,
, 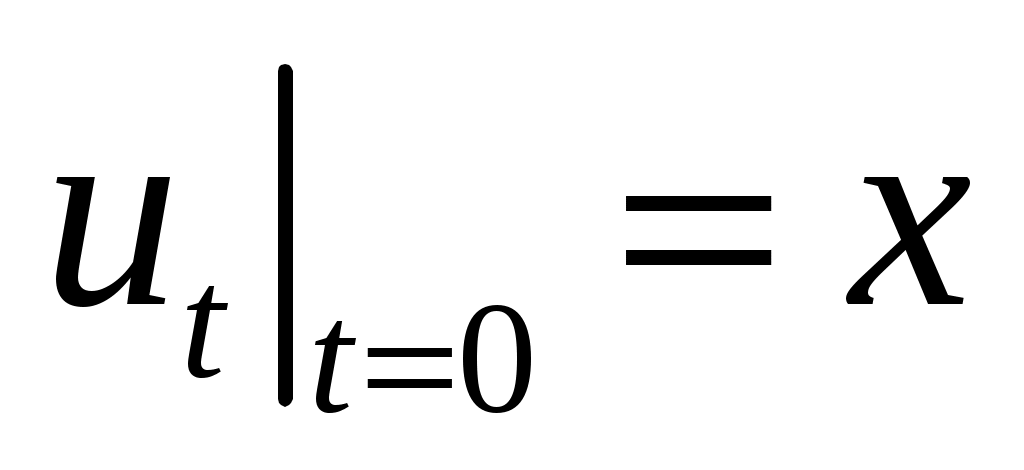 .
.
32.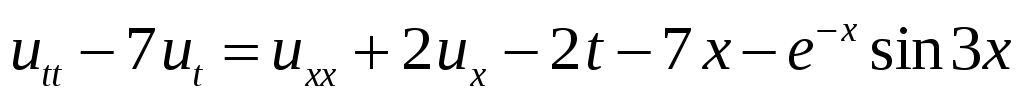 ,
,
 ,
, 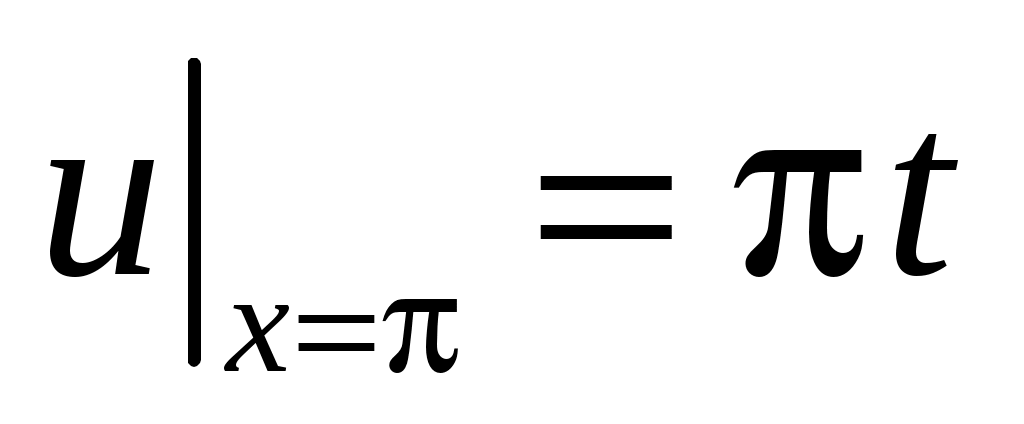 ,
, 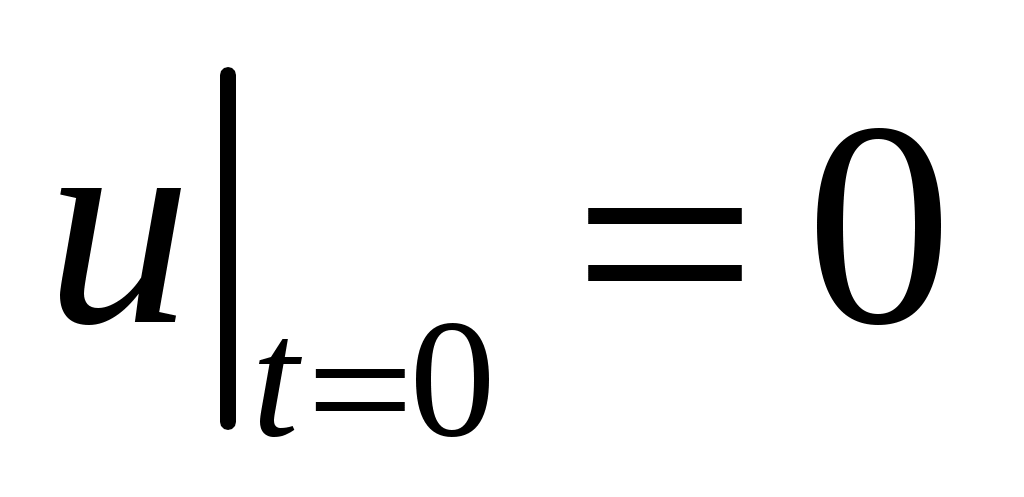 ,
, 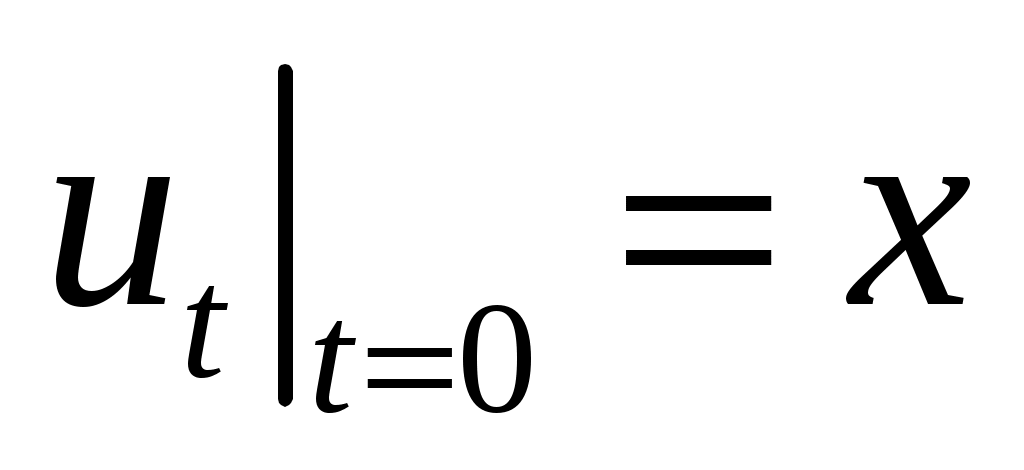 .
.
В задачах 33–35 функция определена при
определена при 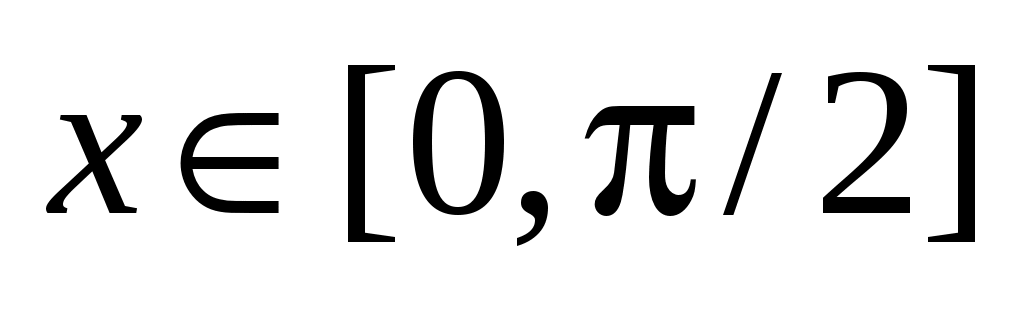 ,
,  .
.
33.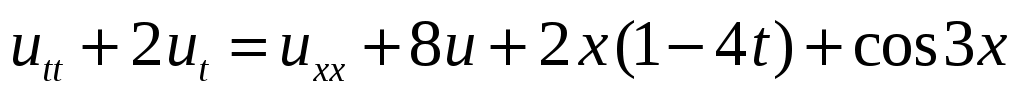
,
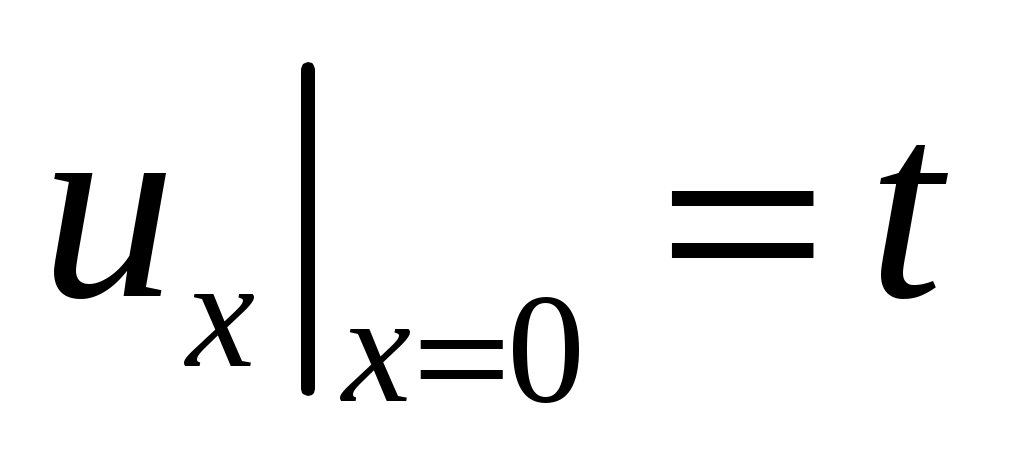 ,
, 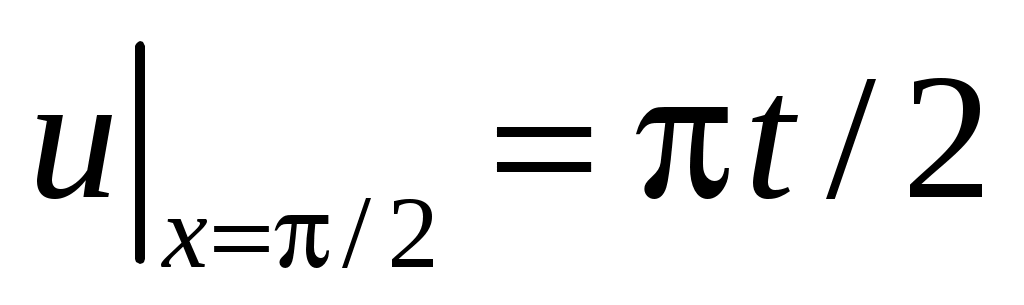 ,
,  ,
,  .
.
34.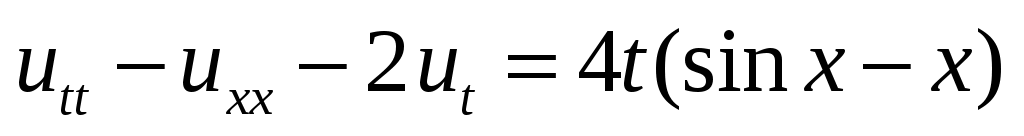 ,
,
 ,
, 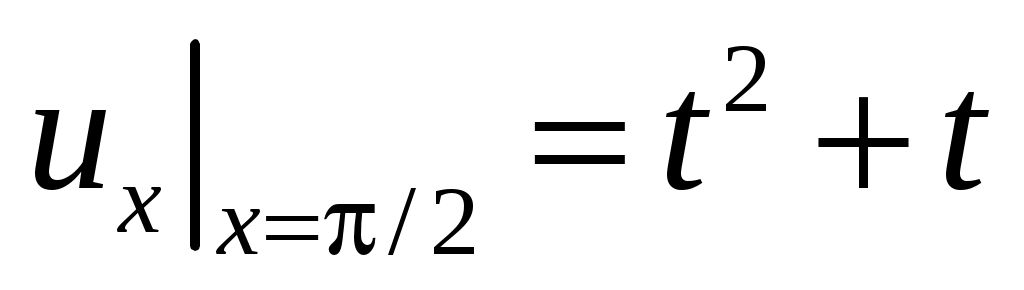 ,
, 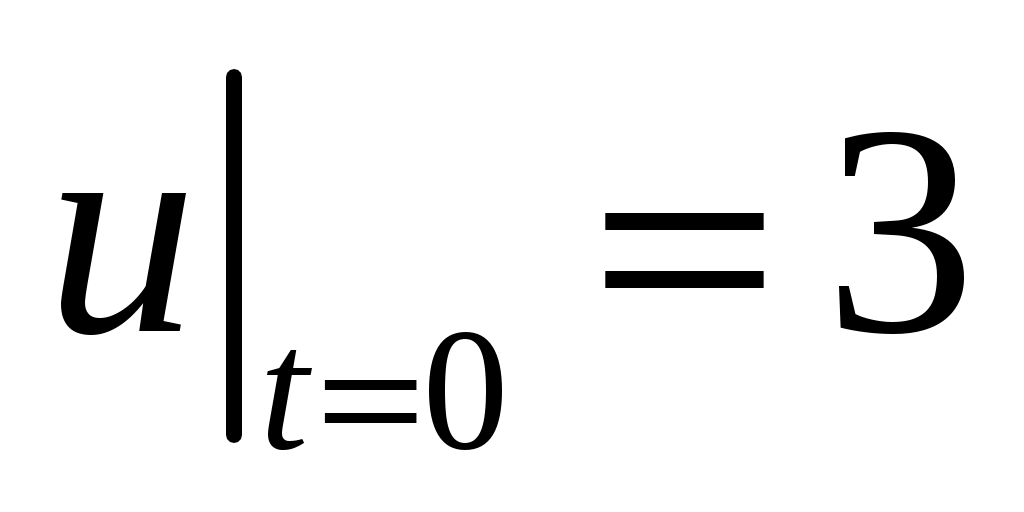 ,
, 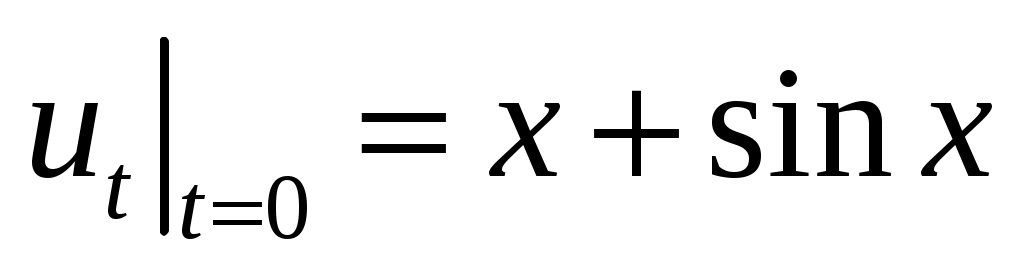 .
.
35.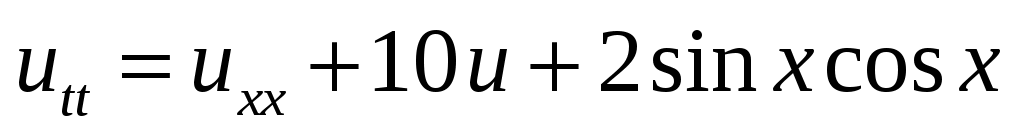 ,
,
 ,
, 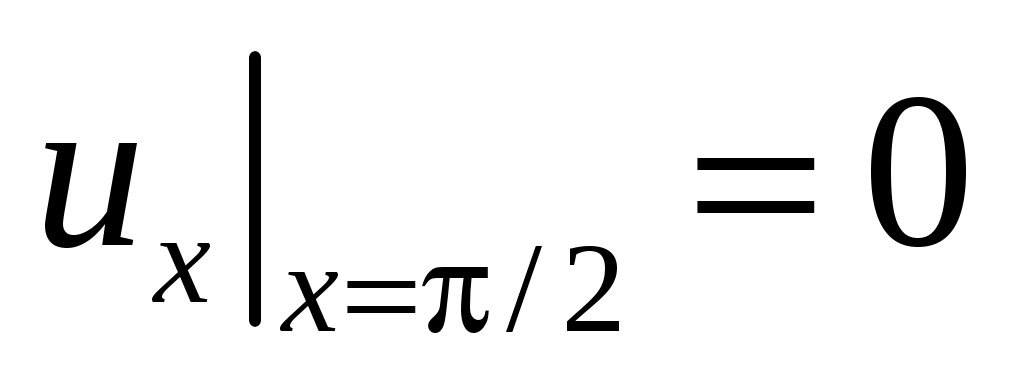 ,
,  .
.
Для домашних заданий удобно использовать богатый набор однотипных нетрудных задач из сборника [5], глава XI. Задачи для уравнения свободных колебаний струны с однородными ГУ полезно решать двумя способами: методом отражений и методом Фурье и сравнивать результаты.
Библиографический список
1. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики. 2-е изд. М., 1985.
2. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. 3-е изд. М., 1980.
3. Владимиров В.С. и др. Сборник задач по уравнениям математической физики. М., 2003.
4. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике. 13-е изд. СПб., М., 2003.
5. Кузнецов Л.А. Сборник заданий по высшей математике. М., 1994.
6. Очан Ю.С. Сборник задач по методам математической физики. 2-е изд. М., 1973.
7. Смирнов В.И. Курс высшей математики. Т.2. 21-е изд. М., 1974.
8. Смирнов М.М. Задачи по уравнениям математической физики. 6-е изд. М., 1975.
9. Тихонов А.Н., Самарский А.А. Уравнения математической физики. 5-е изд. М., 1977.
О г л а в л е н и е
Введение 4
§1. Вывод уравнения колебаний струны, постановка задач 5
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера* 12
§3. Корректность задач математической физики. Пример некорректной задачи 18
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений) 19
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений) 24
§6. Свободные колебания ограниченной струны. Метод Фурье (метод разделения переменных) 29
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных) 34
Задачи 39
Рыбакина Елена Альбертовна
Начально-краевые задачи
математической физики
Редактор Г.М.Звягина
Подписано в печать 07.06.2005. Формат бумаги 60х84/16. Бумага документная.
Печать трафаретная. Усл. печ.л. 3. Тираж 150 экз. Заказ №
Балтийский государственный технический университет
Типография БГТУ
190005, С-Петербург, 1-я Красноармейская ул., д.1
Пример 3. Решить вторую НКЗ для однородного уравнения струны:
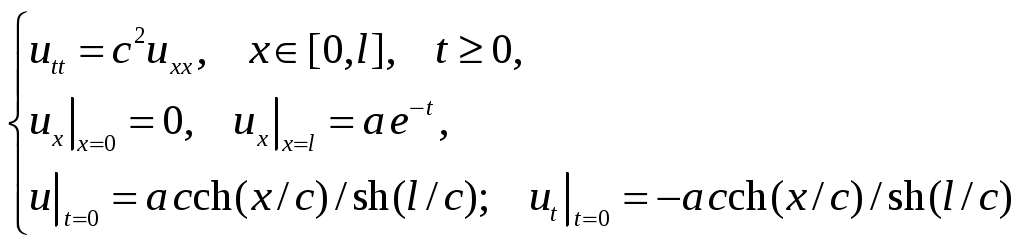
Решение задачи будем искать в виде суммы (50):
Подставим сумму
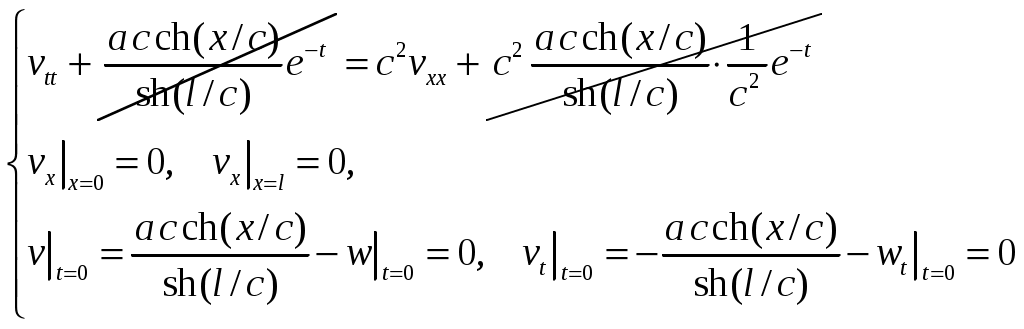
Для функции
уравнения с однородными НУ и ГУ, которая имеет только тривиальное решение:
.
Отметим, что в общем случае при таком методе решения для функции
20. Однородная струна со свободным концом
21. Однородная струна, закрепленная на конце
22. Однородная струна, свободная на конце
23. Описать продольные колебания цилиндрического стержня,
один конец которого свободен, а к другому с момента
24. На струну длиной l действует внешняя возмущающая сила, плотность которой равна
В задачах 25 – 28 функция
25.
26.
27.
.
28.
В задачах 29–32 функция
29.
30.
31.
32.
В задачах 33–35 функция
33.
,
34.
35.
Для домашних заданий удобно использовать богатый набор однотипных нетрудных задач из сборника [5], глава XI. Задачи для уравнения свободных колебаний струны с однородными ГУ полезно решать двумя способами: методом отражений и методом Фурье и сравнивать результаты.
Библиографический список
1. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики. 2-е изд. М., 1985.
2. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. 3-е изд. М., 1980.
3. Владимиров В.С. и др. Сборник задач по уравнениям математической физики. М., 2003.
4. Гюнтер Н.М., Кузьмин Р.О. Сборник задач по высшей математике. 13-е изд. СПб., М., 2003.
5. Кузнецов Л.А. Сборник заданий по высшей математике. М., 1994.
6. Очан Ю.С. Сборник задач по методам математической физики. 2-е изд. М., 1973.
7. Смирнов В.И. Курс высшей математики. Т.2. 21-е изд. М., 1974.
8. Смирнов М.М. Задачи по уравнениям математической физики. 6-е изд. М., 1975.
9. Тихонов А.Н., Самарский А.А. Уравнения математической физики. 5-е изд. М., 1977.
О г л а в л е н и е
Введение 4
§1. Вывод уравнения колебаний струны, постановка задач 5
§2. Задача Коши для свободных колебаний бесконечной струны. Формула Даламбера* 12
§3. Корректность задач математической физики. Пример некорректной задачи 18
§4. Свободные колебания полубесконечной струны. Метод отражений (метод продолжений) 19
§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений) 24
§6. Свободные колебания ограниченной струны. Метод Фурье (метод разделения переменных) 29
§7. Вынужденные колебания ограниченной струны. Метод Фурье (метод разделения переменных) 34
Задачи 39
Рыбакина Елена Альбертовна
Начально-краевые задачи
математической физики
Редактор Г.М.Звягина
Подписано в печать 07.06.2005. Формат бумаги 60х84/16. Бумага документная.
Печать трафаретная. Усл. печ.л. 3. Тираж 150 экз. Заказ №
Балтийский государственный технический университет
Типография БГТУ
190005, С-Петербург, 1-я Красноармейская ул., д.1