Файл: Упр 1 Приведите примеры технических устройств, действие которых основано на открытии радиоактивности, электромагнитных волн, ультразвука, реактивного движения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 147

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Упр81. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяженияв момент, когда расстояние между их центрами масс уменьшилось до 100 м.Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения. 2. На каком расстоянии от поверхности Марса сила взаимодействия меж-планетной станции Маринер-9 массой 1000 кг с планетой была равна1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 кмВ ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км. 3. Среднее расстояние между центрами Земли и Луны равно 60 земнымрадиусам, а масса Луны в 81 раз меньше массы Земли. В какой точкепрямой, соединяющей их центры, следует поместить тело, чтобы онопритягивалось к Земле и Луне с одинаковыми силами? 4. Определите силу притяжения шарика массой m и однородного шара,внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).Радиус шара R, масса M, расстояние между центрами тяжести LМасса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]. 6. Определите потенциал гравитационного поля на геостационарной орбитеЗемли. Какой потенциальной энергией обладает космический аппаратспутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли6 ∙ 10 24 кг, радиус Земли 6400 кмопределите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т. 7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.Радиус Земли R 3 >> H. Определите период обращения спутника. Орбитусчитайте круговойm*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2w^2=g*(Ro)^2/(Ro+H)^3w=корень(g*(Ro)^2/(Ro+H)^3)T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))если Ro >> HT=2*pi*корень((Ro+H)^3/(g*(Ro)^2)) 2*pi*корень(Ro^3/(g*(Ro)^2)) == 2*pi*корень(Ro/g) 2*3,14*корень(6400000/9,81) сек  5072 сек 84,5 мин

Ветер дует перпендикулярно стене. Плотность воздуха 1,29 кг/м 3p = 200 Паρ = 1,29 кг/м³_________v - ?F*Δt = 2*m*vm=ρ*V    (здесь V - объем, не путать с v - скоростью!!! :)F*Δt = 2*ρ*V*v              (1)Займемся объемом воздуха:V = S*L = S*v*Δt            (2) (S - площадь стены, L - путь, который воздух со  скоростью v пройдет за Δt секунд.Подставляя (2) в (1) получаем:F = 2*ρ*S*v²                   (3)Но сила давленияF = p*S                           (4)Опять приравниваем (4) и (3) и сокращаем на площадь стены:p = 2*ρ*v²Отсюда скорость:v = √ (p / (2·ρ) = √ (200 / (2·1,29) ≈ 8,5 м/с2. Определите силу давления ураганного ветра на стену дома высотой 30 ми длиной 50 м. Скорость ветра достигает 40 м/с и направлена под углом30° к стене. Сравните давление ветра с атмосферным давлением. Примитепоток воздуха вблизи стены ламинарным. упр 151. В широкой части горизонтальной трубы вода течет со скоростью 8 см/спри давлении, равном 1,5·10 5 Па. В узкой части трубы давление равно1,4·10 5 Па. Определите скорость течения в узкой части трубы без учетатрения.Для горизонтально расположенной трубы уравнение Бернулли записывается:rv1(2)/2+p1=rv2(2)/2+p2v2(2)=rv1(2)/2+p1-p2/(r/2)==1000кг/м3*(0.08м\с))*(0.08м\с)/2+1.5*10(5)Па-1.4*10(5)Па/1000кг\м3/2=4.47м\с2. В широкой части трубы нефть течет со скоростью 2 м/с. Определитескорость течения нефти в узкой части трубы, если разность давленийв широкой и узкой части трубы составляет 50 мм рт. СтУравнение: Р1+рgh1+рv1^2/2=Р2+рgh2+рv2^2/2. Здесь h1=h2, Р1-Р2=50мм. рт. ст. =

Определите внутреннюю энергию одноатом- ного идеального газа, взятого в количестве 5 молей, при температуре 27 °С? U = i/2*v*R*Ti=3 - для одноатомного газаv = 5 мольT=273+27=300 КU = i/2*v*R*T = 3/2 * 5 * 8,31 * 300 Дж = 18 698 Дж 18,7 КДж Зависит ли изменение внутренней энергии газа от способа его перевода из состояния 1 в состо- яние 2 (рис. 119)? Найдите изменение внутренней энергии при переходе из состояния 1 в состояние 2, если газ одноатомный; p0 = 105Па, V0 = 2 л. p1=3*10^4 Па V1=4 м3 р2=6*10^4 Па V2=12 м3 ΔU=?ΔU=(i/2)*v*R*ΔT Для 2-х атомных газов i=5Работа газа A=(p1+p2)*(V2-V1)/2=v*R*ΔT (графически - работа равна площади трапеции).ΔU=(5/4)*p1+p2)*(V2-V1)=(5/4)*(6+3)*(12-4)*10^4=0,9*10^6 Дж Один моль газа, имевший начальную температуру Т = 300 К, изобарно расширился, совершив работу А = 12,5·103 Дж. Во сколько раз при этом увеличится объем газа?

Плоский конденсатор с размером пластин 25 × 25 см и расстоянием между ними 0,5 мм заряжен от источника напряжения до разности потенциалов 10 В и отключен от источника. Какова будет разность потенциалов, если пластины конденсатора раздвинуть на расстояние 5 мм? Имеются три различных конденсатора. Электроемкость одного из них 2 мкФ. Когда все три конденсатора соединены последовательно, электро­ емкость соединения равна 1 мкФ. Когда конденсаторы соединены парал­ лельно, то электроемкость цепи 11 мкФ. Определите электроемкость двух неизвестных конденсаторов. Подставим численные значения: С2 = 3 Ф; С3 = 6 Ф или С2 = 6 Ф; С3 = 3 Ф. Электрическая схема, состоящая из двух последовательно соединенных незаряженных конденсаторов электроемкостью 1 мкФ и 3 мкФ, присоеди­ нена к источнику постоянного напряжения 220 В. Определите напряжение на каждом конденсаторе сразу после их подключения. Упр 35 Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора? Дано:C=20 мкФ;q=5 мкКл;_________Найти: WСИ: C=2*10⁻⁵ Ф; q=5*10⁻⁶ КлРешение:Воспользуемся формулой для энергии заряженного конденсатора: Выполним подстановку и расчет:  Дж или 625 нДжОтвет: 625 нДж. Электроемкость конденсатора, подключенного к источнику постоянного напряжения U = 1000 В, равна С1 = 5 пФ. Расстояние между его обклад­ ками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл. Изменение энергии электрического поля Пластины воздушного конденсатора отсоединили от источника тока, раздвинули вдвое и заполнили зазор диэлектриком с диэлектрической проницаемостью, равной 4. Во сколько раз уменьшилась энергия электрического поля в конденсаторе? Конденсатор отсоединенФормула для энергииW= q^2/ 2CC1= e0S/d былоC2= 4e0S/2d= 2C1 сталоЕмкость увеличилась в 2 разаЭнергия уменьшилась в 2 разаОтвет уменьшилась в 2 раза Пластины плоского конденсатора, площадью 200 см² каждая, располо­ жены на расстоянии 1 см. Какова энергия поля, если его напряженность 500 кВ/м? Дано: Найти W.Решение. Ответ: W = 220 мкДж Конденсатору электроемкостью 2 мкФ сообщен заряд 10–3 Кл. Обкладки конденсатора соединили проводником. Определите количество теплоты, выделившееся в проводнике при разрядке конденсатора, и разность потенциалов между обкладками до и после разрядки. Упр 36 Через нить лампочки карманного фонаря за время t = 2 мин проходит  заряд q1 = 20 Кл. Определите силу тока и время, за которое через нить  лампочки пройдет заряд q2 = 60 Кл. Решение: I =  I = =   А Если за 2 мин проходит заряд q₁ = 20 Кл, то q₂ = 60 Кл пройдёт за 2 · 3 = 6 мин.  Чему равно удельное сопротивление ρ проводника, если при силе тока I = 1 А падение  напряжения на нем U = 1,2 B? Диаметр  проводника d = 0,5 мм, длина l = 47 мм. R=U/I=1,2/1=1,2 ОмR=p*L/sp=R*s/L   s=pi*D^2/4=3,14*0,25*10^-6/4=0,2*10^-6 м^2p=1,2*0,2*10^-6/4,5=5,3*10^-8 Ом*м Есть четыре резистора одинакового сопротивления R = 10 Ом. Сколько существует  способов их соединения? Определите эквивалентное сопротивление в каждом случае. Последовательное или параллельное соединение. При последовательном соединении их общее сопротивление будет равно 40 Ом. При параллельном соединении их общее сопротивление будет равно 2,5 Ом.Формулы для расчета: Последовательное соединение резисторов Rобщ =  R1 + R2 + R3 + R4Параллельное соединение резисторов 1/Rобщ = 1/R1 + 1/R2 + 1/R3 + 1/R4.  Определите общее сопротивление цепи, изображенной на рисунке 200, если R = 4 Ом.R1=6 ом, r2=12 om, r3=5 om, r4=4om, r5=2 om, r6=4 om.1/R1,2=1/6+1/12=1/4R1,2=4 Ом1/R4,5,6=1/4+1/2+1/4=1R4,5,6=1 ОмR=R1,2+R3+R4,5,6R=4+5+1=10 ОмОтвет: общее сопротивление 10 Ом.Упр 37 Конденсатор емкостью С = 100 мкФ, заряженный до напряжения U = 300 B  разряжается за время Δt = 0,1 с. Определите среднее значение силы тока  при разряде конденсатора. Uo=300 BC1=50 мкФC2=100 мкФ-------------Q2 - ?РЕШЕНИЕопределим начальный зарядQo=Uo*C1 = 300 *50*10^-6 =0.015 Клпри параллельном соединении емкость системы   C=C1+C2=50 мкФ+100 мкФ=150 мкФтогда общее напряжение  U=U1=U2=Qo/C=0.015 Кл / 150*10^-6 Ф =100 Взаряд на C1    Q1= U1*C1=100 *50*10^-6 =0.005 Клзаряд на С2    Q2= U2*C2=100 *100*10^-6 =0.01 Кл Конденсатор емкостью 100 мкФ заряжается до напряжения 500 B за 0,5 с.  Каково среднее значение силы зарядного тока? Батарея аккумуляторов состоит из n = 8 элементов, соединенных последовательно. ЭДС каждого из элементов ε = 1,5 В, внутреннее сопротивление  r = 0,25 Ом. Внешнюю цепь образуют два параллельно соединенных  проводника сопротивлениями R1 = 10 Ом и R2 = 50 Ом. Определите напряжение на зажимах батареи. Задачу решим по закону Ома для полной цепи:  I=E/(R+r)ЭДС складывается из всех источников E = e*8 = 1,5*8 = 12 в.Внутреннее сопротивление r = 0,25 * 8 = 2 омПри параллельном сопротивлении R = R1*R2/(R1+R2)= 50*10/(50+10)=25/3 = 8⅓ омI = 12/(2+8⅓) = 1,16 aU = I*R = 1,16*8⅓ = 9,7 в Две группы из трех последовательно соединенных элементов соединены  параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Определите силу тока во внешней цепи. Ответ:Даноэпсилон=U=1,2Br=0,2OmR=1,5Omнайти: I-?Решение R=R/(R+r)=1,5/1,7



  1. В закрытом сосуде находится v = 4 моль аргона при температуре T = 300 K. На сколько процентов увеличится давление в сосуде, если газу сообщить количество теплоты Q = 900 Дж?

A=URT=4*8.31*300=9972ДЖ

N=A*100%/Q= 9%

  1. Один киломоль гелия расширяется изобарно. Температура газа увели- чивается на ΔT =30 K. Определите изменение внутренней энергии газа, совершенную им работу и количество теплоты, полученное газом.



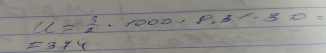
  1. Для изобарного нагревания газа от температуры T1 = 288 K до T2 = 340 K потребовалось количество теплоты Q = 5 кДж, для изохорного – Q = 3,56 кДж. Какой объем занимает газ при температуре 288 К и давлении р = 19,6 кПа?

Q1=5*10^3 Дж Q2=3.56*10^3 Дж Т1=288 К Т2=340 К р=19,6*10^3 Па V=?

==========

Изобарный

Q1=(i+2)*v*R*ΔT/2

Изохорный

Q2=(i/2)*v*R*ΔT

Q1/Q2=(i+2)/i

i=2/(Q1/Q2-1)=2/(5/3.56-1)=5

Газ двухатмный

v=2*Q1/(7*R*ΔT)

V=2*Q1*T1/(7*p*ΔT)=2*5*10^3*288/(7*19.6*10^3*(340-288))=0.4 м³

5. При адиабатном расширении газ совершил работу A = 400 Дж. Как и на сколько изменилась его внутренняя энергия?

Он сделал работу значит А=U

так как Формула изменени внутренняя энергия Q =A+U=400+400=800Дж

Упр 24

  1. Тепловая машина работает по замкнутому циклу. Подведенное за цикл количество теплоты Q1 = 0,1 МДж, отданное холодильнику – Q2 = 80 кДж. Определите полезную работу за цикл и КПД тепловой машины.

n=Q1-|Q2|:Q1
n=0.1*106 степени - 80*103степени : 0.1*106 степени =0.2 или 20%
А=0.2*0.1*106 степени = 20.000

  1. КПД автомобиля η = 22 %. Какое количество теплоты выделяется в камере сгорания двигателя автомобиля ежесекундно, если двигатель автомобиля развивает мощность N = 22,5 кВт?

кпд = A/Q*100% = P*t/Q*100%

Q = P*t/кпд*100% = 22500*1/22*100 Дж = 102272,7 Дж 102,3 кДж

  1. Определите КПД цикла, если известно, что максимальная и минимальная температуры в цикле отличаются в 3 раза (рис. 125). Рабочее тело – иде- альный одноатомный газ.

КПД = 1 - T2/T1
но Т1 = 4* Т2, то
КПД = 1 - Т2/Т1 = 1 - Т2/(4*Т2)= 1 - 1/4 = 3/4 или 75 %

5. Идеальная тепловая машина совершает за один цикл работу A = 73,5 кДж. Темпера- тура нагревателя t1 = 100 °C, температура холодильника t2 = 0 °C. Определите КПД цикла и количество теплоты, отданное за один цикл холодильнику.

Дано:

 

A = 73,5 кДж  = 73,5·103 Дж

Т1 = 100 °С = 373 К

Т2 = 0 °С = 273 К

η -? Q1 -? Q2 -?

Решение:

КПД идеальной тепловой машины



 



Количество теплоты Q1, получаемое машиной за один цикл от нагревателя


Количество теплоты Q2, отдаваемое за одни цикл холодильнику



Ответ: 





Упр 25

  1. Определите плотность насыщенных паров воды при температуре 50 °С.

    Дано:

     

    Т= 50 °С = 323 К

    р = 12,3 кПа = 13,3·103 Па

    μН2О = 18 ·10-3 кг/моль

    ρ  - ?




     

    Решение:

     

    Менделеева-Клапейрона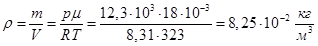



    Ответ: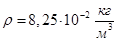 

  2. Насыщенный водяной пар, имевший начальную температуру 20 °С, отде­ лили от жидкости и нагрели до 30 °С при постоянном объеме. Определите давление пара. Как называют такой пар?

давление насыщенного пара р1 при температуре 20С=293К берем из таблицы р1=2328 Па. при изохорическом процессе p/T1=p2/T2, отсюда p2=p1(T2/T1)=2328*303/293=3122,5 Па. такой пар называют перегретым.

  1. Определите абсолютную влажность воздуха при температуре 50 °С, если давление водяного пара 8 кПа.





  1. Абсолютная влажность воздуха при температуре 300 К равна 12,9 г/м3. Чему равна относительная влажность воздуха?

Дано:

t=300K=27°

ρ=12.9г/м3

φ-?
Решение:

φ=ρ/ρ0*100%

ρ – плотность пара ρ0 – плотность насыщенного пара при данной температуре

φ –относительная влажность воздуха при данной температуре

Плотность насыщенного пара при температуре 27°С равна 25,8 г/м3 (табличное значение)Подставляем в формулу:

φ=12,9/25,8 *100% = 50%

Упр 26.

  1. Чему равен коэффициент поверхностного натяжения воды, если с помощью пипетки, имеющей кончик диаметром d = 0,4 мм, можно дози­ ровать воду с точностью до m = 0,01 г.

mg⃗ mg→ - сила тяжести и F⃗ F→ - сила поверхностного натяжения (рис.). Из условия равновесия капли найдем, что mg−F=0⇒F=mgmg−F=0⇒F=mg (*). Выразим силу поверхностного натяжения F=δl=δ2πRF=δl=δ2πR, где R=d/2R=d/2 - радиус кончика пипетки. После подстановки в формулу (*) получим: δπd=mg⇒δ=mg/πd=0,078Н/мδπd=mg⇒δ=mg/πd=0,078Н/м.

  1. Какую работу нужно совершить, чтобы выдуть мыльный пузырь радиусом R = 4 см?



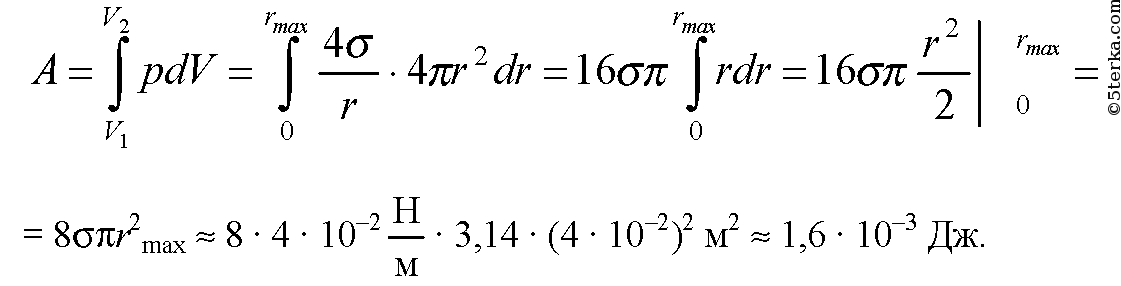
  1. Определите разность уровней ртути в двух сообщающихся капиллярах с диаметром каналов d = 1 мм и d = 2 мм.

d1 =1 мм = 1·10-3 м

d2=2 мм = 2·10-3 м H=h1-h2=4a/pgd1-4a/pgd2=7.5*10-23м
α = 0,5

ρ = 13,6·103 кг/м3

Δh - ?

Разность уровней

Упр 27

  1. Под действием какой силы, направленной вдоль оси стержня, в нем возни­ кает напряжение 15 107 2 × Í ì ? Диаметр стержня 0,40 см.



  1. Каково напряжение у основания кирпичной стены высотой 20 м? Одина­ ковой ли должна быть прочность кирпича у основания стены и в верхней ее части?





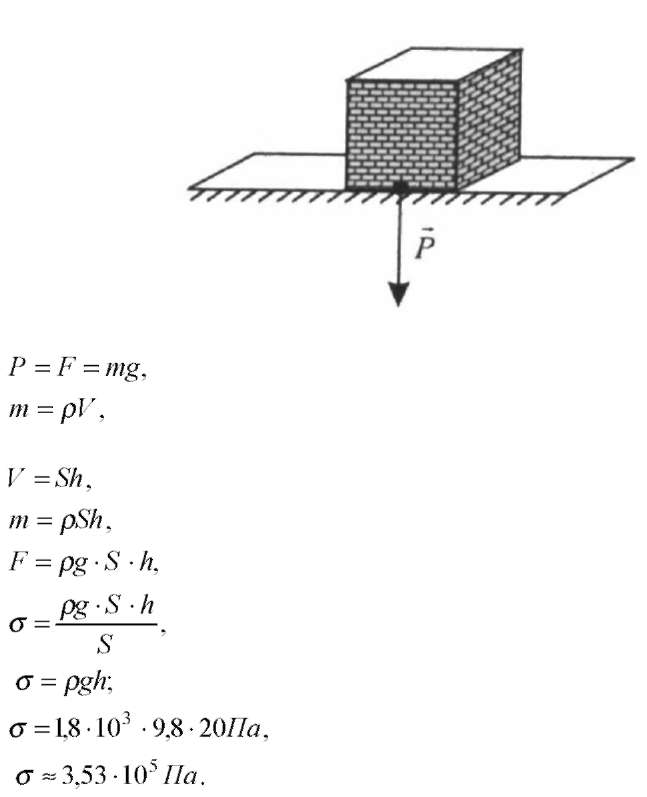
  1. Какую минимальную нагрузку должна испытать латунная проволока длиной 4,0 м и сечением 20 мм2, чтобы появилась остаточная деформация? Каким будет при этом относительное удлинение проволоки? Предел упру­ гости латуни sóïð Í ì =⋅ 11108 2 , . Массой проволоки можно пренебречь.



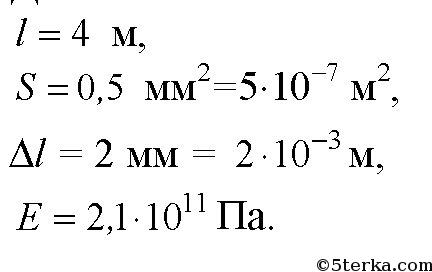
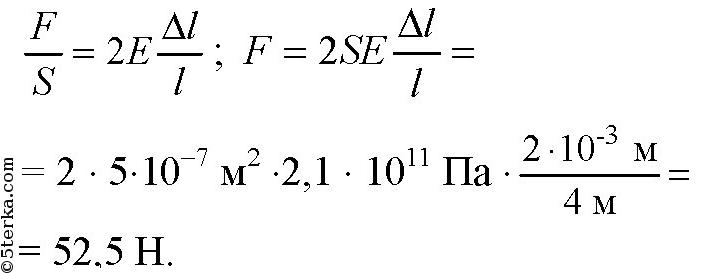
  1. Под действием силы в 100 Н проволока длиной 5,0 м и сечением 2,5 мм2 удлинилась на 1,0 мм. Определите напряжение, испытываемое прово­ локой, и модуль Юнга.





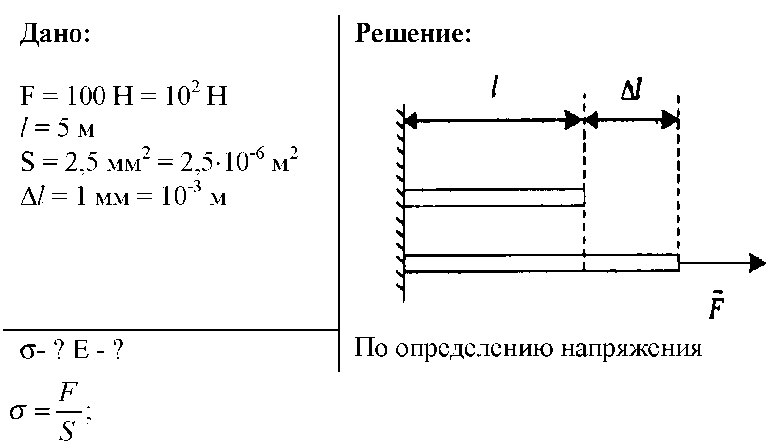
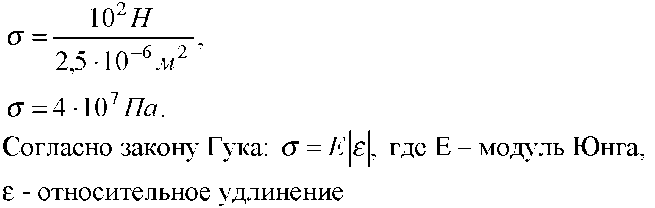
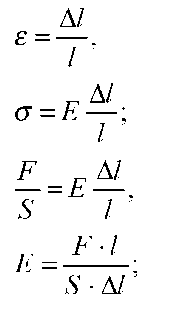
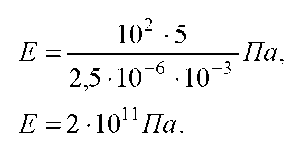
5. Какое сечение должен иметь медный стержень длиной 5,0 м, чтобы при нагрузке 480 Н он удлинился не более чем на 1,0 мм? Выдержит ли стер­ жень такое напряжение, если предел прочности меди при растяжении 2,2·108 Н/м2? Массу стержня не учитывать.

F/s=E*dL/L0
s=F*L0/E*dL=480*5/1,2*10^11*10^-3=2*10^-5 м2

Упр 28

  1. С какой силой взаимодействуют два точечных заряда 10 нКл и 15 нКл, находящиеся на расстоянии 5 см друг от друга?





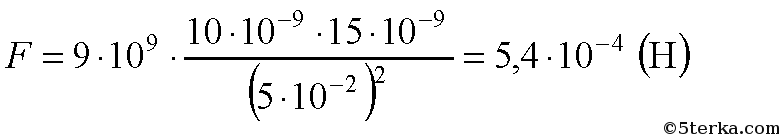
  1. Два одинаковых точечных заряда, находясь друг от друга на расстоянии 5 см, взаимодействуют силой 0,4 мН. Чему равен каждый из этих зарядов?

Дано: СИ

F = 0,4 мН 0,4*10⁻³ Н

q₁ = q₂ = q

r = 5 см 5*10⁻² м

_________

q - ?

Решение:

F = k*q*q / r²

q = r*√ (F/k)

q = 5*10⁻²*(√ ( 0,4*10⁻³/9*10⁹) ≈ 1*10⁻⁸ Кл

  1. Два одинаковых шарика, заряженные один положительным зарядом 15 мкКл, другой отрицательным –25 мкКл, приводят в соприкосновение и вновь раздвигают на расстояние 10 см. Определите заряд каждого шарика и силу их взаимодействия после соприкосновения.



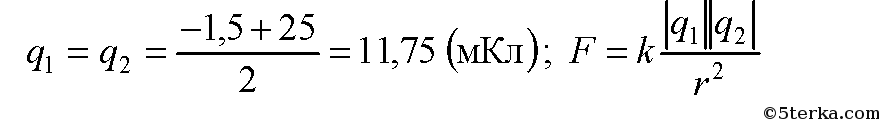
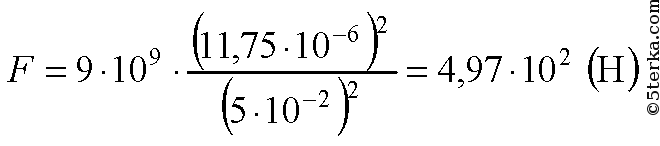
4. На нити висит заряженный шарик массой 20 г. Какой заряд q2 нужно поместить на расстояние 5 см от шарика, чтобы вес шарика уменьшился в 2 раза? Заряд шарика 10–6 Кл.

Смотрите также файлы