Файл: Упр 1 Приведите примеры технических устройств, действие которых основано на открытии радиоактивности, электромагнитных волн, ультразвука, реактивного движения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 146

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Упр81. Ракета-носитель массой 33 т приближаетсяк Международной космической станции массой 410 т. Определите силу притяженияв момент, когда расстояние между их центрами масс уменьшилось до 100 м.Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения. 2. На каком расстоянии от поверхности Марса сила взаимодействия меж-планетной станции Маринер-9 массой 1000 кг с планетой была равна1,78 кН? Масса Марса равна 6,4 ∙ 10 23 кг, радиус 3400 кмВ ычислите ускорение свободного падения тел вблизи поверхности Марса. Масса Марса равна 6⋅1023 кг, его радиус 3300 км. 3. Среднее расстояние между центрами Земли и Луны равно 60 земнымрадиусам, а масса Луны в 81 раз меньше массы Земли. В какой точкепрямой, соединяющей их центры, следует поместить тело, чтобы онопритягивалось к Земле и Луне с одинаковыми силами? 4. Определите силу притяжения шарика массой m и однородного шара,внутри которого есть сферическая плоскость радиусом R/2 (рис. 32).Радиус шара R, масса M, расстояние между центрами тяжести LМасса шара, который заполнил бы сферическую полость, равна Mпол=(4/3)πρ(R/2)3=M/8Mпол=(4/3)πρ(R/2)3=M/8, а центр его лежит на расстоянии r−R/2r−R/2 от шарика массы mm. Искомая сила, равная разности сил притяжения сплошного шара и меньшего шара, заполняющего сферическую полость, выразится так: F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]F=GMmr2−G(M/8)m(r−R/2)2=GMm[7r2−8rR+2R28r2(r−R/2)2]. 6. Определите потенциал гравитационного поля на геостационарной орбитеЗемли. Какой потенциальной энергией обладает космический аппаратспутниковой связи РК KazSat-3 массой 1,3 тонны на этой орбите (рис. 34).Расстояние от поверхности Земли до орбиты 36000 км. Масса Земли6 ∙ 10 24 кг, радиус Земли 6400 кмопределите кинетическую энергию космической станции при движении по орбите со скоростью 3,07 км/с, если масса станции 10 т. 7. Спутник движется вокруг Земли на расстоянии H от ее поверхности.Радиус Земли R 3 >> H. Определите период обращения спутника. Орбитусчитайте круговойm*a=mw^2*(Ro+H)=F=m*G*M/(Ro+H)^2=m*g*(Ro)^2/(Ro+H)^2mw^2*(Ro+H)=m*g*(Ro)^2/(Ro+H)^2w^2=g*(Ro)^2/(Ro+H)^3w=корень(g*(Ro)^2/(Ro+H)^3)T=2*pi/w=2*pi/корень(g*(Ro)^2/(Ro+H)^3)=2*pi*корень((Ro+H)^3/(g*(Ro)^2))если Ro >> HT=2*pi*корень((Ro+H)^3/(g*(Ro)^2)) 2*pi*корень(Ro^3/(g*(Ro)^2)) == 2*pi*корень(Ro/g) 2*3,14*корень(6400000/9,81) сек  5072 сек 84,5 мин

Ветер дует перпендикулярно стене. Плотность воздуха 1,29 кг/м 3p = 200 Паρ = 1,29 кг/м³_________v - ?F*Δt = 2*m*vm=ρ*V    (здесь V - объем, не путать с v - скоростью!!! :)F*Δt = 2*ρ*V*v              (1)Займемся объемом воздуха:V = S*L = S*v*Δt            (2) (S - площадь стены, L - путь, который воздух со  скоростью v пройдет за Δt секунд.Подставляя (2) в (1) получаем:F = 2*ρ*S*v²                   (3)Но сила давленияF = p*S                           (4)Опять приравниваем (4) и (3) и сокращаем на площадь стены:p = 2*ρ*v²Отсюда скорость:v = √ (p / (2·ρ) = √ (200 / (2·1,29) ≈ 8,5 м/с2. Определите силу давления ураганного ветра на стену дома высотой 30 ми длиной 50 м. Скорость ветра достигает 40 м/с и направлена под углом30° к стене. Сравните давление ветра с атмосферным давлением. Примитепоток воздуха вблизи стены ламинарным. упр 151. В широкой части горизонтальной трубы вода течет со скоростью 8 см/спри давлении, равном 1,5·10 5 Па. В узкой части трубы давление равно1,4·10 5 Па. Определите скорость течения в узкой части трубы без учетатрения.Для горизонтально расположенной трубы уравнение Бернулли записывается:rv1(2)/2+p1=rv2(2)/2+p2v2(2)=rv1(2)/2+p1-p2/(r/2)==1000кг/м3*(0.08м\с))*(0.08м\с)/2+1.5*10(5)Па-1.4*10(5)Па/1000кг\м3/2=4.47м\с2. В широкой части трубы нефть течет со скоростью 2 м/с. Определитескорость течения нефти в узкой части трубы, если разность давленийв широкой и узкой части трубы составляет 50 мм рт. СтУравнение: Р1+рgh1+рv1^2/2=Р2+рgh2+рv2^2/2. Здесь h1=h2, Р1-Р2=50мм. рт. ст. =

Определите внутреннюю энергию одноатом- ного идеального газа, взятого в количестве 5 молей, при температуре 27 °С? U = i/2*v*R*Ti=3 - для одноатомного газаv = 5 мольT=273+27=300 КU = i/2*v*R*T = 3/2 * 5 * 8,31 * 300 Дж = 18 698 Дж 18,7 КДж Зависит ли изменение внутренней энергии газа от способа его перевода из состояния 1 в состо- яние 2 (рис. 119)? Найдите изменение внутренней энергии при переходе из состояния 1 в состояние 2, если газ одноатомный; p0 = 105Па, V0 = 2 л. p1=3*10^4 Па V1=4 м3 р2=6*10^4 Па V2=12 м3 ΔU=?ΔU=(i/2)*v*R*ΔT Для 2-х атомных газов i=5Работа газа A=(p1+p2)*(V2-V1)/2=v*R*ΔT (графически - работа равна площади трапеции).ΔU=(5/4)*p1+p2)*(V2-V1)=(5/4)*(6+3)*(12-4)*10^4=0,9*10^6 Дж Один моль газа, имевший начальную температуру Т = 300 К, изобарно расширился, совершив работу А = 12,5·103 Дж. Во сколько раз при этом увеличится объем газа?

Плоский конденсатор с размером пластин 25 × 25 см и расстоянием между ними 0,5 мм заряжен от источника напряжения до разности потенциалов 10 В и отключен от источника. Какова будет разность потенциалов, если пластины конденсатора раздвинуть на расстояние 5 мм? Имеются три различных конденсатора. Электроемкость одного из них 2 мкФ. Когда все три конденсатора соединены последовательно, электро­ емкость соединения равна 1 мкФ. Когда конденсаторы соединены парал­ лельно, то электроемкость цепи 11 мкФ. Определите электроемкость двух неизвестных конденсаторов. Подставим численные значения: С2 = 3 Ф; С3 = 6 Ф или С2 = 6 Ф; С3 = 3 Ф. Электрическая схема, состоящая из двух последовательно соединенных незаряженных конденсаторов электроемкостью 1 мкФ и 3 мкФ, присоеди­ нена к источнику постоянного напряжения 220 В. Определите напряжение на каждом конденсаторе сразу после их подключения. Упр 35 Конденсатору емкостью 20 мкФ сообщили заряд 5 мкКл. Какова энергия заряженного конденсатора? Дано:C=20 мкФ;q=5 мкКл;_________Найти: WСИ: C=2*10⁻⁵ Ф; q=5*10⁻⁶ КлРешение:Воспользуемся формулой для энергии заряженного конденсатора: Выполним подстановку и расчет:  Дж или 625 нДжОтвет: 625 нДж. Электроемкость конденсатора, подключенного к источнику постоянного напряжения U = 1000 В, равна С1 = 5 пФ. Расстояние между его обклад­ ками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл. Изменение энергии электрического поля Пластины воздушного конденсатора отсоединили от источника тока, раздвинули вдвое и заполнили зазор диэлектриком с диэлектрической проницаемостью, равной 4. Во сколько раз уменьшилась энергия электрического поля в конденсаторе? Конденсатор отсоединенФормула для энергииW= q^2/ 2CC1= e0S/d былоC2= 4e0S/2d= 2C1 сталоЕмкость увеличилась в 2 разаЭнергия уменьшилась в 2 разаОтвет уменьшилась в 2 раза Пластины плоского конденсатора, площадью 200 см² каждая, располо­ жены на расстоянии 1 см. Какова энергия поля, если его напряженность 500 кВ/м? Дано: Найти W.Решение. Ответ: W = 220 мкДж Конденсатору электроемкостью 2 мкФ сообщен заряд 10–3 Кл. Обкладки конденсатора соединили проводником. Определите количество теплоты, выделившееся в проводнике при разрядке конденсатора, и разность потенциалов между обкладками до и после разрядки. Упр 36 Через нить лампочки карманного фонаря за время t = 2 мин проходит  заряд q1 = 20 Кл. Определите силу тока и время, за которое через нить  лампочки пройдет заряд q2 = 60 Кл. Решение: I =  I = =   А Если за 2 мин проходит заряд q₁ = 20 Кл, то q₂ = 60 Кл пройдёт за 2 · 3 = 6 мин.  Чему равно удельное сопротивление ρ проводника, если при силе тока I = 1 А падение  напряжения на нем U = 1,2 B? Диаметр  проводника d = 0,5 мм, длина l = 47 мм. R=U/I=1,2/1=1,2 ОмR=p*L/sp=R*s/L   s=pi*D^2/4=3,14*0,25*10^-6/4=0,2*10^-6 м^2p=1,2*0,2*10^-6/4,5=5,3*10^-8 Ом*м Есть четыре резистора одинакового сопротивления R = 10 Ом. Сколько существует  способов их соединения? Определите эквивалентное сопротивление в каждом случае. Последовательное или параллельное соединение. При последовательном соединении их общее сопротивление будет равно 40 Ом. При параллельном соединении их общее сопротивление будет равно 2,5 Ом.Формулы для расчета: Последовательное соединение резисторов Rобщ =  R1 + R2 + R3 + R4Параллельное соединение резисторов 1/Rобщ = 1/R1 + 1/R2 + 1/R3 + 1/R4.  Определите общее сопротивление цепи, изображенной на рисунке 200, если R = 4 Ом.R1=6 ом, r2=12 om, r3=5 om, r4=4om, r5=2 om, r6=4 om.1/R1,2=1/6+1/12=1/4R1,2=4 Ом1/R4,5,6=1/4+1/2+1/4=1R4,5,6=1 ОмR=R1,2+R3+R4,5,6R=4+5+1=10 ОмОтвет: общее сопротивление 10 Ом.Упр 37 Конденсатор емкостью С = 100 мкФ, заряженный до напряжения U = 300 B  разряжается за время Δt = 0,1 с. Определите среднее значение силы тока  при разряде конденсатора. Uo=300 BC1=50 мкФC2=100 мкФ-------------Q2 - ?РЕШЕНИЕопределим начальный зарядQo=Uo*C1 = 300 *50*10^-6 =0.015 Клпри параллельном соединении емкость системы   C=C1+C2=50 мкФ+100 мкФ=150 мкФтогда общее напряжение  U=U1=U2=Qo/C=0.015 Кл / 150*10^-6 Ф =100 Взаряд на C1    Q1= U1*C1=100 *50*10^-6 =0.005 Клзаряд на С2    Q2= U2*C2=100 *100*10^-6 =0.01 Кл Конденсатор емкостью 100 мкФ заряжается до напряжения 500 B за 0,5 с.  Каково среднее значение силы зарядного тока? Батарея аккумуляторов состоит из n = 8 элементов, соединенных последовательно. ЭДС каждого из элементов ε = 1,5 В, внутреннее сопротивление  r = 0,25 Ом. Внешнюю цепь образуют два параллельно соединенных  проводника сопротивлениями R1 = 10 Ом и R2 = 50 Ом. Определите напряжение на зажимах батареи. Задачу решим по закону Ома для полной цепи:  I=E/(R+r)ЭДС складывается из всех источников E = e*8 = 1,5*8 = 12 в.Внутреннее сопротивление r = 0,25 * 8 = 2 омПри параллельном сопротивлении R = R1*R2/(R1+R2)= 50*10/(50+10)=25/3 = 8⅓ омI = 12/(2+8⅓) = 1,16 aU = I*R = 1,16*8⅓ = 9,7 в Две группы из трех последовательно соединенных элементов соединены  параллельно. ЭДС каждого элемента равна 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Определите силу тока во внешней цепи. Ответ:Даноэпсилон=U=1,2Br=0,2OmR=1,5Omнайти: I-?Решение R=R/(R+r)=1,5/1,7



k=9*10^9

m=29*10^-3

r=5*10^-2

q1=2*10^-6

q2=?

k*q1*12/r²=m*g/2

q2=(m*g*r²)/(k*q1)=...............

осталось подставить и сосчитать.

5. Два маленьких шарика одинаковой массы, каждому из которых сообщили заряд 9·10–7 Кл, подвешены на нитях длинной 1 м. Угол, на который они разошлись, равен 60°. Определите массы шариков.

Два маленьких шарика одинаковой массы, каждому из которых сообщили заряд 4*10^-7 Кл, подвешены на нитях длиной 1 м. Угол, на который разошлись нити, равен 60 градусов. Определите массы шариков

Дано:

m₁=m₂;

q₁=q₂=4*10⁻⁷ Кл;

l=1 м;

α=60°;

_____________

Найти: m₁, m₂

Решение:

Система находится в равновесии, поэтому сумма всех сил, действующих на каждый шарик в отдельности равна нулю:



Распишем это равенство в проекциях на координатные оси:

Ох 

Oy 

Выразим силу натяжения нити из первого уравнения и подставим во второе:







Выполним подстановку и расчет (при этом учтем, что расстояние между зарядами равно l=1 м т.е. треугольник равносторонний):

 Н

 кг или 0,25 г

Упр 29

  1. С каким ускорением движется электрон в поле с напряженностью 10 В/м?



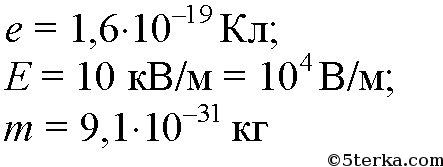
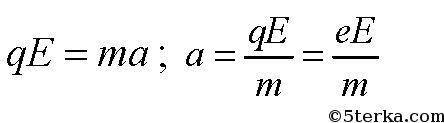
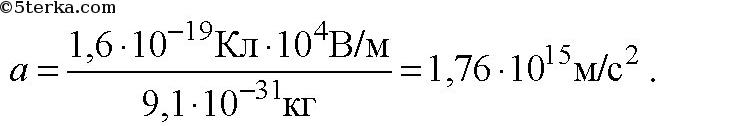
  1. Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Определите напряженность поля в точке, удаленной на 5 см от каждого из зарядов. Решить эту задачу для случаев: а) оба заряда положительные; б) один заряд положительный, другой – отрицательный.



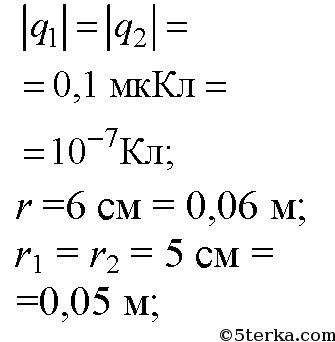
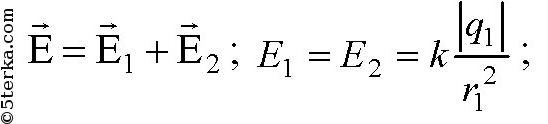
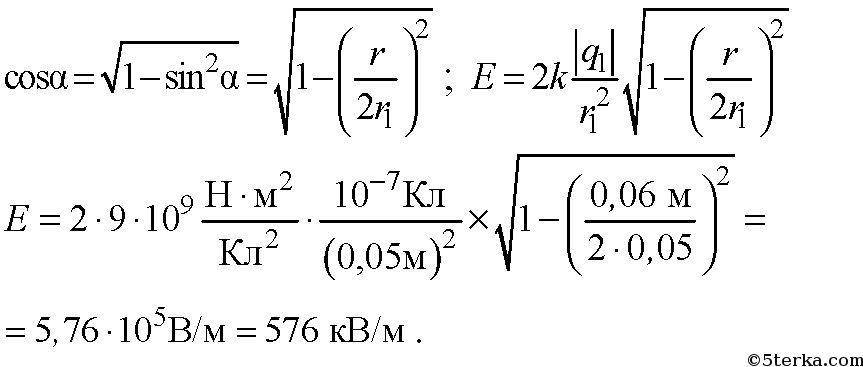
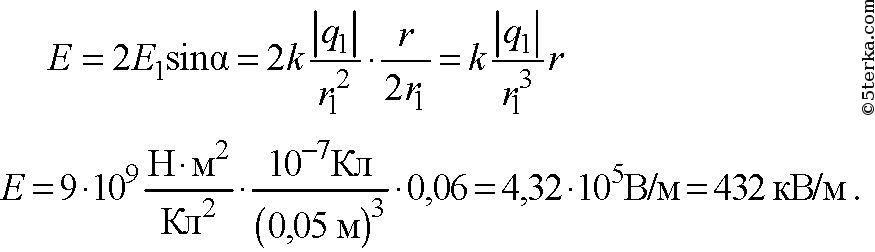
  1. Заряженный металлический шарик, подвешенный на шелковой нити, внесли в однородное электрическое поле. Нить отклонилась от вертикали на угол 45°. Как изменится угол отклонения нити при стекании с шарика 0,1 доли его заряда? Линии напряженности поля направлены горизонтально.





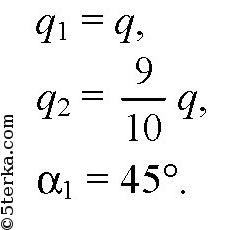
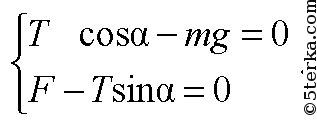
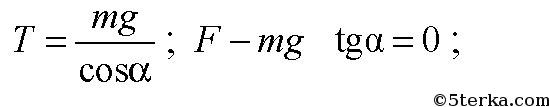
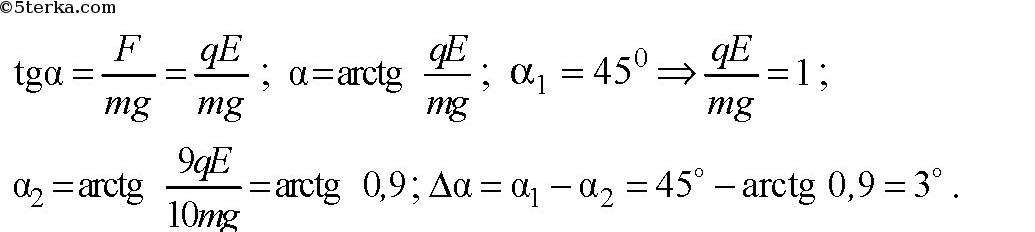
  1. Определите напряженность электрического поля в точке, удаленной от точеч­ ного заряда на 2 м, если на расстоянии, равном 20 см от него, напряженность поля равна 4·10–4 В/м. Определите также заряд, создающий поле.

Дано:

r₁ = 20 см = 0,20 м

E₁ = 4·10⁻⁴ В/м


r₂ = 2 м

____________

E₂ - ?

q - ?

Напряженность:E = k·q / r² Тогда:

E₂ / E₁ = (r₁/r₂)²

E₂ = E₁· (r₁/r₂)² = 4·10⁻⁴·(0,20/2) = 4·10⁻⁵ В/м

q = E₂·r²/k = 4·10⁻⁵·2²/(9·10⁹) ≈ 18·10⁻¹⁵  Кл
5. Три заряда q1 = q2 = 4·10–8 Кл и q3 = –8·10–8 Кл поместили в вершинах треугольника со стороной а = 30 см. Определите напряженность поля в центре треугольника.



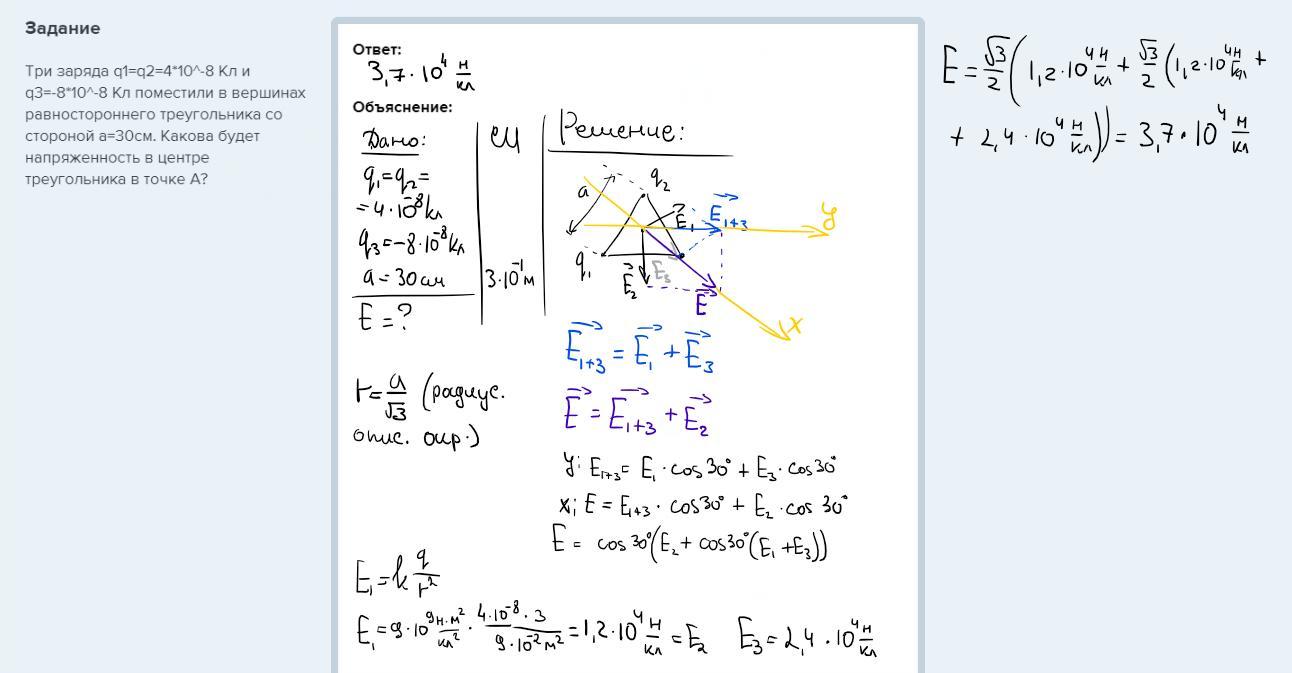
Упр 30

  1. Заряженный проводящий шар радиусом r расположен внутри металлической сетки (рис. 160), радиус которой равен R. Определите значение напряженности поля в точках A, В, C, удаленных от центра шара на расстояния RA, RB, RC. Поверхностные плотности зарядов на шаре и сетке равны σ.

ЧЕРЕЗ ТЕОРЕМУ ГАУССА:


для произвольной замкнутой поверхности окружающий некторый заряд;

Ясно, что поле вокруг такого тела обладает сферической симметрией, а значит поле в любой точке сонаправлено в радиус-вектором, проведённым из центра сферы. Причём, исходя из той же сферической симметри – на равных расстояниях от сферы в любой точке поле имеет одну и ту же напряжённость.

Поэтому для точек         за пределами шара мы можем записать:


А для точек         внутри шара мы можем записать:





ЧЕРЕЗ УДЕЛЬНУЮ ФОРМУ ЗАКОНА КУЛОНА ДЛЯ ШАРА:

Для точек         за пределами шара мы можем записать:




А для точек         внутри шара мы можем записать:




ЧЕРЕЗ УДЕЛЬНУЮ ФОРМУ ЗАКОНА КУЛОНА ДЛЯ СФЕРЫ:

Напряжённость равномерно заряженной сферы за её пределеами равна напряжённости точечного заряда, расположенного вместо сферы в её центре. Тогда:


Для точек         за пределами шара мы можем записать:



А для точек         внутри шара мы можем записать:



ОТВЕТ:


    при    
    при    

  1. Проводящая сфера радиусом R заряжена с поверх­ ностной плотностью заряда σ и окружена проводящей оболочкой, внутренний радиус которой равен R1, а внешний – R2. Определите зависимость напряжен­ ности поля от r радиуса и постройте график этой зависимости.

  2. Решение:








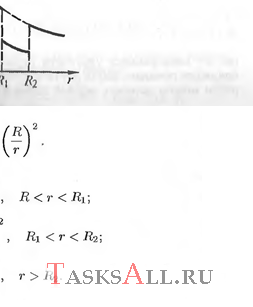  1. Две заряженные параллельные пластины имеют поверхностные плот­ ности –σ и + σ. Расстояние между пластинами d. Постройте кривую зависимости напряженности поля от координаты x, если ось 0x проведена перпендикулярно плоскости пластин.

Решение:








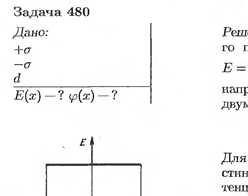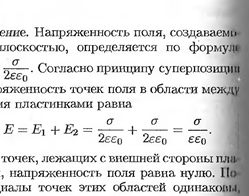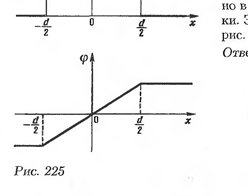  1. Напряженность поля вблизи большой заряженной пластины в ее центре E = 10 4 В/м. Линии напряженности направлены к пластине. Оцените поверхностную плотность зарядов на пластине, если она заряжена равно­ мерно.

u=i: r

r=r1+r2+r3+r4

r=184om

u=5: 184=0.027в
(30142+х): 876=49

30142+х=42924

х=12782



  1. На нити висит шарик массой m = 10 г и зарядом q = 10–6 Кл. Определите поверхностную плотность зарядов, переданных на горизонтальную пластину под шариком, если сила натяжения нити уменьшилась вдвое.

Дано:
 = 10 г = 0.01 кг
 Кл
 = 1000 Н/Кл = 10³ Н/Кл
 = 9.8 м/с² - ускорение свободного падения

Найти:
 

Решение:
Представим себе шарик, висящий на нитке, прикрепленной к потолку. Тогда, сила натяжения нити направлена вверх, то есть по направлению к потолку. В то же время на шарик действует сила тяжести  , направленная вниз и сила со стороны электрического поля  . Все три силы должны уравновешивать друг друга. Значит, сила натяжения нити будет максимальна, если будет уравновешивать силу тяжести и силу со стороны электрического поля (для этого сила электрического поля акже должна быть направлена вниз):
.
Осталось только вспомнить, как определяются эти силы и получить численное значение.



Можно округлить до 0.1 Н.

Ответ: 0.1 Н.

Упр 31

  1. Два точечных заряда q1 = 6,6·10–9 Кл и q2 = 1,32·10–8 Кл находятся на рас­ стоянии r1 = 40 см. Какую работу необходимо совершить, чтобы сблизить их до расстояния r2 = 25 см?

Дано: q1=6,6*10^-9 Кл  q2=1,32*10^-8 Кл  R=0,4 м  F?  

 F=k*q1*q2/R^2=9*10^9*6,6*10^-9*1,32*10^-8/0,16=4,9*10^-6 H

  1. Между двумя вертикальными пластинами, находящимися на расстоянии d = 1 см друг от друга, висит заряженный бузиновый шарик массой m = 0,1 г. После того как на пластины было подано напряжение, равное U = 1000 В, нить с шариком отклонилась на угол α = 10°. Определите заряд шарика q.

 
 

Смотрите также файлы