Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 294

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Программная реализация

Результаты

Часть 1: эллиптические кривые над вещественными числами и групповой закон

Эллиптические кривые

Группы

Групповой закон для эллиптических кривых

Геометрическое сложение

Алгебраическое сложение

Скалярное умножение

Логарифм

Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования

Поле целых чисел по модулю p

Эллиптические кривые над 

Сложение точек

Алгебраическая сумма

Порядок группы эллиптической кривой

Скалярное умножение и циклические подгруппы

Дискретный логарифм

Часть 3: ECDH и ECDSA

Параметры области определения

Криптография на эллиптических кривых

Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA

Взлом задачи дискретного логарифмирования

Baby-step, giant-step

ρ Полларда

Сравниние ρ Полларда и Baby-step giant-step

Дальнейшие рассуждения

Порядок группы эллиптической кривой



Мы сказали, что эллиптическая кривая, определённая над конечным полем, имеет конечное количество точек. Нам нужно ответить на важный вопрос: сколько же в ней точек?

Во-первых, давайте определим, что количество точек в группе называется порядком группы.

Проверка всех возможных значений для   в интервале от 0 до   будет невыполнимым способом подсчёта точек, потому что потребует   шагов, а эта задача «сложна», если   — большое простое число.

К счастью, для вычисления порядка существует более быстрый алгоритм: алгоритм Шуфа. Я не буду вдаваться в его подробности — главное, что он выполняется за полиномиальное время, а именно этого нам и нужно.

Скалярное умножение и циклические подгруппы



Для вещественных чисел умножение можно определить как:



И, повторюсь, мы можем использовать алгоритм удвоения-сложения для выполнения умножения за  , где   — это количество бит  ). Я написал интерактивный инструмент для скалярного умножения.

Умножение точек для эллиптических кривых над   обладает интересным свойством. Возьмём кривую   и точку  . Теперь вычислим все величины, кратные  :




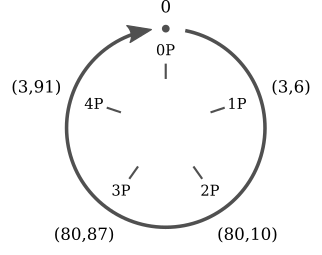
Все значения, кратные  , представляют собой пять различных точек ( ,  ,  ,  ,  ), которые циклически повторяются. Легко заметить сходство между скалярным умножением для эллиптических кривых и сложением в модулярной арифметике.






















  • ...


Можно сразу же заметить две особенности: во-первых, значений, кратных  , всего пять: другие точки эллиптической кривой никогда ими не становятся. Во-вторых, они повторяются циклически. Можно записать:













для любого целого  . Заметьте, что благодаря оператору деления с остатком эти пять уравнений можно «ужать» в одно:  .

Более того, мы можем сразу же показать, что эти пять точек замкнуты относительно операции сложения. Что это значит: как бы я ни суммировал  ,  ,  ,   или  , результатом всегда будет одна из этих пяти точек. И снова все остальные точки эллиптической кривой никогда не становятся результатом.


То же относится и ко всем остальным точкам, не только к  . На самом деле, если мы возьмём   в общем виде:



Что означает: если мы складываем два значения, кратных  , то получаем значение, кратное   (т.е. значения, кратные  , замкнуты относительно операции сложения). Этого достаточно для того, чтобы доказать, что множество кратных   значений — это циклическая подгруппа группы, образованной эллиптической кривой.

«Подгруппа» — это группа, являющаяся подмножеством другой группы. «Циклическая подгруппа» — это подгруппа, элементы которой циклически повторяются, как мы показали в предыдущем примере. Точка   называется генератором или базовой точкой циклической подгруппы.

Циклические подгруппы — фундамент для ECC и других криптосистем. Позже я объясню, почему это так.

Порядок подгруппы



Можно задаться вопросом, каков порядок подгруппы, порождённой точкой   (или, иными словами, каков порядок  ). Для ответа на этот вопрос мы не можем использовать алгоритм Шуфа, потому что этот алгоритм работает только для целых эллиптических кривых, но не для подгрупп. Прежде чем приступить к решению задачи, нам нужно ещё немного информации:


  • Пока мы определяли порядок как количество точек группы. Это определение по-прежнему действительно, но в циклических подгруппах мы можем дать новое аналогичное определение: порядок   — это минимальное положительное целое  , такое, что  .

    На самом деле, если посмотреть на предыдущий пример, то наша подгруппа состояла из пяти точек, и  .

  • Порядок   связан с порядком эллиптической кривой теоремой Лагранжа, согласно которой порядок подгруппы — это делитель порядка исходной группы.

    Иными словами, если эллиптическая кривая содержит   точек, а одна из подгрупп содержит  , то   является делителем  .


Два этих факта вместе дают нам возможность определить порядок подгруппы с базовой точкой  :


  1. Вычисляем порядок эллиптической кривой   с помощью алгоритма Шуфа.

  2. Находим все делители  .

  3. Для каждого делителя   порядка   вычисляем  .

  4. Наименьшее  , такое, что  , является порядком подгруппы.


Например, кривая   над полем   имеет порядок  . Её подгруппы могут иметь порядок  ,  ,  ,  ,  ,  ,   или  . Если мы подставим  , то увидим, что  ,  , ...,  , то есть порядок   равен  .

Учтите, что важно брать наименьший, а не случайный делитель. Если мы будем выбирать случайно, то можем получить  , что не является порядком подгруппы, но является одним из кратных.

Ещё один пример: эллиптическая кривая, определяемая уравнением   над полем  , имеет порядок  , которое является простым числом. Её подгруппы могут иметь порядок только   или  . Как вы можете догадаться, когда  , подгруппа содержит только бесконечно удалённую точку; когда  , подгруппа содержит все точки эллиптической кривой.


Поиск базовой точки



Для алгоритмов ECC требуются подгруппы с высоким порядком. Поэтому обычно выбирается эллиптическая кривая, вычисляется её порядок ( ), в качестве порядка группы ( ) выбирается большой делитель, а потом находится подходящая базовая точка. То есть мы не выбираем базовую точку, после чего вычисляем её порядок, а производим обратную операцию: сначала выбираем достаточно хороший порядок, а потом ищем подходящую базовую точку. Как же это сделать?

Во-первых, нужно ввести ещё одно понятие. Теорема Лагранжа подразумевает, что число   всегда целое (потому что   — делитель  ). Число   имеет собственное название: это кофактор подгруппы.

Теперь рассмотрим, что для каждой точки эллиптической кривой есть  . Это справедливо, потому что   — это кратное любому возможному  . Исходя из определения кофактора, мы можем записать:



Теперь допустим, что   — простое число (мы предпочитаем простые порядки по причинам, изложенным в первой части статьи). Это уравнение, записанное в такой форме, говорит нам, что точка   создаёт подгруппу порядка   (за исключением случая  , в котором подгруппа имеет порядок 1).

В свете этого мы можем определить следующий алгоритм:


  1. Вычисляем порядок   эллиптической кривой.

  2. Выбираем порядок   подгруппы. Чтобы алгоритм сработал, число должно быть простым и быть делителем  .

  3. Вычисляем кофактор  .

  4. Выбираем на кривой случайную точку  .

  5. Вычисляем  .

  6. Если   равно 0, то возвращаемся к шагу 4. В противном случае мы нашли генератор подгруппы с порядком   и кофактором  .

Смотрите также файлы