Файл: Разработка программного обеспечения алгоритма Диффи Хелмана на основе эллиптических кривых.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 300
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1: эллиптические кривые над вещественными числами и групповой закон
Групповой закон для эллиптических кривых
Часть 2: эллиптические кривые над конечными полями и задача дискретного логарифмирования
Порядок группы эллиптической кривой
Скалярное умножение и циклические подгруппы
Криптография на эллиптических кривых
Часть 4: алгоритмы для взлома защиты ECC и сравнение с RSA
Взлом задачи дискретного логарифмирования
Заметьте, что алгоритм работает только если
простое. Если бы не было простым, то порядок мог быть одним из делителей .Дискретный логарифм
Как и в случае с непрерывными эллиптическими кривыми, теперь мы должны обсудить следующий вопрос: если мы знаем
и , то каким будет , такое, что ?Эта задача, известная как задача дискретного логарифмирования для эллиптических кривых, считается «сложной», для которой не обнаружено алгоритма полиномиального времени, выполняемого на классическом компьютере. Однако у этой точки зрения нет математических доказательств.
Эта задача аналогична задаче дискретного логарифмирования, используемой в других криптосистемах, таких как Digital Signature Algorithm (DSA), протокол Диффи-Хеллмана (D-H) и схема Эль-Гамаля. Названия задач совпадают неслучайно. Их разница в том, что в этих алгоритмах используется не скалярное умножение, а возведение в степень по модулю. Их задачу дискретного логарифмирования можно сформулировать так: если известны
и , то каким будет , такое, что ?Обе эти задачи «дискретны», потому что в них используются конечные множества (а конкретнее — циклические подгруппы). И они являются «логарифмами», потому что аналогичны обычным логарифмам.
ECC интересна тем, что на сегодняшний момент задача дискретного логарифмирования для эллиптических кривых кажется «сложнее» по сравнению с другими схожими задачами, используемыми в криптографии. Это подразумевает, что нам потребуется меньше бит для целого
, чтобы получить тот же уровень защиты, что и в других криптосистемах, и мы это подробно рассмотрим в четвёртой, последней, части статьи.Часть 3: ECDH и ECDSA
Параметры области определения
Алгоритмы эллиптических кривых будут работать в циклической подгруппе эллиптической кривой над конечным полем. Поэтому алгоритмам потребуются следующие параметры:
-
Простое , задающее размер конечного поля. -
Коэффициенты и уравнения эллиптической кривой. -
Базовая точка , генерирующая подгруппу. -
Порядок подгруппы. -
Кофактор подгруппы.
В результате параметрами области определения для алгоритмов является шестёрка
.Случайные кривые
Когда я говорил, что задача дискретного логарифмирования «сложна», я был не совсем точен. Существуют определённые классы эллиптических кривых, которые довольно слабы и позволяют использовать специальные алгоритмы для эффективного решения задачи дискретного логарифмирования. Например, все кривые, для которых
(то есть порядок конечного поля равен порядку эллиптической кривой), уязвимы к атаке Смарта, которую можно использовать для решения дискретных логарифмов за полиномиальное время на классических компьютерах.Предположим теперь, что я дал вам параметры области определения кривой. Существует вероятность, что я обнаружил неизвестный никому новый класс слабых кривых, и, возможно, я создал «быстрый» алгоритм вычисления дискретных логарифмов для своей кривой. Как я могу убедить вас в обратном, т.е. в том, что мне неизвестно об уязвимостях? Как я могу гарантировать, что кривая «защищена» (в том смысле, что я не смогу её использовать для собственных атак)?
Чтобы решить эту проблему, иногда приходится использовать дополнительный параметр области определения:
порождающее значение (seed)
. Это случайное число, используемое для генерирования коэффициентов и или базовой точки , или того и другого. Эти параметры генерируются вычислением хеша . Хеши, как мы знаем, «просто» вычислить, но «сложно» реверсировать.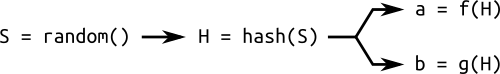
Простая схема генерирования случайной кривой из порождающего значения: хеш случайного числа используется для вычисления различных параметров кривой.
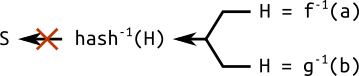
Если бы мы хотели сжульничать и воссоздать хеш из параметров области определения, то нам пришлось бы решать «сложную» задачу: инверсирование хеша.
Сгенерированная с помощью порождающего значения кривая называется проверяемо случайной. Принцип использования хешей для генерирования параметров известен как "nothing up my sleeve" («в рукавах ничего нет»), и широко распространён в криптографии.
Эта хитрость даёт определённую гарантию, что кривая не была специально создана таким образом, чтобы иметь известные её автору уязвимости. На самом деле, если я даю вам кривую вместе с порождающим значением, то это значит, что я не мог произвольно выбирать параметры
и , и можно быть относительно спокойным, что я не смогу использовать специальные атаки. Причина использования слова «относительно» будет объяснена в четвёртой части.Стандартизированный алгоритм генерирования и проверки случайных кривых описан в ANSI X9.62 и основан на SHA-1. Если интересно, можете прочитать об алгоритмах генерирования проверяемо случайных кривых в спецификации SECG (см. «Verifiably Random Curves and Base Point Generators»).
Я написал небольшой скрипт на Python
, проверяющий все случайные кривые, поставляемые сейчас с OpenSSL. Крайне рекомендую посмотреть его!