Файл: севастопольский государственный универитет морской институт.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 553
Скачиваний: 24
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2 Подбор соответсвующего прототипа и выбор основыных элементов и главных размерений
2.1 Алгебраическое кубическое уравнение масс
2.2 Выбор соотношений главных размерений и коэффициентов полноты проектируемого судна
4 Расчет нормальной шпации и разбивка корпуса на отсеки
6 Определение высоты надводного борта
7 Расчеты непотопляемости судна
8 Оценка остойчивости по правилам российского морского регистра судоходства
10 Проектирование набора корпуса по правилам РС
10.3 Расчет элементов конструкции корпуса
11 Прочность судна. Расчет внешних сил, вызывающих общий изгиб
11.1 Внешние нагрузки, действующие на судно
11.2 Распределение масс судна по теоретическим отсекам
11.3 Расчет изгибающих моментов и перерезывающих сил на тихой воде и на волнении
11.4 Расчет эквивалентного бруса
10.5 Проверка прочности корпуса по правилам Регистра
12 Анализ специальных систем танкера
12.1 Специальные системы танкера
12.2 Грузовые, зачистные и балластные сиситемы
ИМО= 12,19 м).
Давление ветра рV принимается согласно части IV раздела 2 Правил РС [2].
Принимаем рV = 353 Па.
По полученным данным рассчитаем плечо кренящего момента от постоянно дующего ветра:
lw1=0,023 м
Точка пересечения плеча кренящего момента lw1 с диаграммой статической остойчивости определяет угол крена от постоянно дующего ветра – θw.
Следующее, что определяем это плечо кренящего момента от шквала – lw2:
lw2=1,5*lw1=0,034 м
Полученное значение lw1 и lw2 откладывается на диаграмме статической остойчивости рисунок 8.1
Амплитуда качки судна с круглой скулой вычисляется по формуле
θ1=109·k·X1·X2·
, (8.2)
где k – коэффициент, учитывающий влияние скуловых и\или брусковых килей (k=1,0)
X1 – безразмерный множитель, определяющийся в зависимости от отношения
(X1=1)
X2 – безразмерный множитель, определяющийся в зависимости от коэффициента общей полноты судна Cb (X2=1)
r – параметр, рассчитываемый по формуле
, (8.3)
r не должно превышать 1.
S – безразмерный множитель, определяющийся в зависимости от района плавания судна и периода качки T( S = 0,04).
где k –коэффициент, учитывающий влияние скуловых и/или брусковых килей (k= 1,0),
r – параметр (не должен превышать 1), рассчитываемый по формуле
S – безразмерный множитель S=0,04, определяющийся в зависимости от района плавания судна и периода качки T, которая рассчитывается по формуле:
где c рассчитывается по формуле:
Остойчивость судна оценивается по критерию погоды
.
Рисунок 8.1 – ДСО при 100% грузу и 100% запаса
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 0,386 м2;
b = 0,83 м2.
Таким образом, K = 2,15
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.2.
Таблица 8.2 – Характеристики остойчивости для случая 100% груза и 100% запасов
8.2 Оценка остойчивости для случая 0% груза и 10% запасов.
Плечо кренящего момента от постоянно дующего ветра принимается постоянным для всех углов крена и определяется по формуле (5.1).
Δ – водоизмещение судна для данного случая нагрузки, (Δ =11742).
Площадь парусности АV боковой поверхности части судна и палубного груза выше ватерлинии рассчитывается средствами AutoCAD (AV = 1668,78 м2).
Расстояние по вертикали от центра парусности ЦП до центра погруженной площади боковой поверхности также рассчитывается в AutoCAD (ZИМО= 10,78 м).
Давление ветра рV принимается согласно части IV раздела 2 Правил РС [2].
Принимаем рV = 353 Па.
По полученным данным рассчитаем плечо кренящего момента от постоянно дующего ветра:
lw1
=0,055м
Точка пересечения плеча кренящего момента lw1 с диаграммой статической остойчивости определяет угол крена от постоянно дующего ветра – θS. Следующее, что определяем это плечо кренящего момента от шквала – lw2:
lw2= lw1*2=0,083 м
Полученное значение lw1 и lw2 откладывается на диаграмме статической остойчивости рисунок 8.2.
где k –коэффициент, учитывающий влияние скуловых и/или брусковых килей (k= 1,0),
X1 – безразмерный множитель, определяющийся в зависимости от отношения B / d (X1 = 0,78),
X2 – безразмерный множитель, определяющийся в зависимости от коэффициента общей полноты судна CB (X2 = 1),
r – параметр (не должен превышать 1), рассчитываемый по формуле
S – безразмерный множитель S=0,04 , определяющийся в зависимости от района плавания судна и периода качки T, которая рассчитывается по формуле:
где c рассчитывается по формуле:
Остойчивость судна оценивается по критерию погоды
.
Рисунок 8.2 – ДСО при 0% грузу и 10% запаса
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 3,07 м2;
b = 13,3 м2.
Таким образом, K = 4,33. Критерии остойчивости приведены в таблице 8.3.
Таблица 8.3 – Характеристики остойчивости для случая 0% груза и 10% запасов
8.3 Оценка остойчивости для случая 100% груза и 10% запасов.
Δ =20347т
g = 9,81 м/с2
AutoCAD AV = 1119,04м2.
AutoCAD ZИМО= 11,97 м.
Принимаем рV = 353 Па.
lw1=0,024 м
lw2=1,5*lw1=0,036 м
X1 =1
X2=1
S=0,04
k=1,0
Остойчивость судна оценивается по критерию погоды .
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 5,1 м2;
b = 11,1 м2.
Таким образом, K = 2,18
Рисунок 8.3 – ДСО при 100% грузу и 10% запаса
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.3.
Таблица 8.3 – Характеристики остойчивости для случая 100% груза и 10% запасов
8.4 Оценка остойчивости для случая 0% груза и 100% запасов.
Δ =10895т
g = 9,81 м/с2
AutoCAD AV = 1753м2.
AutoCAD ZИМО= 10,12 м.
Принимаем рV = 353 Па.
lw1=0,059 м
lw2=1,5*lw1=0,088м
X1 =0,77
X2=1
S=0,07
k=1,0
Остойчивость судна оценивается по критерию погоды .
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 3,24 м2;
b = 17,3 м2.
Таким образом, K = 5,34
Рисунок 8.4 – ДСО при 0% грузу и 100% запаса
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.4.
Таблица 8.4 – Характеристики остойчивости для случая 0% груза и 100% запасов
Давление ветра рV принимается согласно части IV раздела 2 Правил РС [2].
Принимаем рV = 353 Па.
По полученным данным рассчитаем плечо кренящего момента от постоянно дующего ветра:
lw1=0,023 м
Точка пересечения плеча кренящего момента lw1 с диаграммой статической остойчивости определяет угол крена от постоянно дующего ветра – θw.
Следующее, что определяем это плечо кренящего момента от шквала – lw2:
lw2=1,5*lw1=0,034 м
Полученное значение lw1 и lw2 откладывается на диаграмме статической остойчивости рисунок 8.1
Амплитуда качки судна с круглой скулой вычисляется по формуле
θ1=109·k·X1·X2·
, (8.2)где k – коэффициент, учитывающий влияние скуловых и\или брусковых килей (k=1,0)
X1 – безразмерный множитель, определяющийся в зависимости от отношения
(X1=1)X2 – безразмерный множитель, определяющийся в зависимости от коэффициента общей полноты судна Cb (X2=1)
r – параметр, рассчитываемый по формуле
, (8.3)r не должно превышать 1.
S – безразмерный множитель, определяющийся в зависимости от района плавания судна и периода качки T( S = 0,04).
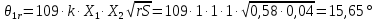
где k –коэффициент, учитывающий влияние скуловых и/или брусковых килей (k= 1,0),
r – параметр (не должен превышать 1), рассчитываемый по формуле
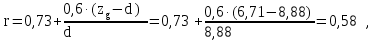
S – безразмерный множитель S=0,04, определяющийся в зависимости от района плавания судна и периода качки T, которая рассчитывается по формуле:
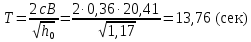
где c рассчитывается по формуле:
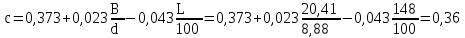
Остойчивость судна оценивается по критерию погоды
.
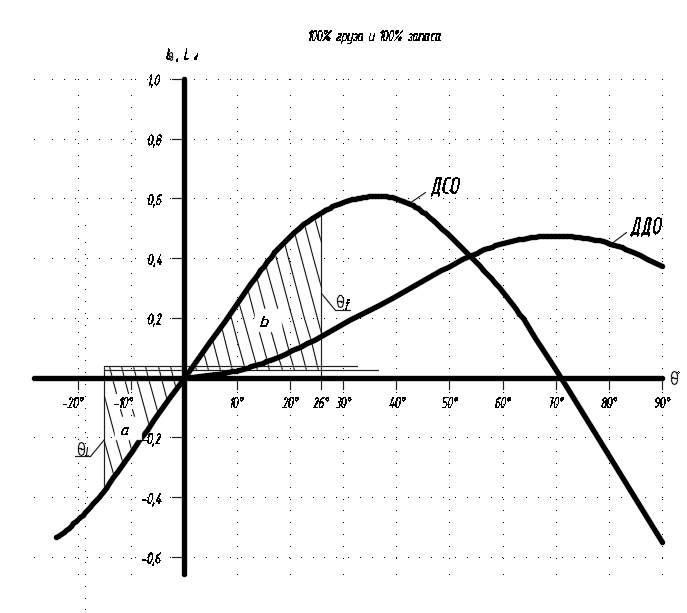
Рисунок 8.1 – ДСО при 100% грузу и 100% запаса
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 0,386 м2;
b = 0,83 м2.
Таким образом, K = 2,15
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.2.
Таблица 8.2 – Характеристики остойчивости для случая 100% груза и 100% запасов
| Наименование критерия | Требование норм | Фактическое значение |
| Критерий погоды | ≥1.0 | 2,15 |
| Максимальное плечо диаграммы статической остойчивости, м | ≥0.25 | 0,6 |
| Угол максимума диаграммы статической остойчивости | ≥30° | 40° |
| Угол заката диаграммы статической остойчивости | ≥60° | 71° |
| Начальная метацентрическая высота, м | ≥0.15 | 1,17 |
8.2 Оценка остойчивости для случая 0% груза и 10% запасов.
Плечо кренящего момента от постоянно дующего ветра принимается постоянным для всех углов крена и определяется по формуле (5.1).
Δ – водоизмещение судна для данного случая нагрузки, (Δ =11742).
Площадь парусности АV боковой поверхности части судна и палубного груза выше ватерлинии рассчитывается средствами AutoCAD (AV = 1668,78 м2).
Расстояние по вертикали от центра парусности ЦП до центра погруженной площади боковой поверхности также рассчитывается в AutoCAD (ZИМО= 10,78 м).
Давление ветра рV принимается согласно части IV раздела 2 Правил РС [2].
Принимаем рV = 353 Па.
По полученным данным рассчитаем плечо кренящего момента от постоянно дующего ветра:
lw1
=0,055м
Точка пересечения плеча кренящего момента lw1 с диаграммой статической остойчивости определяет угол крена от постоянно дующего ветра – θS. Следующее, что определяем это плечо кренящего момента от шквала – lw2:
lw2= lw1*2=0,083 м
Полученное значение lw1 и lw2 откладывается на диаграмме статической остойчивости рисунок 8.2.
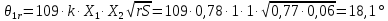
где k –коэффициент, учитывающий влияние скуловых и/или брусковых килей (k= 1,0),
X1 – безразмерный множитель, определяющийся в зависимости от отношения B / d (X1 = 0,78),
X2 – безразмерный множитель, определяющийся в зависимости от коэффициента общей полноты судна CB (X2 = 1),
r – параметр (не должен превышать 1), рассчитываемый по формуле
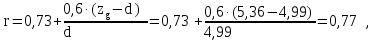
S – безразмерный множитель S=0,04 , определяющийся в зависимости от района плавания судна и периода качки T, которая рассчитывается по формуле:
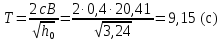где c рассчитывается по формуле: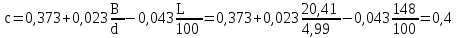 Остойчивость судна оценивается по критерию погоды
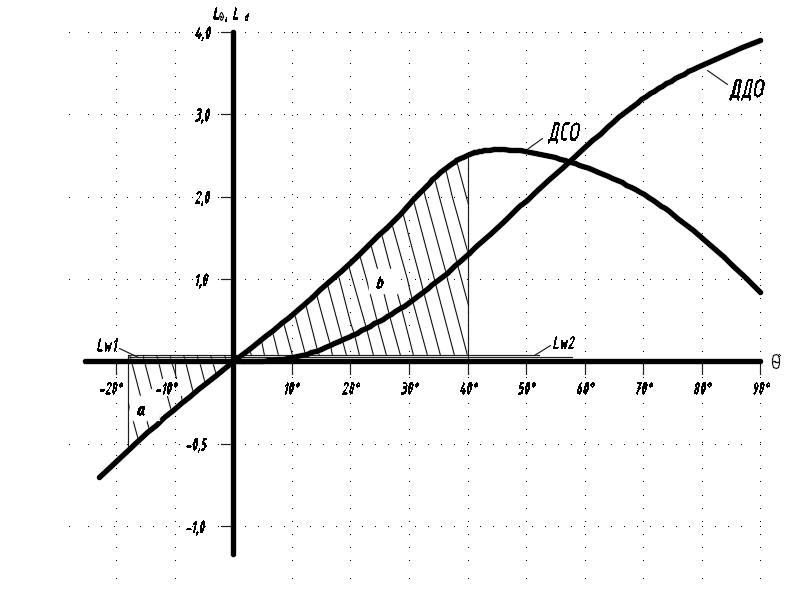
. Рисунок 8.2 – ДСО при 0% грузу и 10% запаса
По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 3,07 м2;
b = 13,3 м2.
Таким образом, K = 4,33. Критерии остойчивости приведены в таблице 8.3.
Таблица 8.3 – Характеристики остойчивости для случая 0% груза и 10% запасов
| Наименование критерия | Требование норм | Фактическое значение |
| Критерий погоды | ≥1.0 | 4,33 |
| Максимальное плечо диаграммы статической остойчивости, м | ≥0.25 | 2,54 |
| Угол максимума диаграммы статической остойчивости | ≥30° | 50° |
| Угол заката диаграммы статической остойчивости | ≥60° | >90° |
| Начальная метацентрическая высота, м | ≥0.15 | 3,24 |
8.3 Оценка остойчивости для случая 100% груза и 10% запасов.
Δ =20347т
g = 9,81 м/с2
AutoCAD AV = 1119,04м2.
AutoCAD ZИМО= 11,97 м.
Принимаем рV = 353 Па.
lw1=0,024 м
lw2=1,5*lw1=0,036 м
X1 =1
X2=1
S=0,04
k=1,0
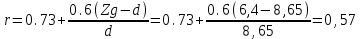
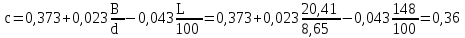
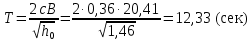
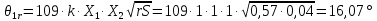
Остойчивость судна оценивается по критерию погоды
.По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 5,1 м2;
b = 11,1 м2.
Таким образом, K = 2,18
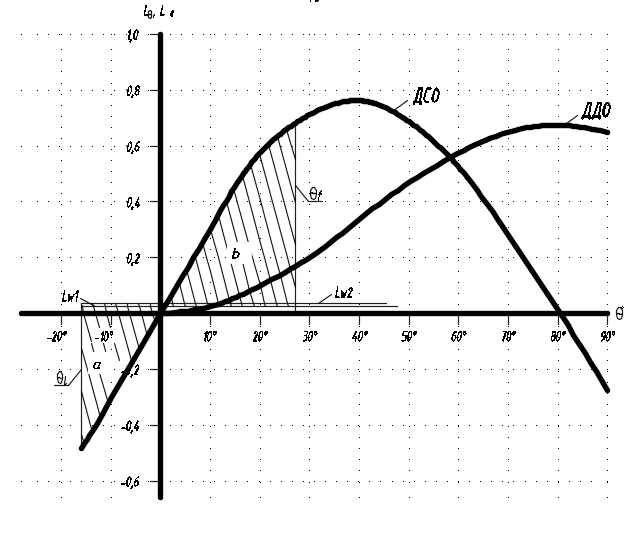
Рисунок 8.3 – ДСО при 100% грузу и 10% запаса
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.3.
Таблица 8.3 – Характеристики остойчивости для случая 100% груза и 10% запасов
| Наименование критерия | Требование норм | Фактическое значение |
| Критерий погоды | ≥1.0 | 2,18 |
| Максимальное плечо диаграммы статической остойчивости, м | ≥0.25 | 0,76 |
| Угол максимума диаграммы статической остойчивости | ≥30° | 40° |
| Угол заката диаграммы статической остойчивости | ≥60° | 80° |
| Начальная метацентрическая высота, м | ≥0.15 | 1,46 |
8.4 Оценка остойчивости для случая 0% груза и 100% запасов.
Δ =10895т
g = 9,81 м/с2
AutoCAD AV = 1753м2.
AutoCAD ZИМО= 10,12 м.
Принимаем рV = 353 Па.
lw1=0,059 м
lw2=1,5*lw1=0,088м
X1 =0,77
X2=1
S=0,07
k=1,0
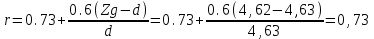
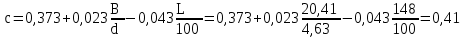
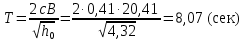
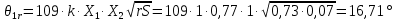
Остойчивость судна оценивается по критерию погоды
.По измерениям на диаграмме статической остойчивости судна с помощью AutoCAD имеем:
a = 3,24 м2;
b = 17,3 м2.
Таким образом, K = 5,34
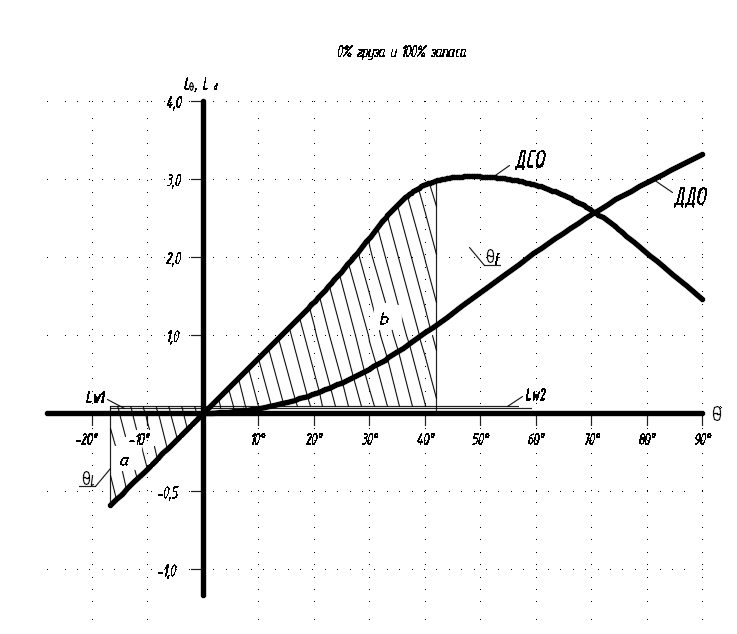
Рисунок 8.4 – ДСО при 0% грузу и 100% запаса
Кроме выполнения условий по критерию погоды Правила Регистра предъявляют требования к диаграмме статической остойчивости и начальной метацентрической высоте. Критерии остойчивости приведены в таблице 8.4.
Таблица 8.4 – Характеристики остойчивости для случая 0% груза и 100% запасов
| Наименование критерия | Требование норм | Фактическое значение |
| Критерий погоды | ≥1.0 | 5,34 |
| Максимальное плечо диаграммы статической остойчивости, м | ≥0.25 | 3,06 |
| Угол максимума диаграммы статической остойчивости | ≥30° | 50° |
| Угол заката диаграммы статической остойчивости | ≥60° | >90° |
| Начальная метацентрическая высота, м | ≥0.15 | 4,32 |