Файл: Контрольная работа по дисциплине статистический анализ и планирование эксперимента Вариант 42.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 238
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
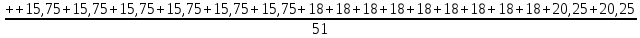 +
++
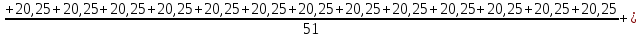
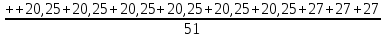 = 18,26
= 18,26Средневзвешенное интервального ряда.
Для заданных исходных данных получим:
X =
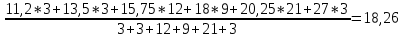
Мода интервального ряда.
Мода для интервального ряда и для заданного ряда случайной величины имеет одно значение с частотой 21
M = 20,25
Медиана интервального ряда.
Медиана для интервального ряда имеет значение:
Me = (18+18)/2 = 18.
Дисперсия интервального ряда.
Расчетные значения дисперсии для интервального ряда приведены в таблице 1.9.
Таблица 1.9 – Расчет дисперсии ряда
| Номер интервала | Среднее значение xt | Частоты ni | Среднее арифметическое | (xi-xср.ар)2*nt | 1/(n-1) |
| 1 | 11,25 | 3 | 18,26 | 147,42 | 1/50 |
| 2 | 13,5 | 3 | 67,97 | ||
| 3 | 15,75 | 12 | 75,60 | ||
| 4 | 18 | 9 | 0,61 | ||
| 5 | 20,25 | 21 | 83,16 | ||
| 6 | 22,5 | 0 | 0,00 | ||
| 7 | 24,75 | 0 | 0,00 | ||
| 8 | 27 | 3 | 229,16 |
Тогда дисперсия для интервального ряда примет значение:
D = 12,07
Среднее квадратическое отклонение интервального ряда
Для заданных исходных данных получим:
σ =
 =
= 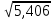 =3,47.
=3,47.Коэффициент вариации интервального ряда
Для заданных исходных данных получим:
δ =
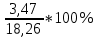
= 0,19 %
Характеристики описательной статистики интервального ряда.
Средствами программы Excel рассчитаны характеристики описательной статистики заданного ряда. Для корректного расчета данных характеристик построим полный интервальный ряд для средних значений случайной величины в табл. 1.10.
Таблица 1. 10- Полный интервальный ряд
| 11,25 | 13,5 | 15,75 | 15,75 | 18 | 18 | 20,25 | 20,25 | 20,25 | 20,25 | 27 |
| 11,25 | 15,75 | 15,75 | 15,75 | 18 | 18 | 20,25 | 20,25 | 20,25 | 20,25 | |
| 11,25 | 15,75 | 15,75 | 15,75 | 18 | 20,25 | 20,25 | 20,25 | 20,25 | 20,25 | |
| 13,5 | 15,75 | 15,75 | 18 | 18 | 20,25 | 20,25 | 20,25 | 20,25 | 27 | |
| 13,5 | 15,75 | 15,75 | 18 | 18 | 20,25 | 20,25 | 20,25 | 20,25 | 27 | |
Числовые значения, рассчитанные в программе Excel, приведены на рисунке 1.11.
| Среднее | 18,26470588 |
| Стандартная ошибка | 0,486655844 |
| Медиана | 18 |
| Мода | 20,25 |
| Стандартное отклонение | 3,475417876 |
| Дисперсия выборки | 12,07852941 |
| Эксцесс | 0,997659533 |
| Асимметричность | 0,303961766 |
| Интервал | 15,75 |
| Минимум | 11,25 |
| Максимум | 27 |
| Сумма | 931,5 |
| Счет | 51 |
Рисунок 1.11 – Характеристики описательной статистики
Вывод. Сравнив расчеты, полученные вручную и расчеты на ПК, я пришел к выводу, что они выполнены корректно.
2.1 Статистический анализ двумерной последовательности случайных величин
Цель работы. Освоить компетенции выполнения статистического анализа двумерных данных, выявить зависимость (связь) между случайными величинами.
2.1.1 Исходные данные
В качестве исходных данных принято двух последовательных случайных величин:
первая – агрегаты в работе, %
вторая – коэффициент использования.
Исходные данные представлены в таблице 2.1.
Таблица 2.1 – Исходные данные
|
|
Примем:
в качестве аргумента Xi - карбонатность;
в качестве функции Yi – песчанистость.
Взаимосвязь между двумя случайными величинами может быть оценена следующими методами:
-
Визуальный метод -
Корреляционный анализ -
Регрессионный анализ
-
Визуальный анализ
Визуальный метод –это анализ в основе которого лежит зрительное восприятие человеком данных, изображенных в виде графиков, диаграмм или гистограмм и т.д., позволяющее дать предварительную оценку этим данным, до проведения вычислений.
По данным таблицы 2.1 построен точечный график (рис. 2.1).
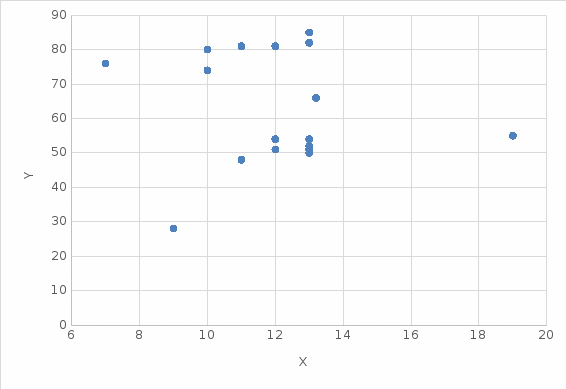
Рисунок 2.1 – Точечный график
Вывод: визуально определена разрозненность точек, что предварительно означает, что зависимость слаба.
-
Корреляционный анализ
Корреляционная зависимость – статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми).
Корреляционный анализ выполнен с помощью пакета «Анализ данных» программы Excel, результаты которого показаны в таблице 2.2.
Таблица 2.1 - Результаты корреляционного анализа
| | Ккар%, X | Кпес. %, Y |
| Ккар%, X | 1 | -0,149780993 |
| Кпес. %, Y | -0,149780993 | 1 |
Вывод: Предварительные выводы из визуального анализа подтвердились, связь отрицательная слабая (таблица Чеддока).
-
Регрессионный анализ
Регрессионный анализ – определяет форму (вид) связи между этими переменными. Регрессионный анализ используется для прогнозирования одной переменной на основании другой (как правило, Y на основании X), или показывает, как можно управлять одной переменной с помощью другой.