Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 174
Скачиваний: 3
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
| | AD- общий перпендикуляр между АВи СD | 1 | |
| Ответ:7 | 1 | | |
| 6 | Выполнен рисунок 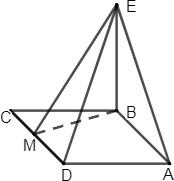 | 1 | |
| Обосновано, что линейный угол между плоскостями равен углу EMB, где M– основание высоты ромба, опущенной из Bна сторону AD | 1 | | |
| Высота ромба равна m3 , тогда искомый угол 2 равен 45° | 1 | | |
| Итого: | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 8 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания за 3 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания * | Тип задания * | Время на выполнение, мин* | Балл* | Балл за раздел |
| Перпендикул ярность в пространстве | 10.1.2 Знать определение и свойства прямоугольного параллелепипеда | Знание и понимание | 1 | 1 | РО | 4 | 2 | 4 |
| 10.3.6 Знать формулу площади ортогональной проекции плоской фигуры на плоскость и применять ее при решении задач | Применение | 1 | 6 | РО | 4 | 2 | ||
| Прямоугольн ая система координат и векторы в пространстве | 10.4.2 Выполнять сложение векторов и умножение вектора на число | Применение | 1 | 2 | КО | 6 | 2 | 16 |
| 10.4.3 Знать определения коллинеарных и компланарных векторов в пространстве | Знание и понимание | 1 | 3 | КО | 6 | 2 | ||
| 10.4.15 Раскладывать вектор по трем некомпланарным векторам | Применение | 2 | 4,7 | РО | 8 | 4 | ||
| 10.4.7 Уметь находить расстояние между двумя точками в пространстве | Применение | 2 | 5,8 | РО | 12 | 8 | ||
| ИТОГО: | | | 8 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 3 четверть
-
Дан прямоугольный параллелепипед
ABCDA1B1C1D1 , где
B1D 5, B1C1
5 3
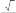2 .Найдите угол между
B1Dи гранью
DD1C1C.
[2]
-
ABCDA1B1C1D1 ‒ параллелепипед.-
Укажите вектор, равный сумме векторов
-
AB B1C1 DD1 CD.
[1]-
Пусть
A1Cпересекает
B1Dв точке M,
B1D x DM. Найдите x.
[1]-
Дан параллелепипед
ABCDA1B1C1D1 .
а) Точки Eи F‒ середины ребер
B1C1
и C1D1
соответственно. Запишите векторы с
началом и концом в вершинах параллелепипеда, которые сонаправлены с EF.
[1]
b) Объясните, какие из следующих трех векторов: компланарны.AA1 ,CC1 , BB1 или
AB, AD, AA1
[1]-
ABCDA1B1C1D1
-
параллелепипед. Точка K– середина ребра CC1. Разложите вектор AK
по векторам
AB, AD, AA1 .
[2]
-
Дан равнобедренный треугольник ABC (AC=CB), где A(1; ‒2; 1), B(3; 2; ‒3).Точка C
лежит на оси ординат. Найдите стороны треугольника ABC.
-
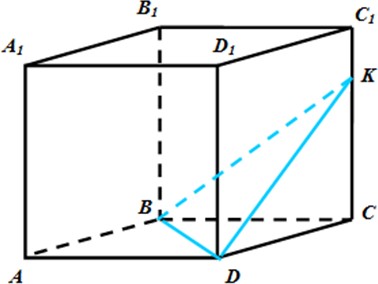
Ребро куба
ABCDA1B1C1D1
[4]
равно 2 см. Через диагональ основания BDпод углом 45° к
плоскости основания проведена плоскость BDK, пересекающая боковое ребро в точке K. Найдите площадь треугольника BDK.
[2]
-
Дан тетраэдр DABC. Точка K – середина ребра AC, а точка M – середина отрезка KD.
DA a, DB b, DC c. Разложите BMпо векторам a, b, c.[2]
-
В треугольнике MFPвершины имеют следующие координаты: M(0; 0; 0), F(2; ‒1; 3),