Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 162
Скачиваний: 3
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
P(‒1; 1; 1). Найдите диаметр окружности, описанной вокруг этого треугольника.
[4]
| № | Ответ | Балл | Дополнительная информация |
| 1 | Обосновано, что искомый угол B1DC1 | 1 | |
| B1DC1 = 60° | 1 | ||
| 2 | AB B1C1 DD1 CD AB BC CD DD1 AD1 | 1 | |
| x= ‒2 | | ||
| 3 | BD, B1D1 | 1 | |
| AA1 ,CC1 , BB1 (они равны, т. е. параллельны одной плоскости) | 1 | ||
| 4 | AK AB BC CKилиэквивалент | 1 | |
| AB AD 1 AA 2 1 | 1 | ||
| 5 | AC BC 0 12 y 22 0 12 0 32 y 22 0 32 или эквивалент | 1 | |
| y=2 | 1 | ||
| AC= CB= 3 2 | 1 | ||
| AB= 6 | 1 | ||
| 6 | Указано, что ΔBDC– проекция ΔBDKна плоскость основания и S(BDC)=2 | 1 | |
| S BDK S BDC S BDK 2 2 cos45 | 1 | ||
| 7 | BM BD DM | 1 | |
| BD 1 DA DC 1 a b 1 c 4 4 4 | 1 |
| 8 | MF2 4 1 9 14,MP2 111 3,FP2 9 4 4 17 | 2 | 1 балл за одну верно вычисленную сторону 1 балл за все верно вычисленные стороны |
| MF2 MP2 FP2 ∆MFP-прямоугольный | 1 | | |
| Диаметр 17 | 1 | | |
| Итого: | 20 | | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания за 4 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задани я* | Тип задания* | Время на выполнени е, мин* | Балл* | Балл за раздел |
| Прямоугольн ая система координат и векторы в пространстве | 10.4.4 Знать определение и свойства скалярного произведения векторов в пространстве | Знание и понимание | 2 | 1,6 | КО/РО | 8 | 3 | 20 |
| 10.4.17 Вычислять угол между двумя векторами в пространстве | Применение | 2 | 2, 7 | РО | 14 | 8 | ||
| 10.4.18 Знать и применять условие перпендикулярности векторов в пространстве | Применение | 1 | 4 | КО/РО | 6 | 3 | ||
| 10.4.10 Знать уравнение сферы и применять его при решении задач | Применение | 1 | 3 | КО/РО | 6 | 3 | ||
| 10.4.21 Уметь переходить от канонического вида к параметрическому виду уравнения прямой | Применение | 1 | 5 | КО | 6 | 3 | ||
| ИТОГО: | | | 7 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 4 четверть
1. Скалярный квадрат вектора равен 20. Найдите модуль этого вектора.
[1]
2. Точки А(14;8;1); B(7;3;1);С(6;4;1); D(1;7;1) являются вершинами ромба ABCD.
Найдите острый угол ромба.
[5]
3.
а) Напишите уравнение сферы с центром в начале координат, если плоскость x= 2 касается этой сферы.
b) Сфера задана уравнением ее радиус.
[1]
x2 4x y2 z2 0 . Найдите координаты центра сферы и
[2]
4.
[1]
Покажите, что aи cперпендикулярны для всех ненулевых значений pи q.
[2]
5.
а) Прямая задана уравнением
x 2
y z 6 . Задайте прямую параметрически.
5 7 11
[1]
-
Дан прямой m.
2
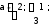 5
5 -
направляющий вектор прямой m,
M7;1;0
принадлежит
-
Напишите каноническое уравнение прямой m.
[1]
-
Напишите параметрическое уравнение прямой m.
-


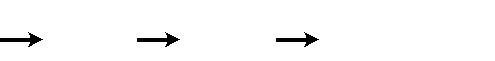 Дано: c b a 0 , c ab 0 . Докажите, что b a c 0 .
Дано: c b a 0 , c ab 0 . Докажите, что b a c 0 .
[1]
[2]
-
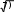 Найдите угол между вектором u→(3;4;
Найдите угол между вектором u→(3;4;
и осью ОY.
[3]
