Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 169
Скачиваний: 3
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания за 2 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задани я* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Перпендикул ярность в пространстве | 10.2.8 Знать определение перпендикуляра, наклонной и проекции наклонной в пространстве | Знание и понимание | 1 | 1 | КО | 6 | 2 | 20 |
| 10.2.9 Знать определение угла между двумя прямыми в пространстве | Знание и понимание | 1 | 2 | КО | 7 | 4 | ||
| 10.3.1 Знать теорему о трех перпендикулярах и применять её при решении задач | Применение | 1 | 3 | РО | 9 | 6 | ||
| 10.3.5 Уметь находить расстояние от точки до плоскости и между скрещивающимися прямыми | Применение | 2 | 4,5 | РО | 9 | 5 | ||
| 10.3.3 Знать определение угла между плоскостями (двугранный угол), уметь изображать и находить его величину | Применение | 1 | 6 | РО | 9 | 3 | ||
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 2 четверть
1.
-
ABCD – параллелограмм, BE и DF – перпендикуляры к плоскости ABC. Докажите, что плоскости ABEи DFCпараллельны.
[1]
-
Из точки, не лежащей в плоскости, проведено множество равных наклонных к этой плоскости. Какую фигуру образуют основания наклонных?
-
В кубе
ABCDA1B1C1D1
точки Kи F– середины ребер
A1B1 и
B1C1 соответственно.
[1]
Mи P– точки пересечения диагоналей граней
A1D1DAи
DCC1D1 соответственно.
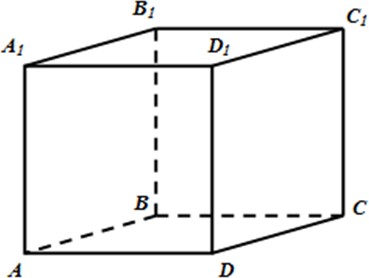
Заполните таблицу, указав градусные меры углов между данными прямыми.
| Прямые | Градусная величина угла между ними |
| KFи MP | |
| KFи BD | |
| DC1 и KF | |
| KMи FP | |
[4]
-
Отрезок АDперпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ=АС=5 см, ВС=6 см, АD=12 см.-
Выполните чертеж по условию задачи.
-
[1]
-
Найдите расстояния от концов отрезка АDдо прямой ВС.
[5]
-
Отрезок ABрасположен вне плоскости αпо одну сторону от нее. Расстояние от точек Aи B
до плоскости равны 10 и 14. Найдите расстояние от середины отрезка ABдо плоскости α.
[2]
-
К плоскости квадрата ABCDпроведен перпендикуляр KD. Сторона квадрата равна 7 см. Найдите расстояние между прямыми АВи KD.
-
ABCD– ромб, в котором
[3]
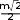 A 60, AB m, BE ABC , BE . Выполните
A 60, AB m, BE ABC , BE . Выполнитерисунок и найдите угол между плоскостями AEDи ABC.
[3]
 Схема выставления баллов
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация | |
| | Т.к АВCD- параллелограмм, то AB// CD; т.к | | | |
| 1 | EB ( ABC) и FD (ABC) , то EB// FD (AEB) //( FCD) | 1 | Применен признак параллельности плоскостей | |
| | Окружность | 1 | | |
| 2 | KFи MP | 0° | 1 | |
| KFи BD | 90° | 1 | ||
| DC1 и KF | 60° | 1 | ||
| KMи FP | 0° | 1 | ||
| 3 | 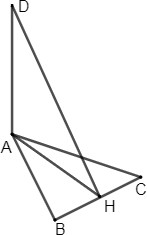 | 1 | Выполнен чертеж | |
| Расстояние от точки А до прямой ВС есть длина перпендикуляра АН; AH BC AH- высота и медиана треугольника АВС | 1 | Применяет свойства равнобедренного треугольника | ||
| DH BС | 1 | Применена теорема о трех перпендикулярах | ||
| AH2 AС2 HC2 25 9 16 | 1 | | ||
| DH2 DA2 HA2 144 16 160 | 1 | | ||
| DH 4 10 | 1 | | ||
| | ABCD – трапеция, где C и D- основания | | Дает обоснование | |
| | перпендикуляров, опущенных из A и B | 1 | | |
| 4 | соответственно на плоскость | | | |
| | Искомое расстояние – средняя линия трапеции и равно 12 | 1 | | |
| 5 | АВи СD-скрещивающиеся прямые | 1 | | |