Файл: Спецификация суммативного оценивания за четверть по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 168
Скачиваний: 3
СОДЕРЖАНИЕ
Уровни мыслительных навыков по предмету «Геометрия»
Правила проведения суммативного оценивания
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 1 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 2 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 3 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Структура суммативного оценивания
Характеристика заданий суммативного оценивания за 4 четверть
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 1 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания за 1 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задани я* | Время на выполнение, мин* | Балл* | Балл за раздел |
| | 10.2.1 Знать аксиомы стереометрии, их следствия; иллюстрировать и записывать их с помощью математических символов | Знание и понимание | 1 | 1а,b | КО | 6 | 3 | |
| | 10.2.2 Знать определение параллельных и | | | | | | | |
| | скрещивающихся прямых в пространстве, определять и изображать | Знание и понимание | 1 | 2 | КО | 6 | 4 | |
| | их | | | | | | | |
| Аксиомы стереометрии. Параллельнос ть в пространстве | 10.2.3 Знать свойства параллельных прямых в пространстве и применять их при решении задач | Применение | 1 | 3 | РО | 7 | 3 | 20 |
| 10.1.1 Знать определение тетраэдра и параллелепипеда, уметь изображать тетраэдр, параллелепипед и их элементы | Знание и понимание | 1 | 5 | КО | 8 | 2 | ||
| | на плоскости | | | | | | | |
| | 10.2.4 Знать признак и свойства | | | | | | | |
| | параллельности прямой и плоскости, | Применение | 1 | 4 | КО | 7 | 3 | |
| | применять их при решении задач | | | | | | | |
| | 10.2.5 Знать признак и свойства | | | | | | | |
| | параллельности плоскостей, применять | Применение | 1 | 6 | КО | 6 | 5 | |
| | их при решении задач | | | | | | | |
| ИТОГО: | | | 6 | | | 40 | 20 | 20 |
| Примечание:*-разделы,вкоторыеможновноситьизменения | ||||||||
Образец заданий и схема выставления баллов Задания суммативного оценивания за 1 четверть
1.
а) Три точки в пространстве не определяют положение плоскости, которая проходит через них. Как расположены эти точки?
[1]
b) Прямые aи bпараллельны. Прямая aпересекает плоскость αв точке A, а прямая
bпересекает плоскость αв точке B. Точки E,Fb. Укажите взаимное расположение прямых EFи AB.
[2]
-
В кубе
ABCDA1B1C1D1 точки Kи F– середины ребер
A1B1
и B1C1 соответственно.
Mи P– точки пересечения диагоналей граней
A1D1DAи
DCC1D1
соответственно.
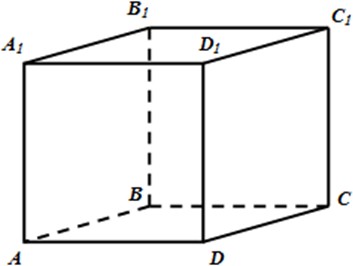
Заполните таблицу расположения прямых.
| Прямые | Расположение прямых |
| KFи MP | |
| KFи BD | |
| DC1 и KF | |
| KMи FP | |
[4]
-
Прямые aи bпересекаются в точке M. Плоскости αи βпараллельны.
Прямая aпересекает плоскость αв точке A, а плоскость βв точке B. Прямая bпересекает плоскость αв точке C, а плоскость β в точке D.
AM 2 .Найдите MC.
AB 3 CD
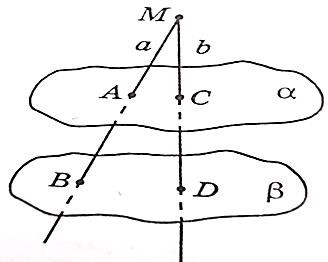
[3]
-
Отрезок АВ лежит в плоскости α. Точка М не принадлежит плоскости α. Точки К и Р – середины отрезков МАи МВсоответственно. Докажите, что прямая КРпараллельна плоскости α.Выполните рисунок по условию задачи.
-
Постройте наклонный параллелепипед
ABCDA1B1C1D1 .
[3]
Найдите центры граней
ABB1 A1
и CDD1C1 и проведите через найденные точки прямую.
[2]
-
Параллельные плоскости α и β пересекают сторону ???????? угла ???????????? соответственно в точках P и H, а сторону АС этого угла – соответственно в точках Q и К. Найдите АНи АК, если РН=2РА, РН=12 см, АQ= 5 см. Выполните рисунок по условию задачи.
[5]
Схема выставления баллов
Схема выставления баллов
| № | Ответ | Балл | Дополнительная информация | |
| 1 | Эти точки лежат на одной прямой | 1 | | |
| Прямые пересекаются или параллельны | 2 | 1 балл за каждый случай расположения прямых | ||
| 2 | KFи MP | параллельны | 1 | |
| KFи BD | скрещиваются | 1 | ||
| DC1 и KF | скрещиваются | 1 | ||
| KMи FP | параллельны | 1 | ||
| 3 | AC || BD | 1 | | |
| Δ AMCΔ BMD | 1 | |||
| MC 2 CD 3 | 1 | |||
| 4 | 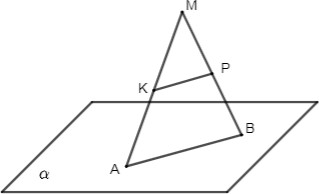 | 1 | Выполнен чертеж | |
| КР- средняя линия треугольника КР || АВ, тк. АВ лежит в плоскости | 1 | Применяет теорему о средней линии треугольника | ||
| | 1 | Применяет признак параллельности прямой и плоскости, | ||
| 5 | 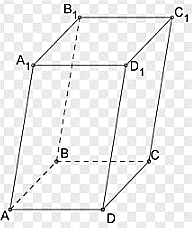 | 1 | Построен наклонный параллелепипед | |
| Проведена прямая через точки пересечения диагоналей граней ABB1A1 и CDD1C1 | 1 | | ||
| 6 | 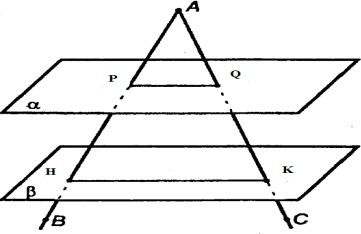 | 1 | По условию задачи изображен рисунок | |
| ???? ???????????? ???? ???????????? | 1 | Даёт обоснование | ||
| РА= 6 см | 1 | | ||
| АН= АР+ РН, АН = 18 см | 1 | | ||
| AK=15 см | 1 | | ||
| Итого: | 20 | | ||