Файл: Тарасевич Л.С., Гребенников П.И., Леусский А.И. - Микроэкономика, 4-е изд., 2006.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.09.2024
Просмотров: 632
Скачиваний: 0
СОДЕРЖАНИЕ
Глава 3. Теория потребительского спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
Глава 5. Ценообразование на монополизированном рынке
Глава 9. Отказы рынка и аллокативная роль государства
Глава 10. Микроэкономика внешней торговли
Глава 1. Введение в микроэкономику
1.1. Микроэкономика как часть современной экономической теории
1.2. Методы экономического анализа
1.3. Логическая структура курса
Глава 2. Теория производства и предложения благ
2.1. Производственная функция и техническая результативность производства
2.2. Затраты производства и функция затрат
2.3. Прибыль и условия ее максимизации
2.4. Функция предложения и излишек производителя
Глава 3. Теория потребительского спроса
3.3. Эффект замены и эффект дохода
3.4. Компенсационное и эквивалентное изменения дохода и излишки потребителя 7
3.5. Выявление предпочтений потребителя
3.6. Рыночный спрос и эластичность спроса
Часть II. Цена отраслевого равновесия
Глава 4. Ценообразование на рынке совершенной конкуренции
4.1. Отраслевое равновесие и его разновидности
4.2. «Паутинообразная» модель ценообразования
4.3. Величина равновесной цены
4.4. Особенности рынка совершенной конкуренции
4.5. Последствия государственного регулирования цен
Глава 5. Ценообразование на монополизированном рынке
5.1. Цена, максимизирующая прибыль
5.3. Цены, максимизирующие выручку и норму прибыли
5.4. Отсутствие функции предложения
5.5. Последствия государственного регулирования
Глава 6. Ценообразование на рынках несовершенной конкуренции
6.1. Монополистическая конкуренция
6.2.1. Олигополия на рынке гомогенного блага
6.2.2. Олигополия на рынке гетерогенного блага
6.3. Олигополия в свете теории игр
Глава 7. Ценообразование факторов производства
7.1. Предложение факторов производства
7.2. Спрос на факторы производства
7.3. Прокатная цена фактора производства
7.4. Функциональное распределение результатов производства
7.5. Капитальная цена фактора производства
Глава 8. Общее экономическое равновесие и общественное благосостояние
8.1. Цены частичного и общего равновесия
8.2. Модель общего экономического равновесия Вальраса
8.3. Конкурентное равновесие и общественное благосостояние
8.4. Первая теорема общественного благосостояния
8.5. Вторая теорема общественного благосостояния
Глава 9. Отказы рынка и аллокативная роль государства
9.2. Интернализация внешних эффектов
9.3. Производство общественных благ
9.4. Асимметричность информации
Глава 10. Микроэкономика внешней торговли
10.1. Основы международного разделения труда
10.1.1. Исходная модель Рикардо
Доказательство первой теоремы общественного благосостояния
Докажем, что в условиях совершенной конкуренции всегда выполняется равенство (8.13).
Если хозяйство ведется в условиях совершенной конкуренции, то в состоянии равновесия в длинном периоде цены благ равны предельным затратам производства (см. равенство (4.3)). Следовательно, для любых двух благ i, j выполняется равенство
|
|
|
|
|
Отношение предельных затрат двух благ показывает, на сколько надо сократить производство одного блага, чтобы увеличить производство другого на единицу, т.е. MCi/MCj = MRPTi,j. Следовательно, в состоянии конкурентного равновесия
|
|
MRPTi,j = Pi/Pj |
. |
(8.14) |
Как было установлено в 3.2, потребители получают максимум полезности при использовании своего дохода, если набор покупаемых благ обеспечивает равенство. Поскольку на конкурентном рынке все потребители покупают блага по одним и тем же ценам, то
|
|
|
. |
(8.15) |
Из условий (8.14) и (8.15) следует, что в экономике с совершенной конкуренцией сформируются такие пропорции производства и потребления благ, при которых выполняется условие (8.13). Первая теорема общественного благосостояния доказана.
Из нее следует, что существует социальный механизм - рынок совершенной конкуренции, который обеспечивает Парето-эффективное состояние экономики в условиях, когда каждый индивид заботится лишь о своем благополучии. Для принятия хозяйственных решений, совокупность которых приводит к такому состоянию, суверенным экономическим субъектам требуется минимум информации - характеристики полезности благ и вектор равновесных цен. Полезность благ потребители определяют на основе собственного опыта или рекламы. Вектор равновесных цен устанавливается в результате конкурентного взаимодействия индивидов.
Теорема общественного благосостояния подтверждает знаменитый вывод А. Смита о том, что в рыночной экономике индивид, преследуя свои собственные интересы, часто более действенным способом служит интересам общества, чем тогда, когда сознательно стремится делать это, если под интересами общества А. Смит подразумевал достижение Парето-эффективного распределения ресурсов.
8.5. Вторая теорема общественного благосостояния
Проведенный в 8.4 анализ показал, что конкурентное равновесие есть Парето-эффективное состояние экономики. При заданных производственных ресурсах и предпочтениях потребителей возможно множество таких состояний и рынок совершенной конкуренции реализует одно из них. Парето-эффективные состояния экономики различаются степенью дифференциации индивидуальных благосостояний. В связи с этим возникает вопрос: для любого ли Парето-эффективного состояния существует вектор цен, приводящий экономику, функционирующую в условиях совершенной конкуренции, к этому состоянию?
Сформулируем
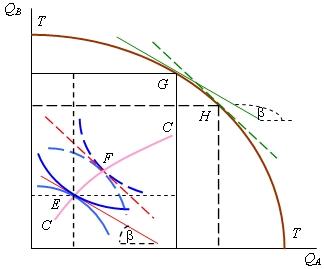
еще раз этот вопрос, используя рис. 8.11.
В заданных условиях на рынке установились
цены, представленные tg![]() ,
при которых ассортимент производимых
благ представляет точкаН,
а распределение их между потребителями
- точка F.
Можно ли найти такой вектор цен, при
котором распределение благ между
потребителями представляла бы, например,
точка Е?
,
при которых ассортимент производимых
благ представляет точкаН,
а распределение их между потребителями
- точка F.
Можно ли найти такой вектор цен, при
котором распределение благ между
потребителями представляла бы, например,
точка Е?
Ответ на этот вопрос дает вторая теорема общественного благосостояния, которая гласит: если технологии производства благ и предпочтения потребителей «выпуклы», то любому Парето-эффективному состоянию экономики можно подобрать систему цен, обеспечивающую общее равновесие в этом состоянии.
Выпуклость технологий означает убывание предельной нормы технического замещения факторов производства по мере увеличения использования одного из них (изокванты выпуклы к началу координат). Соответственно выпуклость индивидуальных предпочтений проявляется в убывании предельной нормы замещения двух благ по мере увеличения потребления одного из них (кривые безразличия выпуклы к началу координат).
|
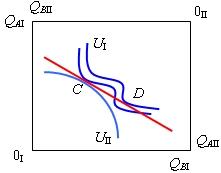
При выпуклости технологий и предпочтений потребителей изменение соотношений цен благ переводит экономику из одного оптимального состояния, представленного точками Н и F, в другое, которому соответствуют точки G и Е (рис. 8.12). Когда предпочтения хотя бы некоторых потребителей таковы, что представляющие их кривые безразличия не являются монотонно выпуклыми (см. рис. 8.13), тогда не существует системы цен, балансирующей спрос и предложение на всех рынках при Парето-эффективном состоянии экономики. Так, при ценах, соответствующих наклону бюджетной линии CD, потребитель I достигает максимума полезности при покупке набора благ, представленного точкой D, а потребитель II выбирает набор, соответствующий точке С. При такой структуре спроса на рынке блага А существует дефицит, а на рынке блага В - избыток. Равновесие на обоих рынках достигается при распределении благ, представленного точкой С, но оно не является Парето-эффективным, так как при переходе в точку D повышается благосостояние потребителя I без снижения благосостояния потребителя II. |
|
Из второй теоремы общественного благосостояния следует, что при выпуклых технологиях и предпочтениях потребителей две важнейшие задачи общественного хозяйства - оптимальное использование ограниченных факторов производства (аллокативная задача) и распределение благосостояния между членами общества (дистрибутивная задача) - могут решаться по отдельности. Используя свои возможности в перераспределении общественного благосостояния между гражданами, государство поддерживает справедливую дифференциацию индивидуальных доходов (выбирает точку на контрактной кривой в коробке Эджуорта), а рынок совершенной конкуренции через механизм ценообразования обеспечивает Парето-эффективное использование имеющихся производственных ресурсов. Но вновь возникает вопрос о критерии общественного благосостояния: какое распределение общественного богатства общество признает справедливым? |
Можно считать, что общество признает распределение справедливым, если никто из его членов не предпочитает свою долю доле другого (если никто никому не завидует). Таковым является уравнительное распределение, поскольку в этом случае у каждого будет точно такая же потребительская корзина, как у другого.
Однако при различных индивидуальных предпочтениях уравнительное распределение не является Парето-эффективным, поэтому оно неустойчиво. Между индивидами начнется обмен, в результате которого произойдет улучшение по Парето и после обмена потребительские корзины индивидов будут различаться.
Но не только уравнительное распределение общество может признать справедливым. Чтобы выяснить, признают ли индивиды сложившееся распределение справедливым, нужно между ними обменять принадлежащие им корзины благ. Если после обмена хотя бы один из них сочтет, что его благосостояние понизилось, то исходное распределение они должны признать справедливым.
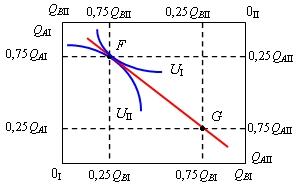
На рис. 8.14 исходное распределение двух благ между двумя потребителями представлено точкой F, т.е. потребительская корзина первого состоит из 0,75QA и 0,25QB, второго - из 0,25QA и 0,75QB. Если потребителям поменять их корзины, то возникнет распределение, отображаемое точкой G, которая лежит ниже обоих кривых безразличия, представляющих исходное благосостояние индивидов. Следовательно, распределение, соответствующее точке F, справедливо. В отличие от уравнительного распределения оно одновременно Парето-эффективно.
|
Признают ли все участники обмена, происшедшего после уравнительного распределения благ, распределение сложившееся после взаимовыгодного обмена, справедливым? Это зависит от условий обмена. Допустим, что между тремя участниками совместного хозяйства осуществлено уравнительное распределение созданных благ. Потребительские предпочтения индивидов I и II совершенно одинаковы, а вкусы индивида III отличаются от вкусов коллег. На этой основе между индивидами I и III возник взаимовыгодный обмен, в результате которого оба повысили свое благосостояние. Распределение, возникшее после обмена, не является справедливым, так как теперь индивид II, который не смог участвовать в обмене, завидует индивиду I. |
Однако, когда обмен совершается в условиях совершенной конкуренции, распределение возникшее после него является справедливым, если участники обмена признавали его справедливым до обмена.
Обозначим
количество благ, доставшееся трем
участникам совместного хозяйства в
результате уравнительного распределения,
вектором
![]() .
Поскольку распределение уравнительное,
то
.
Поскольку распределение уравнительное,
то![]() и
и![]() .
Пусть в этом хозяйстве существует
равновесная система ценРА,
РB,
по которым субъекты могут обмениваться
полученными в результате распределения
благами. Измеренные в этих ценах бюджеты
потребителей одинаковы.
.
Пусть в этом хозяйстве существует
равновесная система ценРА,
РB,
по которым субъекты могут обмениваться
полученными в результате распределения
благами. Измеренные в этих ценах бюджеты
потребителей одинаковы.
Обозначим
распределение, возникающее после
добровольного обмена между индивидами,
вектором
![]() .
В соответствии с первой теоремой
общественного благосостояния это
распределение является Парето-эффективным,
так как оно установилось в условиях
совершенной конкуренции. Докажем, что
это распределение является и справедливым.
.
В соответствии с первой теоремой
общественного благосостояния это
распределение является Парето-эффективным,
так как оно установилось в условиях
совершенной конкуренции. Докажем, что
это распределение является и справедливым.